最小生成树

Posted 2020-08-21 KennyRom

一、n个顶点的连通网络的最小生成树生成树有n个顶点，n-1条边

构造准则：

 - 尽可能使用网络中权值最小的边；

 - 必须使用且仅使用n-1条边来连接网络中的n个顶点；

 - 不能使用产生回路的边。

 

二、算法

1、prim算法

算法思想：

从连通网络N={V, E} 中的某一个顶点u0出发，选择与它关联的具有最小权值的边（u0,v），将其顶点加入到生成树的顶点集合U中。

以后每一步从一个顶点在U中，而另一个顶点不在U中的各条边种选择边权值最小的边（u,v），把改变加入到生成树的边集TE中，把它的顶点加入到集合U中。如此重复执行，直到网络中所有顶点都加入到生成树顶点集合U中为止。

 

进一步描述：

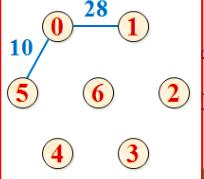
（1）在连通网的顶点集合V中，任选一个顶点，构成最小生成树的初始顶点集合U；

（2）在U和V-U 中各选一个顶点，使得该边的权值最小，把该边加入到最小生成树的边集TE中，同时将V-U中的该顶点并入到U中；

（3）反复执行第（2）步，直至V-U=ø为止。

 

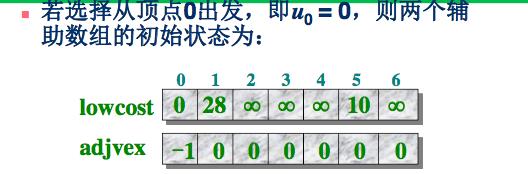
设置一个辅助数组closedge[]:

- lowcost域   存放生成树顶点集合内顶点到生成树外各顶点的各边上的当前最小的权值；

- adjvex域  记录生成树顶点集合外各顶点距离结合内哪个顶点最近（即权值最小）。

 

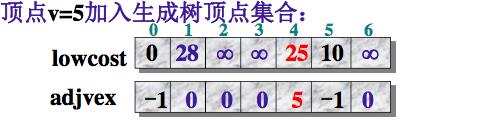
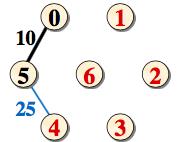
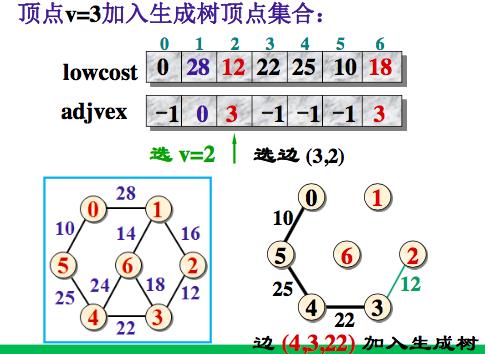
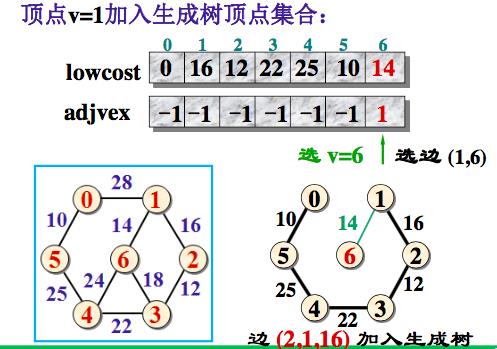
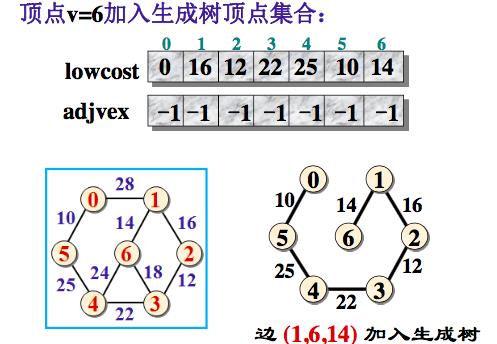
例子：

                                

 

 

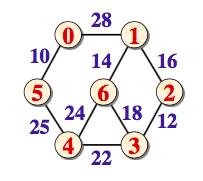
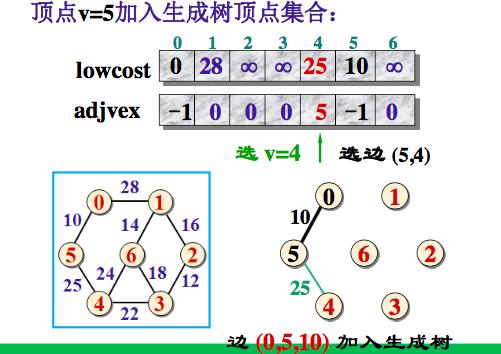
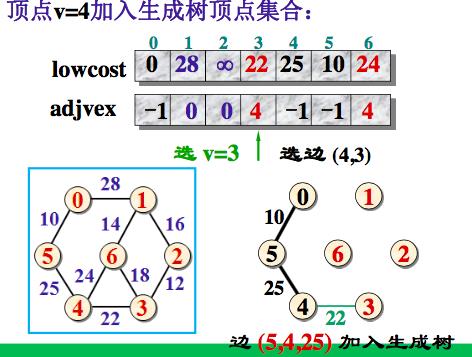
adjvex[v]为-1，表示它已经加入生成树顶点集合。

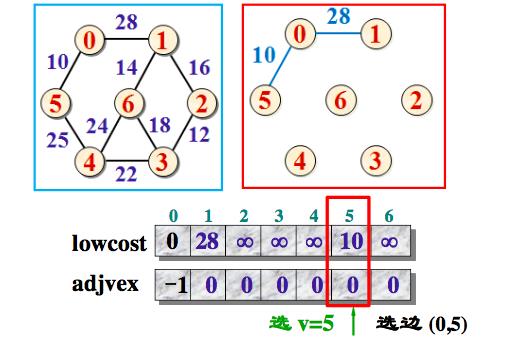
将边（adjvex[v], v, lowcost[v]) 加入生成树的边集合

取lowcost[i] = min{lowcost[i], Edge[v][i]}, 即用生成树顶点集合外个顶点i到刚加入该集合的新顶点v的距离Edge[v][i]与原来他们到生成树顶点集合中顶点的最短距离lowcost[i]做比较，取距离近的作为这些集合外顶点到生成树顶点集合内顶点的最短距离。

 

如果生成树顶点集合外顶点i到刚加入该集合的新顶点v的距离比原来它到生成树顶点集合中最短距离

还要近，则修改adjvex[i]：adjvex[i]=v. 表示生成树外顶点i到生成树内顶点v当前距离最近。

 

                      

 

 

 

 算法：

void Prim(Graph G, MST& T,int u)
{
	//从u点开始
	double * lowcost = new double[NumVertices];
	int *adjvex = new int[NumVertices];
	for(int i=0;i<NumVertices;i++)
	{
		lowcost[i]=G.Edge[u][i];  //所有结点到u的权值
		adjvex[i]=u;              //生成树顶点集合中只有u点
	}

	adjvex[u]=-1;    //u在生成树中，置为-1
	
	int k=0;

	//生成最小生成树
	for(int i=0;i<G.n;i++)
		if(i!=u)
		{
			EdgeDate min = MaxValue;   //找出最小边权
   			int v=0;                   //记录要加入的结点记号
			for(int j=0;j<NumVertices;j++)
				if(adjvex[j]!=-1 && lowcost[j]<min)
				{
					v=j;
					min=lowcost[j];
				}
			if(v)  //如果为0则找不到
			{//加入边
				T[k].tail=adjvex[v];
				T[k].head=v;
				T[k++].cost=lowcost[v];
				adjvex[v]=-1;
				for(int j=0;j<G.n;j++)  //修改
					if(adjvex[j]!=-1&&G.Edge[v][j]<lowcost[j])
					{
						lowcost[j]=G.Edge[v][j];
						adjvex[j]=v;
					}
			}
		}
}

　　

时间复杂度为O(n^2)，最小生成树不唯一

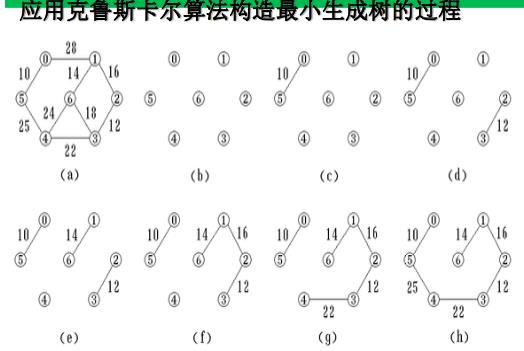
2、Kruskal算法

设有一个有n个顶点的连通网络N={V,E}, 最初先构造一个只有n个顶点，没有边的非连通图T={V,ø}，图中每个顶点自成一个连通分量。当在E中选到一条具有最小权值的边时，若改变的两个顶点落在不同的连通分量上，则将此边加入到T中；否则将此边舍去，重新选择一条权值最小的边，如此重复下去，直到所有顶点在同一个连通分量上为止。