c语言最小生成树
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了c语言最小生成树相关的知识,希望对你有一定的参考价值。
题目描述:给定一个地区的n个城市间的距离网,用Prim算法或Kruskal算法建立最小生成树,并计算得到的最小生成树的代价。
功能要求及说明:
(1)城市间的距离网采用邻接矩阵表示,邻接矩阵的存储结构定义采用课本中给出的定义,若两个城市之间不存在道路,则将相应边的权值设为自己定义的无穷大值。要求在屏幕上显示得到的最小生成树中包括了哪些城市间的道路,并显示得到的最小生成树的代价;
(2)表示城市间距离网的邻接矩阵(要求至少6个城市,10条边);并且利用文件对数据进行提取。
(3)输出最小生成树中包括的边及其权值,并显示得到的最小生成树的代价。
(4)采用模块化设计;
你自己改改吧。
#include <stdio.h>
#include <math.h>
struct point
double x,y;
;
struct distence
double _distence;
bool islink;
;
static double CaculateDistence(point x,point y)
return sqrt(pow((x.x-y.x),2.0)+pow((x.y-y.y),2.0));
static bool isInGroup(int *group,int value)
for(int i=0;i<10;++i)
if(value==group[i])return true;
return false;
int main()
/* 初始化各个点的值 */
point _point[10]=2.4169,8.2119,4.0391,0.1540,0.9645,0.4302,1.3197,1.6899,9.4205,6.4912,
9.5613,7.3172,5.7521,6.4775,0.5978,4.5092,2.3478,5.4701,3.5316,2.9632;
/* 初始化距离数组 */
distence _distence[10][10]=0.0,0;
////////////////////////////////////////////////////////////////
/* 计算距离 */
int i,j;
for (i=0;i<10;++i)
for(j=0;j<10;++j)
if(i==j)_distence[i][j]._distence=0;
else _distence[i][j]._distence=CaculateDistence(_point[i],_point[j]);
////////////////////////////////////////////////////////////////////
int pointgroup[10]=0;
int size=1;
pointgroup[0]=0;
///////////////////////////////////////////////////////////////
/* 计算最小生成树 */
for(;size<10;)
double dismin=32454.0;
int tmpx=0,tmpy=0;
for(i=0;i<size;++i)
for(j=0;j<10;++j)
if(_distence[pointgroup[i]][j].islink)continue;
else if(pointgroup[i]==j)continue;
else if(_distence[pointgroup[i]][j]._distence<dismin &&
!isInGroup(pointgroup,j))
dismin=
_distence[pointgroup[i]][j]._distence;
tmpx=pointgroup[i];
tmpy=j;
else continue;
_distence[tmpx][tmpy].islink=true;
_distence[tmpy][tmpx].islink=true;
pointgroup[size]=tmpy;
++size;
//////////////////////打印最小生成树//////////////////////////
for(i=0;i<10;++i)
for(int j=0;j<10;++j)
if(_distence[i][j].islink)printf("%d ------ %d\n",i,j);
return 0;
追问
你这也太简单了吧 算法呢
追答简单?最小生成树书上的核心算法也不过10几行吧。再自己添点不超过100行。
最小生成树的Prim算法以及Kruskal算法(C语言)
一、最小生成树
- 连通图的生成树是包含图中全部顶点的一个极小连通子图。
- 边尽可能的少,但要保持连通
- 若图中顶点数为n,则它的生成树含有 n-1 条边。对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路。

(一)最小生成树(最小代价树)
- 对于⼀个带权连通⽆向图G = (V, E),⽣成树不同,每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所有⽣成树的集合,若T为R中边的权值之和最⼩的⽣成树,则T称为G的最⼩⽣成树(Minimum-Spanning-Tree,MST)
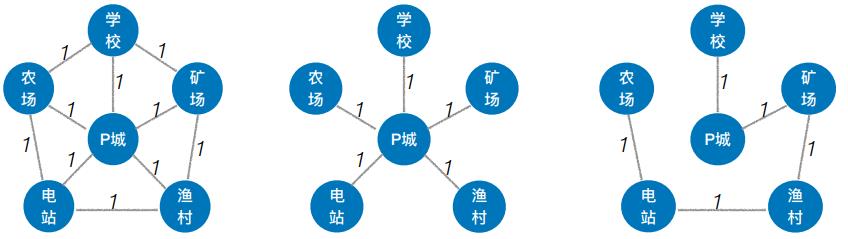
- 最小生成树可能有多个,但边的权值之和总是唯一且最小的
- 最小生成树的边数 = 顶点数 - 1。砍掉一条则不连通,增加一条边则会出现回路

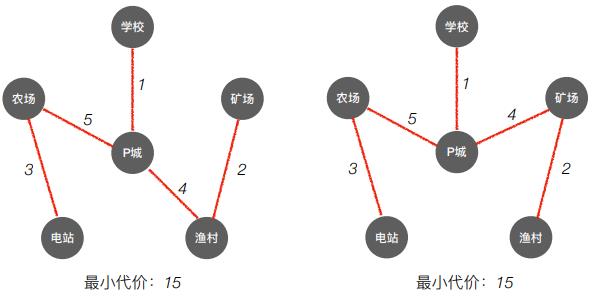
(二)Prim 算法(普里姆)
- Prim 算法(普里姆):从某一个顶点开始构建生成树;每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止。
- 从
P城开始进行建成生成树。

- 从
农场开始进行建成生成树。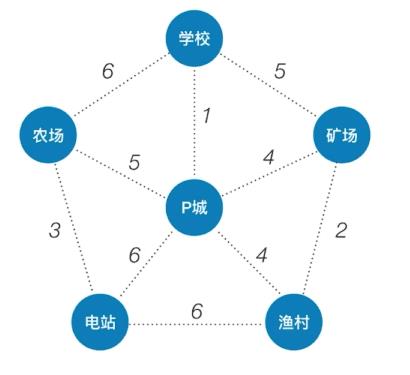
- 通过不同的结点开始,建成的最小生成树结构有可能不一样。
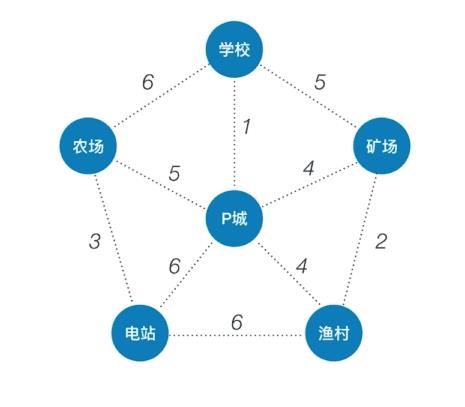
(三)Kruskal 算法(克鲁斯卡尔)
- Kruskal 算法(克鲁斯卡尔):每次选择⼀条权值最⼩的边,使这条边的两头连通(原本已经连通的就不选)直到所有结点都连通。
(四)Prim 算法 v.s. Kruskal 算法

1. Prim 算法的实现思想
- 初始:从V0开始
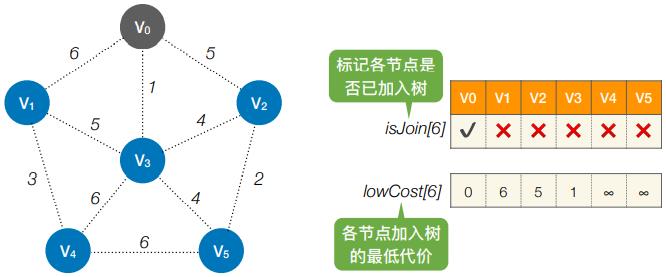
- 第1轮:循环遍历所有个结点,找到lowCost最低的,且还没加⼊树的顶点
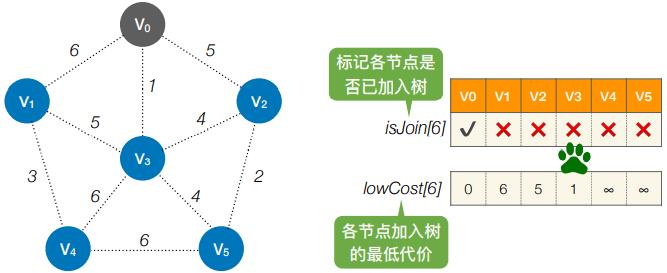
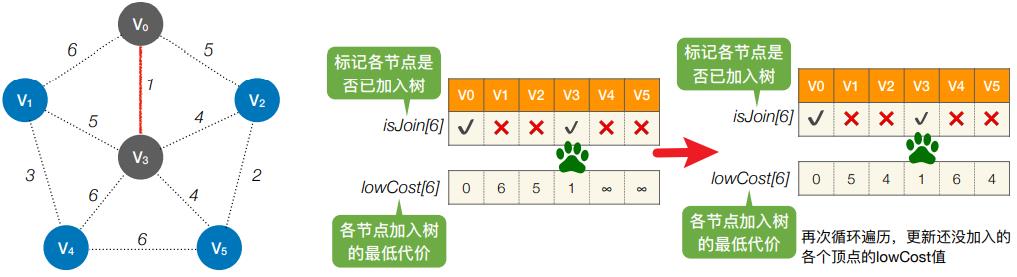
- 第2轮:循环遍历所有个结点,找到lowCost最低的,且还没加⼊树的顶点

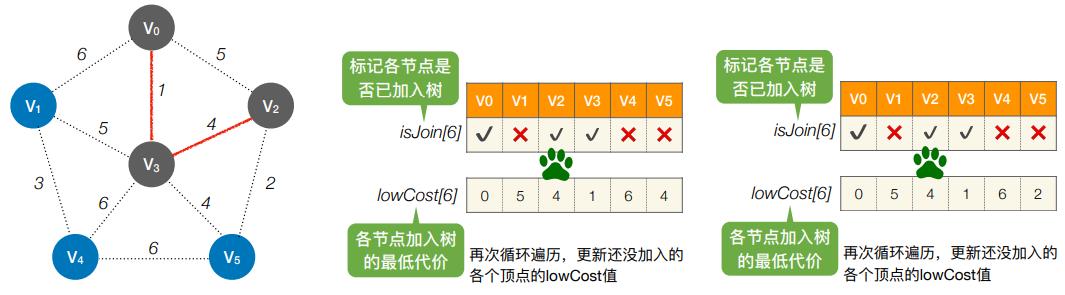
- 第3轮:循环遍历所有个结点,找到lowCost最低的,且还没加⼊树的顶点


- 第4轮:循环遍历所有个结点,找到lowCost最低的,且还没加⼊树的顶点
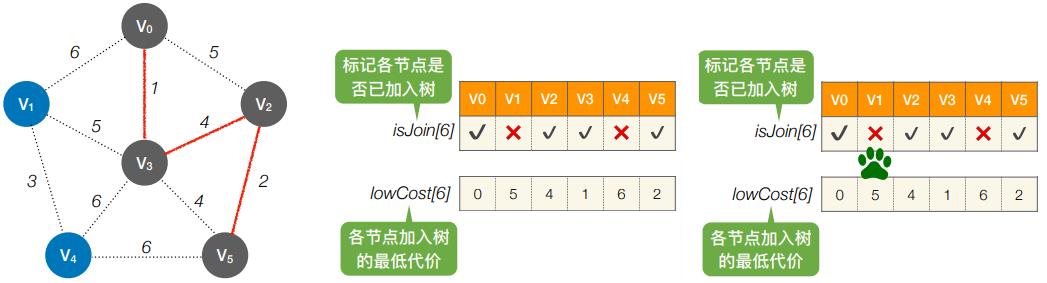
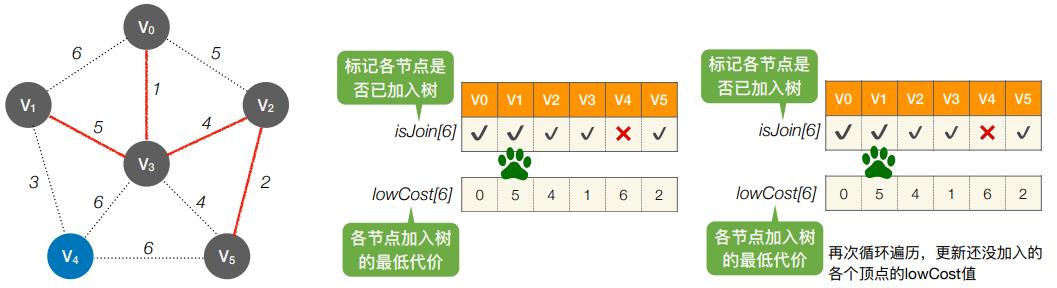

- 第5轮:循环遍历所有个结点,找到lowCost最低的,且还没加⼊树的顶点



2. Kruskal 算法的实现思想
- 初始:将各条边按权值排序
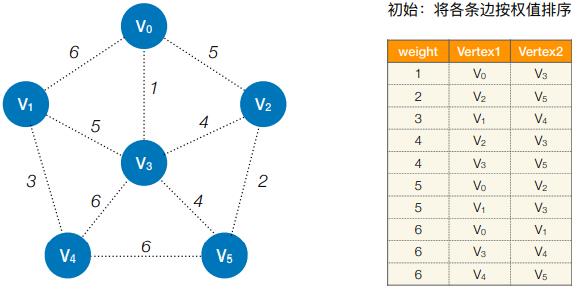
- 第1轮:检查第1条边的两个顶点是否连通(是否属于同⼀个集合)
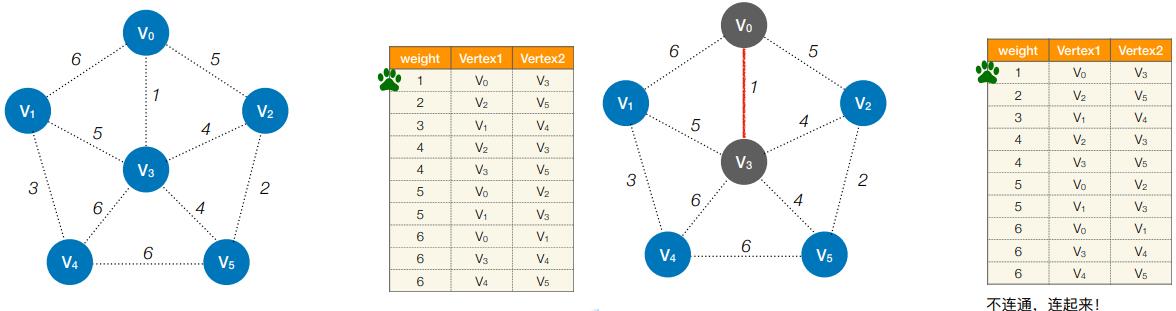
- 第2轮:检查第2条边的两个顶点是否连通(是否属于同⼀个集合)

- 第3轮:检查第3条边的两个顶点是否连通(是否属于同⼀个集合)
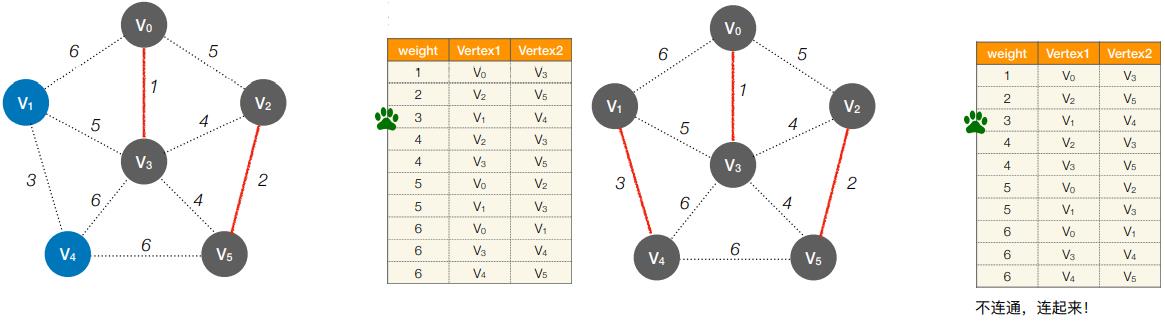
- 第4轮:检查第4条边的两个顶点是否连通(是否属于同⼀个集合)
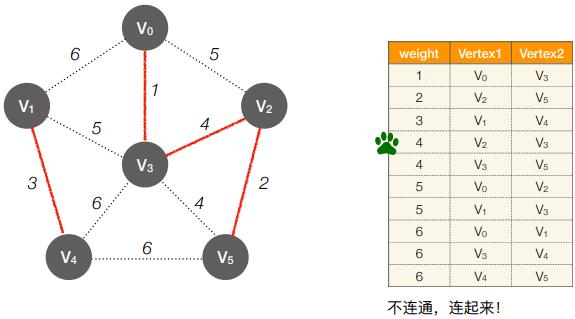
- 第5轮:检查第5条边的两个顶点是否连通(是否属于同⼀个集合)

- 第6轮:检查第6条边的两个顶点是否连通(是否属于同⼀个集合)

- 共执⾏ e 轮,每轮判断两个顶点是否属于同⼀集合,需要 O(log2e)总时间复杂度 O(elog2e)
以上是关于c语言最小生成树的主要内容,如果未能解决你的问题,请参考以下文章