图像处理分析与机器视觉读书笔记-------第二章图像及其表达与性质

Posted 2020-08-21 有梦放飞

2.1 图像表达若干概念

      图像和信号常用数学模型来描述。

连续图像函数

     图像函数的值对应于图像点的亮度。人类眼睛视网膜或者TV摄像传感器上的图像本身是两维的（2D）。我们将这种记录了明亮度信息对的图像称为亮度图像。2D亮度图像是3D场景的透视投影。

     图像处理通常考虑的是静态图像，时间t作为常量。单色的静态图像是用连续的图像函数f(x,y)来表示的，其中的变量是平面的两个坐标。计算机化的图像处理使用的数字图像函数通常表示成矩阵的形式，因此其坐标是整数。图像函数的定义域是平面的一个区域R

R={(x,y),1<=x<=x_m,1<=y<=y_n}

其中x_m，yn表示最大的图像坐标。习惯上采用的图像坐标方向是普通的笛卡尔形式（横轴x，纵轴y，左下原点）

     图像函数的值域是有限的，在单色图像中最低值对应于黑，而最高值对应于白，在它们之间的亮度值是灰阶。

     数字图像的品质随空间、频谱、辐射计量、时间分辨率增长而提高。空间分辨率是由图像平面上图像采样点间的接近程度确定的，频谱分辨率是由传感器获得的光线频率带宽决定的，辐射计量分辨率对应于可区分的灰阶数量，时间分辨率取决于图像获取的时间采样间隔。

2.2图像数字化

     数字图像化是指将连续函数f(x,y)采样为一个M行N列的矩阵。图像量化给每个连续的样本数值一个整数数字，图像函数f(x,y)的连续范围被划分为K个区间。采样及量化越精细（即M,N,K越大），对连续函数f(x,y)的近似就越好。

     图像函数采样有两个问题，其一是确定采样的间隔，即相邻两个采样图像点的距离，其二是设置采样点的几何排列（采样栅格）。

2.2.1采样

     一个连续图像在采样点处被数字化，这些采样点是在平面上排列的，称它们的几何关系为栅格。因此数字图像是一个数据结构，通常是矩阵。在实践中，栅格一般是方的或者是正六边形的。

    栅格中一个无限小的采样点对应于数字化图像的一个像元，也称作像素或图像元素。

 

2.2.2量化

    在图像处理中，采样的图像数值fs（jΔx,kΔy）用一个数字来表示。将图像函数的连续数值（亮度）转变为其数字等价量的过程是量化(quantization)。

    大部分数字图像处理仪器都采用k个等间隔的量化方式。如果用b位来表示像素亮度的数值，那么亮度阶就是k=2^b.

    在量化级别不够时，图像的主要问题时出现伪轮廓。

2.3数字图像性质

2.3.1数字图像的度量和拓扑性质

     一幅数字图像由有限大小的像素组成，像素反映图像特定位置处的亮度信息。

     满足以下三个条件的任何函数是一种“距离”（或度量）：

D（p,q）>=0,当且仅当p=q时D（p,q）=0  同一性

D（p,q）=D（q,p）                               对称性

      D（p,r）<=D（p,q）+D（q,r）                三角不等式

     坐标为（i,j）和（h,k）的两点间的距离可以定义为几种形式。这里介绍欧式距离、“城市街区”距离、“棋盘”距离。

     欧式距离：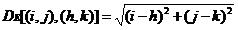

     两点间的距离也可以表示为数字栅格上从起点移动到终点所需的最少的基本步数。如果只允许横向和纵向的移动，就是距离D_4。D4也称为“城市街区”距离。

D₄[(i,j),(h,k)]=|i-h|+|j-k|

     在数字栅格中如果允许对角线方向的移动，就得到D₈。称为“棋盘”距离。D₈[(i,j),(h,k)]=max{|i-h|，|j-k|}

     像素邻接性：任何两个像素如果它们之间的距离D₄=1，则称彼此是4-邻接（4-neighbors）。8-邻接是指两个像素之间的距离D₈=1。

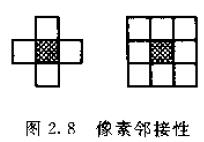
    由一些彼此邻接的像素组成的重要集合，称为区域。如果两个像素之间存在一条路径，那么这些像素就是连通的。如果区域中没有孔，称为简单连通区域；有孔的区域称为复连通。

    边缘：是一个像素和其直接邻域的局部性质，它是一个有大小和方向的矢量。边缘告诉我们在一个像素的小邻域内图像亮度变化有多快。边缘计算的对象是具有很多亮度级别的图像，计算边缘的方式是计算图像函数的梯度，边缘的方向与梯度的反向垂直，梯度方向指向函数增长的方向。

    区域的形状可以用是否具有凸性来定性的描述。如果区域内的任意两点连成一条线而这条线完整地位于区域内，我们就称该区域是凸的。凸性将所有区域划分为两个等价类：凸的和非凸的。

2.3.2直方图

     图像的亮度直方图hf(z)给出图像中亮度值z出现的频率。数字图像的直方图一般都有很多极小和极大值，可通对直方图进行局部平滑。如可以用相邻直方图元素的局部平均来做，因此新的直方图按下式进行计算：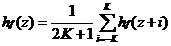

其中K是一个常量，代表平滑所使用的邻域的大小。

2.3.3熵（Entrony）

     如果知道概率密度p，用熵H就可以估计出图像的信息量。

     假设离散随机变量X的可能结果（也称作状态）是x₁,...,x_n，设p(x_k)是出现x_k（k=1,...,n）的概率，熵定义为

2.3.4图像的视觉感知

     事实上，人的感知敏感度大致上是与输入信号的轻度成对数关系的，在这种情况下，经过一个初始的对数变换，复合激励的响应可以作为线性的看待。

     对比度（contrast）

对比度是亮度的局部变化，定义为物体亮度的平均值与背景亮度的比值。表观上的亮度很大程度上取决于局部背景的亮度，这种现象被称为条件对比度。

     敏锐度（acuity）

敏锐度是觉察图像细节的能力。

2.3.5图像中的噪声

     实际的图像常受一些随机误差的影响而退化，称为噪声。噪声一般由其概率特征来刻画。理想的噪声，称为白噪声。其一个特例是高斯噪声。

     当图像通过信道传输时，噪声一般与出现的图像信号无关，这种独立于信号的退化被称为加性噪声。模型为f(x,y)=g(x,y)+v(x,y)

     乘性噪声：f=gv

     量化噪声：在量化级别不足时出现。

     冲击噪声：是指一幅图像被个别噪声像素破坏，这些像素的亮度与其邻域的显著不同。胡椒盐噪声是指饱和的冲击噪声，这时图像被一些白的或黑的像素所破坏。胡椒盐噪声会使二值图像退化。