树的插入删除旋转归纳

Posted 2020-08-21 Leo_wlCnBlogs

AVL 树的插入、删除、旋转归纳

参考链接：

http://blog.csdn.net/gabriel1026/article/details/6311339

 

1126号注：先前有一个概念搞混了：

　　节点的深度 Depth 是指从根节点到当前节点的长度；

　　节点的高度 Height 是指从当前节点向下，到子孙中所有叶子节点的长度的最大值。

 

 

之前简单了解过 AVL 树，知道概念但一直没动手实践过。Now

 

 AVL 树是二叉搜索树的一种。二叉搜索树的规则就是：每个节点的 left child 都比自己小，right child 都比自己大。而 AVL 的在此之上又加了一个规则：每个节点的 left 深度与 right 深度只差<=1，这样就能充分利用 二叉树的结构，避免出现一个分支走到黑，导致搜索效率变低。如下图：

                                             

                                这种树结构，搜索起来完全没有体现出二叉搜索树的优势

 

所以同样多的元素，搜索树的深度越低，就会越快的定位到搜索点。

 

AVL 树为了保持树的平衡，每次插入、删除都会检查 每个受影响的节点，深度差是否 <  1。最难的部分就是如果树失衡，如何调整节点。插入的处理流程大致如下：

     给定一个 value，一路比较直到插入到某个位置。然后查找哪些节点因此而失衡，针对第一个失衡的节点进行旋转。

 

下面是我从另一个博客上找来的图（http://blog.csdn.net/gabriel1026/article/details/6311339），介绍了四种失衡的情况，以及调整方式：

注：图中红色的小块 表示新插入的元素，A 点表示从插入点向上，发现的第一个失衡的点。

 

      AVL树的旋转一共有四种情形，注意所有旋转情况都是围绕着使得二叉树不平衡的第一个节点展开的。

1： 

     

     图中在 Bl 下新插入一个子节点，导致 A 左侧深度为 3，右侧为 1，失衡。右旋。

2：

     

3：

     

 

4：

 

不知道大家看明白了调整的规则吗？

如果您看明白了，你真是大牛！！！

没看图之前我大致明白了四种调整规则，看了后两幅图片之后，彻底迷糊了。完全不知道如何用程序来表示四种规则，也不知道怎么从一棵树中提取到这四个特征。。。后两张图折磨了我一天多，才发现：后两张图应该是存在逻辑错误的。。。

     AVL 树每次插入之前，以及插入之后，都应该是平衡的。而 图3 和图4，插入之前就不平衡：拿图三来说：插入之前，A 的 left 深度为3，right 深度为 1，本身就有问题

 

 

虽然上面的图有问题，但是介绍的思路是非常正确的，只是检查到底符合 LL、RR、LR、RL 中哪个特征时，被带跑偏了。

所以明白了这四种调整方式后，下一步就是用程序的思维，检查何时用哪种规则了。这一点我认为网上的博客介绍的也不太详细，我这理解力一般的人，看过教程后，实现起来依旧是一团麻。下面是我用到的插入流程：

     1：拿到新节点 newNode，根据左小右大的二叉搜索树规则，一路定位到一个具体的节点 currNode，把 newNode 当成 currNode 的 child 插入到树中。（不用记录 newNode 是 currNode 的 left 还是 right ）

     2：检查 currNode 是否失衡，如果没有失衡，就检查 currNode 的 parent，不失衡就在检查 parent 的 parent….. 这样直到拿到一个失衡节点（如果直到根节点依旧平衡，那当前树就不用做任何调整），把失衡点当成 currNode

     3：关键点的平衡来了：

          如果 Depth(currNode.left) - Depth(currNode.right) = 2：说明左侧深度大于右侧深度，可能是 LL、LR 中的一种：此时检查 newNode 和 currNode、currNode.left 的大小关系

               1）如果 newNode 比 currNode 小，并且 newNode 比 currNode.left 小，此时符合 LL：对 currNode 右旋；

               2）如果 newNode 比 currNode 小，但是 newNode 比 currNode.left 大，此时符合 LR：先对 currNode.left 左旋，然后对 currNode 右旋；

          如果 Depth(currNode.right) - Depth(currNode.left) = 2：说明右侧深度大于左侧深度，可能是 RR、RL 中的一种：此时检查 newNode 和 currNode、currNode.right 的大小关系：

               1）如果 newNode 比 currNode 大，并且 newNode 比 currNode.right 大，符合 RR，对 currNode 左旋；

               2）如果 newNode 比 currNode 大，并且 newNode 比 currNode.right 小，符合 RL：先对 currNode.right 右旋，然后对 currNode 左旋；

插入、调整结束。

 

中间有几个容易混的地方。这样叙述起来，用程序实现就很方便了。剩下的就是 左旋、右旋的函数实现，这两个函数需要特别小心，每个节点的 parent、left、right 都要很小心的处理。基本上包含四个函数：

     insert 负责执行 1

     balance 负责执行 2、3、4

     leftRotate、rightRotate 函数用来实现旋转。

代码我在最后统一贴出来。

 

 

 

插入搞定了，还有删除操作：删除的流程如下：

     1：拿到要删除的数字 value，从根节点开始比对，知道找到一个要删除的节点：currNode （没找到正好不用删了 →_→）

     2：从左子树中找到一个最大值（左子树中的值都比 currNode 小）：targetNode（如果左子树为空，那就直接把 right 节点上位；如果 right 也是空的，那就直接删掉 currNode 就好了）

     3：把 targetNode 放到 currNode 的位置上：因为每个 节点都有 parent、left、right 三个关联点，要仔细处理（错误了好几次才正确→_→）

     4：和 插入类似，从 targetNode 开始一路向上，找到第一个失衡点。此时只有 LL 和 RR 两种失衡情况，判断起来相对容易些

 

 

AVL 树最基本的插入和删除就是这样了。插入删除过程中，具体为什么旋转、为什么使用这种规则，是否覆盖到了所有的特例等问题，都是有规律可以归纳的。对这些规律我还比较模糊，知其然不知其所以然。。。树是一个很神奇的数据结构，诸多奇思妙想都能用树结构来实现，还要多想想树的规律。

 

JS 代码如下：

 

 

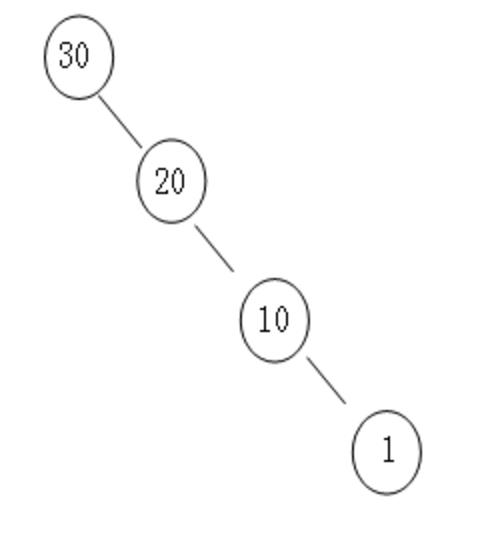
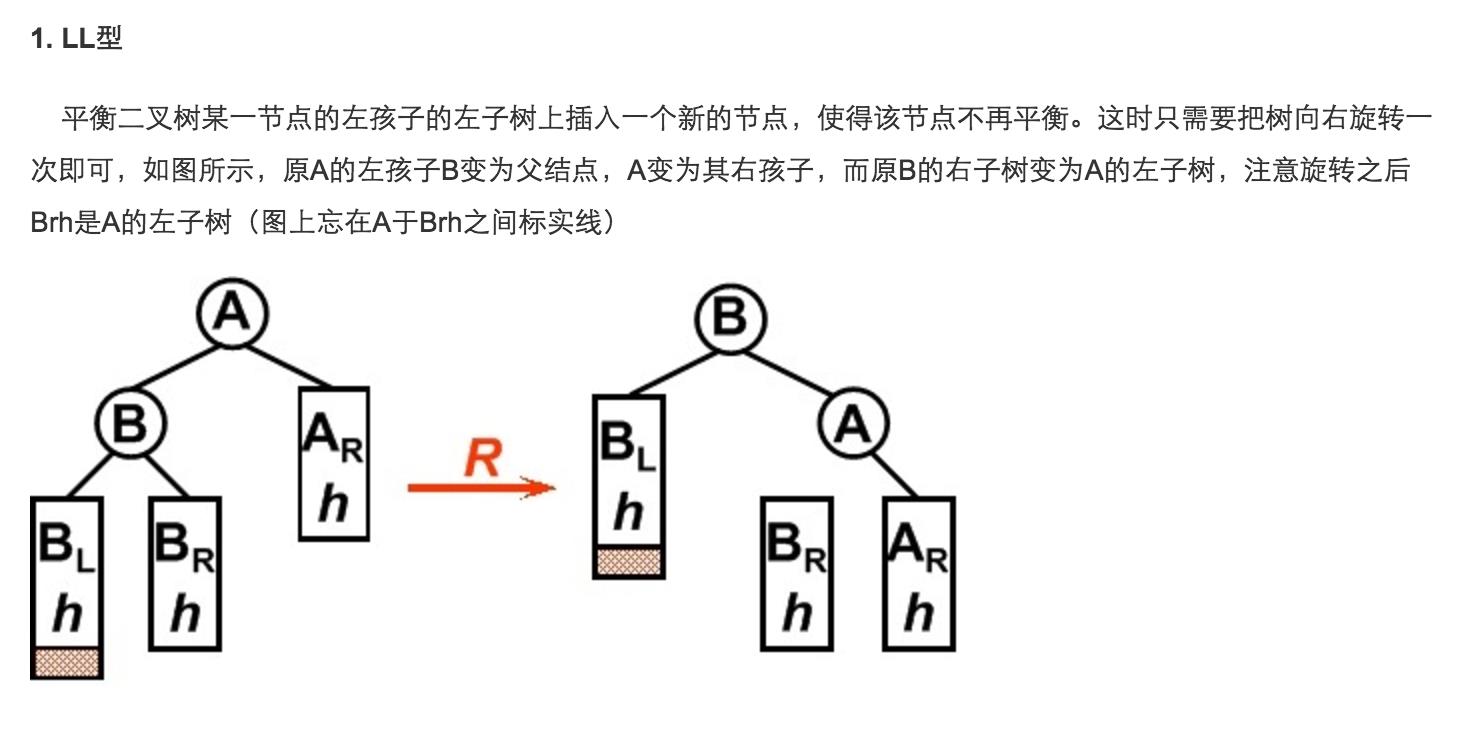
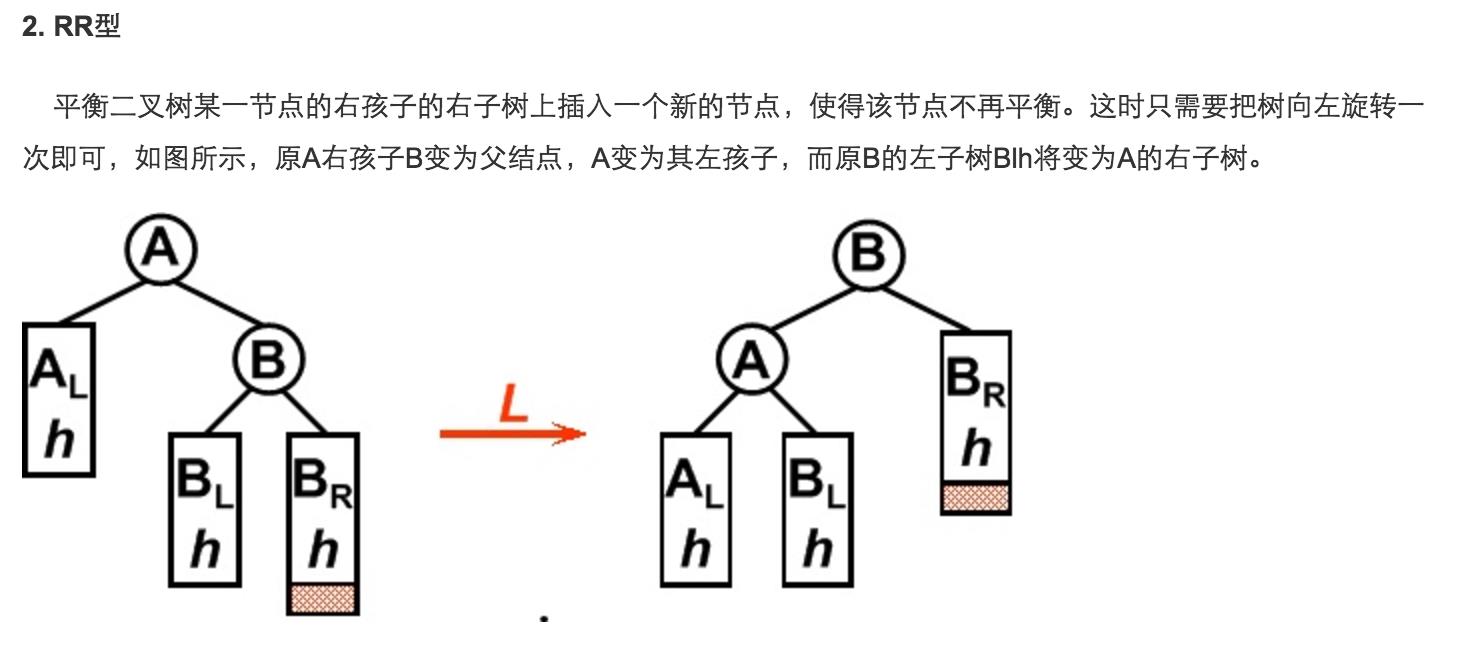
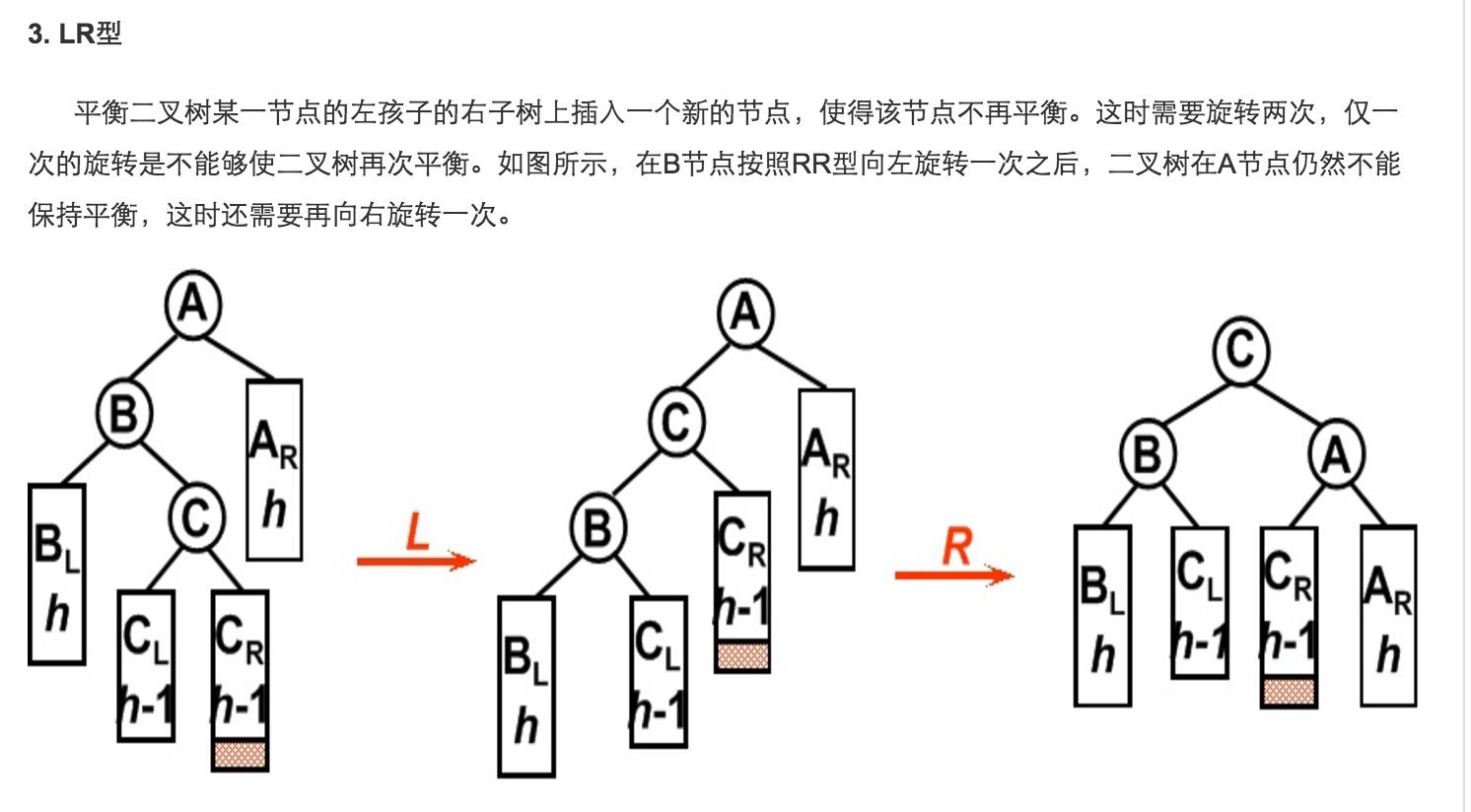
 View Code

/**
* Created by CG on 16/11/20.
*/

 

var TreeNode = function(){
this.parent = null;
this.left = null;
this.right = null;

this.value = null;
};

var AVLTree = {

insert : function (value) {
this.log("新加节点:new add: " + value);
if(this._tree == null){
var node = new TreeNode();
node.value = value;
this._tree = node;
return;
}

var newNode = new TreeNode();
newNode.value = value;

var currNode = this._tree;
while(true){
if(currNode == null){
this.log(" ======== currNode: null");
return;
}

//走向左子树
if(value <= currNode.value){
this.log(" to left: value: " + value + " currValue: " + currNode.value);
if(currNode.left){
currNode = currNode.left;
continue;
}
else {
newNode.parent = currNode;
currNode.left = newNode;
this.balanceTree(currNode, newNode);
break;
}
}
//走向右子树
else {
this.log(" to right: value: " + value + " currValue: " + currNode.value);
if(currNode.right){
currNode = currNode.right;
continue;
}
else {
newNode.parent = currNode;
currNode.right = newNode;
this.balanceTree(currNode, newNode);
break;
}
}
}
},
balanceTree : function (currNode, newNode) {
if(!currNode){
return;
}

this.printTreeByLevel();
while(currNode){
this.log("---------===========--- check if adjust: " + currNode.value);
if(currNode.parent){
this.log(" parent: " + currNode.parent.value);
}
var leftDepth = this.calcuDepth(currNode.left);
var rightDepth = this.calcuDepth(currNode.right);
this.log("leftDepth: " + leftDepth + " rightDepth: " + rightDepth);
if(leftDepth - rightDepth == 2){
if(newNode == null){
this.rightRotate(currNode);
}
else if(newNode.value < currNode.value && newNode.value < currNode.left.value){
this.log("LL");
this.rightRotate(currNode);
}
else if(newNode.value < currNode.value && newNode.value > currNode.left.value){
this.log("LR");
this.leftRotate(currNode.left);
this.rightRotate(currNode);
}
}
else if(rightDepth - leftDepth == 2){
if(newNode == null){
this.leftRotate(currNode);
}
else if(newNode.value > currNode.value && newNode.value > currNode.right.value){
this.log("RR");
this.leftRotate(currNode);
}
else if(newNode.value > currNode.value && newNode.value < currNode.right.value){
this.log("RL");
this.rightRotate(currNode.right);
this.leftRotate(currNode);
}
}

currNode = currNode.parent;
this.printTreeByLevel();
}
},
leftRotate : function (currNode) {
this.log("leftRotate: " + currNode.value);
var oldRight = currNode.right;

//如果当前节点就是根节点，更新外界引用的根节点
if(currNode == this._tree){
this._tree = oldRight;
}
else {
//更新变动前的 currNode 的 parent 的指向
if(currNode.parent.left == currNode){
currNode.parent.left = oldRight;
}
else if(currNode.parent.right == currNode){
currNode.parent.right = oldRight;
}
}

//更新 curr 和 oldRight 的 parent
oldRight.parent = currNode.parent;

//更新 curr 和 oldRight 的 child
currNode.right = oldRight.left;
if(oldRight.left){
oldRight.left.parent = currNode;
}

oldRight.left = currNode;
currNode.parent = oldRight;

this._tree.parent = null;
return oldRight;
},
rightRotate : function (currNode) {
this.log("rightRotate: " + currNode.value);
var oldLeft = currNode.left;

//如果当前节点就是根节点，更新外界引用的根节点
if(currNode == this._tree){
this._tree = oldLeft;
}
else {
//更新变动前的 currNode 的 parent 的指向
if(currNode.parent.left == currNode){
currNode.parent.left = oldLeft;
}
else if(currNode.parent.right == currNode){
currNode.parent.right = oldLeft;
}
}

//更新 curr 和 oldLeft 的 parent
oldLeft.parent = currNode.parent;

//更新 curr 和 oldLeft 的 child
currNode.left = oldLeft.right;
if(oldLeft.right){
oldLeft.right.parent = currNode;
}

oldLeft.right = currNode;
currNode.parent = oldLeft;

this._tree.parent = null;
return oldLeft;
},

/**
* 计算左右节点的深度。叶子节点的深度都是 1，依次向上加 1
* @param treeNode
* @returns {number}
*/
calcuDepth : function (treeNode) {
if(!treeNode){
return 0;
}
if(treeNode.left == null && treeNode.right == null){
return 1;
}
return 1 + Math.max(this.calcuDepth(treeNode.left), this.calcuDepth(treeNode.right));
},

/**
* 从树中删除一个节点
* @param value
*/
remove : function (value) {
this.log(" ===== 将要删除元素：" + value);
if(!value){
return;
}

//定位到节点
var currNode = this._tree;
while(currNode){
if(currNode.value == value){
break;
}
currNode = value > currNode.value ? currNode.right : currNode.left;
}
if(currNode.value != value){
this.log("没找到啊");
return;
}

var targetNode = null;
//删除该节点
if(currNode.left){
//有左子树，找到其中最大值来替代空位
targetNode = this.findMaxNode(currNode.left);
this.log(" == currNode.left: " + targetNode.value);

//更新 target 父节点的 child 指向
if(targetNode.parent != currNode){
var newChild = targetNode.left ? targetNode.left : targetNode.right;
if(targetNode.parent.left == targetNode){
targetNode.parent.left = newChild;
}
else {
targetNode.parent.right = newChild;
}
}
//更新 target 的 parent 指向
targetNode.parent = currNode.parent;

// 更新 target 的 right 指向
targetNode.right = currNode.right;
if(currNode.right){
currNode.right.parent = targetNode;
}
// 更新 target 的 left 指向 、、一定要注意避免自身死循环
if(currNode.left != targetNode){
targetNode.left = currNode.left;
currNode.left.parent = targetNode;
}
}
//没有左子树，但是有右子树，直接把右子树提上去就好了
else if(currNode.right){
targetNode = currNode.right;
targetNode.parent = currNode.parent;
this.log(" == currNode.right: " + targetNode.value);
}
//如果 curr 是叶子节点，只要更新 curr 的 parent 就可以了，没有额外处理

//更新 curr 父节点的 child 指向
if(currNode.parent && currNode.parent.left == currNode){
currNode.parent.left = targetNode;
}
else if(currNode.parent && currNode.parent.right == currNode){
currNode.parent.right = targetNode;
}
else {
this._tree = targetNode; //说明是 根节点
}

this.log(" +++++++++++++ ");
this.printTreeByLevel();
this.balanceTree(targetNode == null ? currNode.parent : targetNode);
this.log(" +++++++++++++ ");
},

findMaxNode : function(treeNode){
while(treeNode){
if(treeNode.right){
treeNode = treeNode.right;
}
else {
return treeNode;
}
}
return treeNode;
},

 

log : function (str) {
console.log(str);
},
/**
* 按照层级打印一棵树的各层节点名字
**/
printTreeByLevel : function () {
this.log("-----------------------");
if(!this._tree){
this.log(" === empty ===");
return;
}
var nodeList = [];
nodeList.push(this._tree);
while(nodeList.length > 0){
var len = nodeList.length;
var value = "";
for(var i=0; i<len; ++i){
var currNode = nodeList[i];
value += currNode.value + " ";
if(currNode.left){
nodeList.push(currNode.left);
}
if(currNode.right){
nodeList.push(currNode.right);
}
}
this.log(value);

nodeList = nodeList.slice(len);
}
},
};

AVLTree.printTreeByLevel();
AVLTree.log("====================================================================================================");
var list = [3,7,9,23,45, 1,5,14,25,24, 13,11, 26];
for(var index in list){
AVLTree.insert(list[index]);
}
AVLTree.log("====================================================================================================");
AVLTree.printTreeByLevel();
// AVLTree.remove(1);
// AVLTree.remove(25);
// AVLTree.printTreeByLevel();

 

 

 

 

 

分类: 数据结构