转载编辑距离及编辑距离算法

Posted 2020-08-21 波比12

转载在：http://www.cnblogs.com/biyeymyhjob/archive/2012/09/28/2707343.html

编辑距离概念描述：

编辑距离，又称Levenshtein距离，是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

例如将kitten一字转成sitting：

1. sitten （k→s）
2. sittin （e→i）
3. sitting （→g）

俄罗斯科学家Vladimir Levenshtein在1965年提出这个概念。

 

问题：找出字符串的编辑距离，即把一个字符串s1最少经过多少步操作变成编程字符串s2，操作有三种，添加一个字符，删除一个字符，修改一个字符

 

解析：

首先定义这样一个函数——edit(i, j)，它表示第一个字符串的长度为i的子串到第二个字符串的长度为j的子串的编辑距离。

显然可以有如下动态规划公式：

• if i == 0 且 j == 0，edit(i, j) = 0
• if i == 0 且 j > 0，edit(i, j) = j
• if i > 0 且j == 0，edit(i, j) = i
• if i ≥ 1  且 j ≥ 1 ，edit(i, j) == min{ edit(i-1, j) + 1, edit(i, j-1) + 1, edit(i-1, j-1) + f(i, j) }，当第一个字符串的第i个字符不等于第二个字符串的第j个字符时，f(i, j) = 1；否则，f(i, j) = 0。

 

 

	0	f	a	i	l	i	n	g
0
s
a
i
l
n

 

 

	0	f	a	i	l	i	n	g
0	0	1	2	3	4	5	6	7
s	1
a	2
i	3
l	4
n	5

 计算edit(1, 1)，edit(0, 1) + 1 == 2，edit(1, 0) + 1 == 2，edit(0, 0) + f(1, 1) == 0 + 1 == 1，min(edit(0, 1)，edit(1, 0)，edit(0, 0) + f(1, 1))==1，因此edit(1, 1) == 1。 依次类推：

	0	f	a	i	l	i	n	g
0	0	1	2	3	4	5	6	7
s	1	1	2	3	4	5	6	7
a	2	2
i	3
l	4
n	5

edit(2, 1) + 1 == 3，edit(1, 2) + 1 == 3，edit(1, 1) + f(2, 2) == 1 + 0 == 1，其中s1[2] == \'a\' 而 s2[1] == \'f\'‘，两者不相同，所以交换相邻字符的操作不计入比较最小数中计算。以此计算，得出最后矩阵为：

	0	f	a	i	l	i	n	g
0	0	1	2	3	4	5	6	7
s	1	1	2	3	4	5	6	7
a	2	2	1	2	3	4	5	6
i	3	3	2	1	2	3	4	5
l	4	4	3	2	1	2	3	4
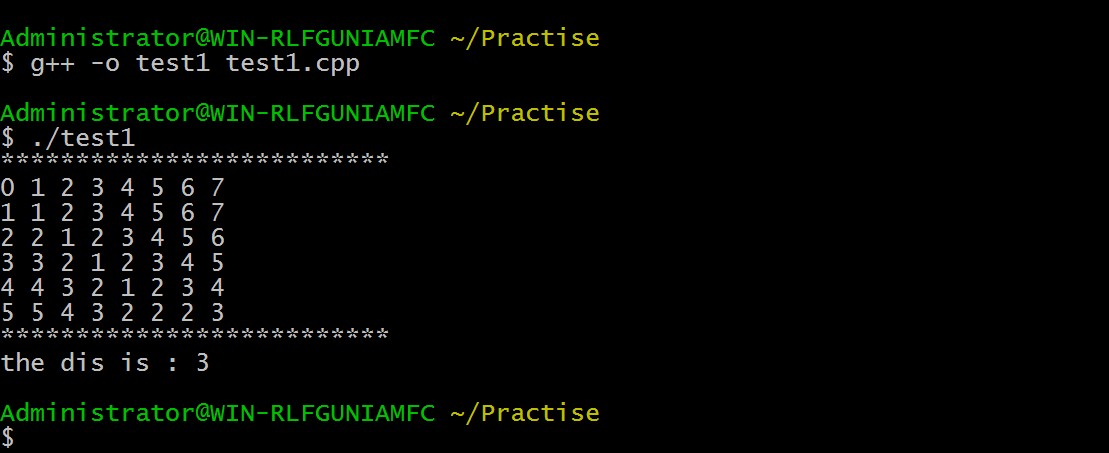
n	5	5	4	3	2	2	2	3

 

程序（C++）：注意二维数组动态分配和释放的方法！！

#include <iostream>
#include <string>

using namespace std;

int min(int a, int b)
{
    return a < b ? a : b;
}

int edit(string str1, string str2)
{
    int max1 = str1.size();
    int max2 = str2.size();

    int **ptr = new int*[max1 + 1];
    for(int i = 0; i < max1 + 1 ;i++)
    {
        ptr[i] = new int[max2 + 1];
    }

    for(int i = 0 ;i < max1 + 1 ;i++)
    {
        ptr[i][0] = i;
    }

    for(int i = 0 ;i < max2 + 1;i++)
    {
        ptr[0][i] = i;
    }

    for(int i = 1 ;i < max1 + 1 ;i++)
    {
        for(int j = 1 ;j< max2 + 1; j++)
        {
            int d;
            int temp = min(ptr[i-1][j] + 1, ptr[i][j-1] + 1);
            if(str1[i-1] == str2[j-1])
            {
                d = 0 ;
            }
            else
            {
                d = 1 ;
            }
            ptr[i][j] = min(temp, ptr[i-1][j-1] + d);
        }
    }

    cout << "**************************" << endl;
    for(int i = 0 ;i < max1 + 1 ;i++)
    {
        for(int j = 0; j< max2 + 1; j++)
        {
            cout << ptr[i][j] << " " ;
        }
        cout << endl;
    }
    cout << "**************************" << endl;
    int dis = ptr[max1][max2];

    for(int i = 0; i < max1 + 1; i++)
    {
        delete[] ptr[i];
        ptr[i] = NULL;
    }

    delete[] ptr;
    ptr = NULL;

    return dis;
}

int main(void)
{
    string str1 = "sailn";
    string str2 = "failing";

    int r = edit(str1, str2);
    cout << "the dis is : " << r << endl;

    return 0;
}

执行效果：