谈谈四元数

Posted 2020-08-19 艾攀

　　作为从未学过惯性导航的小白，四元数折磨了我很长时间，至今也是似懂非懂的。下面说的不正确的，希望大神指点。

　　四元数说起来很好理解，即表示绕着瞬时轴n旋转θ角度。瞬时轴n=cosαi+cosγj+cosβk。

　　四元数的表示即Q=cos(θ/2)+sin(θ/2)(cosαi+cosγj+cosβk)=q0+q1i+q2j+q3k。姿态矩阵是如何和四元数对应的呢？θ和n是多少呢？

　　先摆出一个很重要的性质：坐标系旋转，矢量固定不变。坐标系OXYZ按照四元数Q转动，得到新坐标系OXbYbZb，设矢量V在两坐标系中的坐标分别为Ve，Vb。那么有，Vb=Q^-1VeQ。具体见http://www.doc88.com/p-893241688972.html

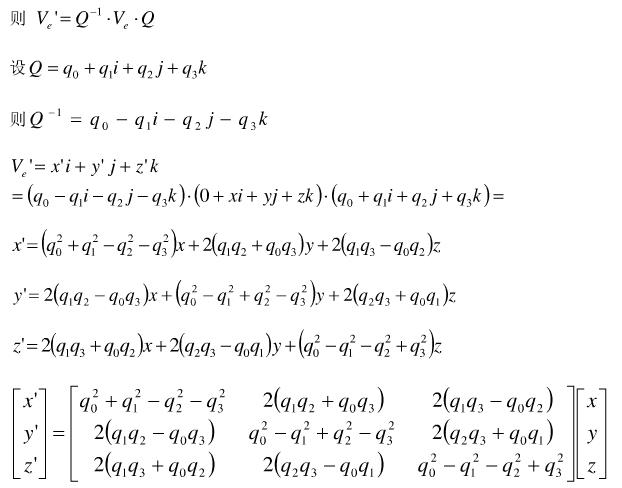
这就是四元数得到旋转矩阵的由来。

这篇文章写的太好了，我就直接复制过来了，感谢作者。

四元数表示旋转矩阵，四元数的微分都说的很清楚了，然而我还是不知道q0,q1,q2,q3跟姿态角到底有什么关系。我想了很久，不知道下面的理解是不是对的。

n的方向就是陀螺仪测得的（wx,wy,wz）矢量和的方向，θ就是（wx,wy,wz）矢量和的长度！！！

wx,wy,wz是飞机绕三个轴旋转的角速度，飞机我们认为是分步骤绕三个轴旋转后到达最终位置的，四元数旋转我们认为是一步旋转到最终位置的。那么这两种旋转肯定有关系啊！四元数是绕一个向量旋转，n表示的是旋转方向，θ表示的是旋转量。wx,wy,wz的旋转其实也是绕三个向量旋转，即（wx,0,0）（0,wy,0）（0,0,wz）。它们最终都到达了同一个位置，那么n当然是（wx,0,0）（0,wy,0）（0,0,wz）三个向量的矢量和啦！

在这里我们一定要认清，向量是与坐标系没有关系的！向量就是向量，是固定的！它只是在不同的坐标系表示的坐标不同罢了！

我们被很多书上的图误导了

就像这样的图，先入为主的认为n是在地理坐标系的，然后去想飞机是怎么旋转的，怎么想也想不明白！当我们谈到向量，我们一定要认为他是独立的存在空间的，跟坐标系什么关系都没有！

四元数的本质就是，飞机可以看成绕三个向量x,y,z三步旋转到最终位置，也可以看成绕一个向量n一步旋转到最终位置。那么当然n=x+y+z啦，这里是矢量和。

我们始终要牢记：向量是独立的！跟坐标系没有任何关系！

n、θ和欧拉角的关系，我一直讲的是角速度，其实应该是角度的增量。θ应该是三个角度增量的长度。下面是PX4的代码。

// Convert the rotation vector to its equivalent quaternion
rotationMag = correctedDelAng.length();
if (rotationMag < 1e-12f)
{
deltaQuat[0] = 1.0;
deltaQuat[1] = 0.0;
deltaQuat[2] = 0.0;
deltaQuat[3] = 0.0;
}
else
{
// We are using double here as we are unsure how small
// the angle differences are and if we get into numeric
// issues with float. The runtime impact is not measurable
// for these quantities.
deltaQuat[0] = cos(0.5*(double)rotationMag);
float rotScaler = (sin(0.5*(double)rotationMag))/(double)rotationMag;
deltaQuat[1] = correctedDelAng.x*rotScaler;
deltaQuat[2] = correctedDelAng.y*rotScaler;
deltaQuat[3] = correctedDelAng.z*rotScaler;
}

// Update the quaternions by rotating from the previous attitude through
// the delta angle rotation quaternion
qUpdated[0] = states[0]*deltaQuat[0] - states[1]*deltaQuat[1] - states[2]*deltaQuat[2] - states[3]*deltaQuat[3];
qUpdated[1] = states[0]*deltaQuat[1] + states[1]*deltaQuat[0] + states[2]*deltaQuat[3] - states[3]*deltaQuat[2];
qUpdated[2] = states[0]*deltaQuat[2] + states[2]*deltaQuat[0] + states[3]*deltaQuat[1] - states[1]*deltaQuat[3];
qUpdated[3] = states[0]*deltaQuat[3] + states[3]*deltaQuat[0] + states[1]*deltaQuat[2] - states[2]*deltaQuat[1];

// Normalise the quaternions and update the quaternion states
quatMag = sqrtf(sq(qUpdated[0]) + sq(qUpdated[1]) + sq(qUpdated[2]) + sq(qUpdated[3]));
if (quatMag > 1e-16f)
{
float quatMagInv = 1.0f/quatMag;
states[0] = quatMagInv*qUpdated[0];
states[1] = quatMagInv*qUpdated[1];
states[2] = quatMagInv*qUpdated[2];
states[3] = quatMagInv*qUpdated[3];
}

correctedDelAng是实时测量的角速度乘以采样周期T。

这里Q的更新采用的是Q=QXΔQ。依据如下：

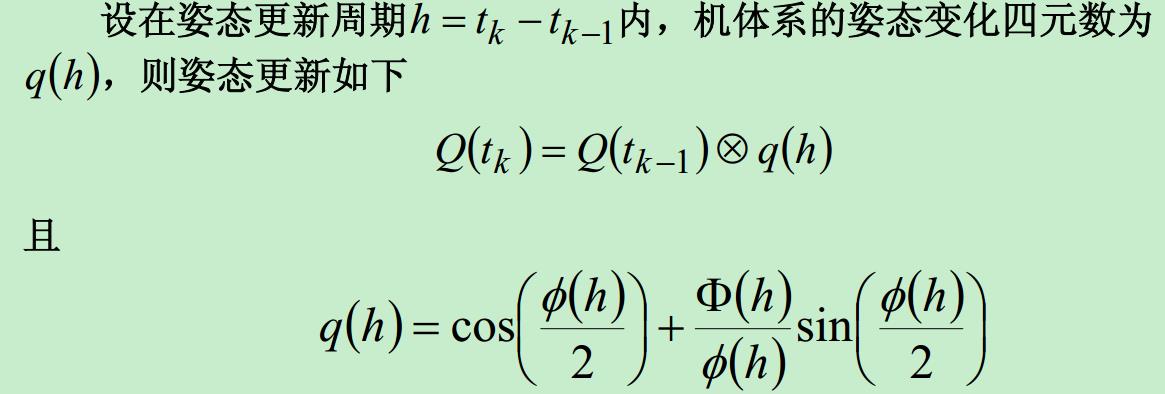
 即两个四元数相乘，表示两次旋转。初始的旋转加上此次的旋转增量，即为此刻的旋转矩阵了。

5.今天又看到另外一种求四元数与姿态角的关系的。感觉这种方法更直观。

把姿态角的三次旋转就看成三次四元数旋转，然后q1q2q3就是四元数最终旋转矩阵了。

cosRoll = cosf(initialRoll * 0.5f);
sinRoll = sinf(initialRoll * 0.5f);

cosPitch = cosf(initialPitch * 0.5f);
sinPitch = sinf(initialPitch * 0.5f);

cosHeading = cosf(initialHdg * 0.5f);
sinHeading = sinf(initialHdg * 0.5f);

initQuat[0] = cosRoll * cosPitch * cosHeading + sinRoll * sinPitch * sinHeading;
initQuat[1] = sinRoll * cosPitch * cosHeading - cosRoll * sinPitch * sinHeading;
initQuat[2] = cosRoll * sinPitch * cosHeading + sinRoll * cosPitch * sinHeading;
initQuat[3] = cosRoll * cosPitch * sinHeading - sinRoll * sinPitch * cosHeading;

这是PX4给Q赋初值的代码，就是采用的5这种方法。按理来说这才是最合理的。一开始就把三次旋转就用四元数表示了。至于上面的那种办法，合并旋转轴，也是对的。