20161111双十一特价模拟赛
Posted Konjak谷弱
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了20161111双十一特价模拟赛相关的知识,希望对你有一定的参考价值。
Ib的沙漏(hourglass)
正当Ib欣赏着一副诡异的画时,大厅的灯闪烁了几下,便熄灭了
墙上流出了蓝色的液体,上面写着……
Ib满怀着恐惧的走出大厅,发现整个美术馆已经空无一人,大门紧锁,灯光也暗淡了下来,正当她感到无望时,她想起了自己的神奇沙漏,这个沙漏由n个小沙漏组成,第i个小沙漏的沙子数量为ai,这个沙漏有一个神奇的性质,如果用手拨动第i个小沙漏,这个沙漏的沙子数量会变成sqrt(ai)(向下取整),Ib经常玩弄她的沙漏以打发时间,有时她会用手连续拨动第l到r个小沙漏,有时她会数第l到r个小沙漏的沙子数量之和为多少,可惜Ib今早把沙漏忘在家里了,希望你能帮她模拟一个沙漏,这样也许她就不会害怕了,额…
Input
第一行一个整数n
第二行n个整数a1,a2,…,an,(0<=ai<=10^9)
第三行一个整数m表示Ib玩弄沙漏的次数
接下来m行,每行三个整数t,l,r
若t=1表示Ib数第l到r个小沙漏的沙子数量之和
若t=2表示Ib拨动第l到r个小沙漏
Output
每次t=1时,每行一个整数,表示第l到r个小沙漏的沙子数量之和
Sample Input
4
1 100 5 5
5
1 1 2
2 1 2
1 1 2
2 2 3
1 1 4
Sample Output
101
11
11
数据范围:
30%:n,m<=1000
100%:n,m<=100000
我们可以发现一个10^9的数最多开方5次就变成1了。
然后在线段树上维护一个标记(当前是否全是0或者1)。
修改最多就5nlogn

1 #include<cstdio>
2 #include<cstdlib>
3 #include<cstring>
4 #include<cmath>
5 #include<algorithm>
6 #include<iostream>
7 using namespace std;
8
9 typedef long long LL;
10 const int N=2*100010;
11 int n,m,tl;
12 LL a[N];
13 struct trnode{
14 int l,r,lc,rc,c;
15 LL sum;
16 }t[2*N];
17 int o=0;
18
19 int bt(int l,int r)
20 {
21 int x=++tl;
22 t[x].l=l;t[x].r=r;
23 t[x].lc=t[x].rc=0;
24 t[x].c=0;t[x].sum=0;
25 if(l<r)
26 {
27 int mid=(l+r)/2;
28 t[x].lc=bt(l,mid);
29 t[x].rc=bt(mid+1,r);
30 int lc=t[x].lc,rc=t[x].rc;
31 t[x].c=t[lc].c&t[rc].c;
32 t[x].sum=t[lc].sum+t[rc].sum;
33 }
34 else
35 {
36 if(a[l]==1 || a[l]==0) t[x].c=1;
37 t[x].sum=a[l];
38 }
39 return x;
40 }
41
42 LL query(int x,int l,int r)
43 {
44 if(t[x].l==l && t[x].r==r) return t[x].sum;
45 int lc=t[x].lc,rc=t[x].rc,mid=(t[x].l+t[x].r)/2;
46 if(r<=mid) return query(lc,l,r);
47 if(l>mid) return query(rc,l,r);
48 return query(lc,l,mid)+query(rc,mid+1,r);
49 }
50
51 void change(int x,int l,int r)
52 {
53 if(t[x].l==l && t[x].r==r && t[x].c==1) return ;
54 if(t[x].l==t[x].r)
55 {
56 t[x].sum=(LL)sqrt((double)t[x].sum);
57 if(t[x].sum==1 || t[x].sum==0) t[x].c=1;
58 // if(o) printf("t[x] .l = %d r = %d c = %d sum = %d\\n",t[x].l,t[x].r,t[x].c,t[x].sum);
59 return;
60 }
61 int lc=t[x].lc,rc=t[x].rc,mid=(t[x].l+t[x].r)/2;
62 if(r<=mid) change(lc,l,r);
63 else if(l>mid) change(rc,l,r);
64 else
65 {
66 change(lc,l,mid);
67 change(rc,mid+1,r);
68 }
69 t[x].c=t[lc].c&t[rc].c;
70 t[x].sum=t[lc].sum+t[rc].sum;
71 // if(o) printf("t[x] .l = %d r = %d c = %d sum = %d\\n",t[x].l,t[x].r,t[x].c,t[x].sum);
72 }
73
74 int main()
75 {
76 // freopen("a.in","r",stdin);
77 // freopen("a.out","w",stdout);
78 freopen("hourglass.in","r",stdin);
79 freopen("hourglass.out","w",stdout);
80 scanf("%d",&n);
81 for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
82 tl=0;t[0].sum=0;t[0].c=1;
83 bt(1,n);
84 scanf("%d",&m);
85 int tmp,l,r;
86 for(int i=1;i<=m;i++)
87 {
88 scanf("%d%d%d",&tmp,&l,&r);
89 if(l>r) swap(l,r);
90 if(tmp==1) printf("%lld\\n",query(1,l,r));
91 else change(1,l,r);
92 }
93 return 0;
94 }
诡异的雕塑(sculpture)
玩腻了沙漏的Ib决定勇敢地前进,她走进了一幅画中,来到了画中的世界!额… 在这里她遇到了与自己一样迷失在画中的Garry,
于是他们决定结伴而行,继续在画中的世界探索。
他们来到了一个绿色房间,这个房间没有出口,只有一排诡异的雕塑,聪明的Ib一看就知道要怎么做了,这里一共有n个雕塑,第i个雕塑的高度位hi,只要把这些雕塑摆成类似于一个山峰的形状就行了,具体地说,存在i使得对于1<=j<i,h[j]<=h[j+1], 对于i<j<=n,h[j-1]>=h[j],摆成这样后,房间的,们就会自动打开,当然Ib可搬不动这些雕塑,她只能向Garry求助,Garry每次只能交换相邻的两个雕塑,为了帮Garry节省力气继续后面的闯关,请你求出最少的交换次数。
Input
第一行一个正整数n
接下来n行,第i行一个整数hi
Output
输出一个整数,表示Garry最少需要的交换次数
Sample Input
6
2
8
4
5
3
6
Sample Output
3
HINT
最终的高度序列为2 4 5 8 6 3,共需要操作三次。
3<=n<=3*10^5
1<=hi<=10^9
数据范围
30% n<=10
100% n<=300000
这题没做出来是真的不应该。。这不就是之前的逆序空位插入法吗?!
首先我们给原序列一个编号1,2,3,...,n
假设按最后的状态是2,3,5,...,1
每个元素的交换次数就是逆序对的个数。
当然我们可以不这样想。
对于每个元素,从小到大先排序,我们考虑当前最小的。
它一定会走到最左或者最右边,而且它到了之后对后边的答案没有影响(它到了之后没有东西会来跟它交换位置)
模拟样例吧:
2 8 4 5 3 6
编号 1 2 3 4 5 6
对于2,它到最左边不需要交换。ans+0;
变成 8 4 5 3 6
编号 2 3 4 5 6
对于3,它到最左边要3次,到最右边1次。ans+1
变成 8 4 5 6
编号 2 3 4 6
.............
以此类推,每次删除一个数之后都要在树状数组上删除它。
注意相等的数之间是不会产生逆序对的(不然你就直接当它们交换了位置)
1 #include<cstdio>
2 #include<cstdlib>
3 #include<cstring>
4 #include<iostream>
5 #include<cmath>
6 #include<algorithm>
7 using namespace std;
8
9 typedef long long LL;
10 const int N=300010;
11 int n,c[N];
12 struct node{int d,id;}a[N];
13
14 bool cmp(node x,node y){return x.d<y.d;}
15 int minn(int x,int y){return x<y ? x:y;}
16
17 int add(int x,int d)
18 {
19 for(int i=x;i<=n;i+=(i&(-i))) c[i]+=d;
20 }
21 int getsum(int x)
22 {
23 int ans=0;
24 for(int i=x;i>=1;i-=(i&(-i))) ans+=c[i];
25 return ans;
26 }
27
28 int main()
29 {
30 // freopen("a.in","r",stdin);
31 // freopen("a.out","w",stdout);
32 freopen("sculpture.in","r",stdin);
33 freopen("sculpture.out","w",stdout);
34 scanf("%d",&n);
35 for(int i=1;i<=n;i++)
36 {
37 scanf("%d",&a[i].d);
38 a[i].id=i;
39 }
40 sort(a+1,a+1+n,cmp);
41 memset(c,0,sizeof(c));
42 for(int i=1;i<=n;i++) add(i,1);
43 int k=1,s=n,now;
44 LL ans=0;
45 for(int i=1;i<=n+1;i++)
46 {
47 if(a[i].d==a[i-1].d) continue;
48 for(int j=k;j<i;j++) add(a[j].id,-1),s--;
49 for(int j=k;j<i;j++)
50 {
51 now=getsum(a[j].id-1);
52 ans+=(LL)minn(now,s-now);
53 }
54 k=i;
55 }
56 printf("%lld\\n",ans);
57 return 0;
58 }
Mary的游戏(game)
继续前进Ib和Garry又遇见了迷失在画中的世界里的Mary(左)
现在Mary被一个游戏难住了,没有玩出这个游戏Mary就不走了,可是以Mary的智商恐怕很难通关,为了尽快逃离这个地方,请你这帮Mary通关吧
Mary有一个n*m的矩形卡片,每个格子有权值Aij,每条边有权值,现在Mary要求一个联通块,使得格子的权值Aij/联通块边界上的边的权值之和最大。具体见样例
Input
第一行为两个正整数n,m。
接下来n行,每行m个非负整数,表示对应格子的价值。
接下来n+1行,每行m个正整数,表示所有横向的格线上的费用。
接下来n行,每行m+1个正整数,表示所有纵向的格线上的费用。
(所有数据均按从左到右,从上到下的顺序输入,参见样例和配图)
Output
输出一行仅含一个数,表示最大的V/C,保留3位小数。
Sample Input
3 4
1 3 3 3
1 3 1 1
3 3 1 0
100 1 1 1
97 96 1 1
1 93 92 92
1 1 90 90
98 1 99 99 1
95 1 1 1 94
1 91 1 1 89
Sample Output
1.286
HINT
数据范围 30% n,m<=5 100% n,m<=50
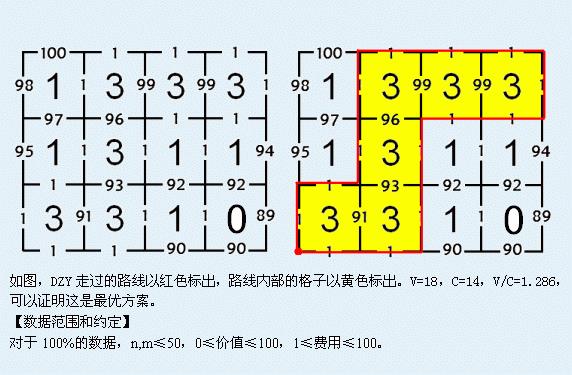
这题明显01分数规划,r=v/c;
设z=v-rc,我们二分r,然后判断z是否可以>=0。
然后我们发现最小割上不跑z就可以==0,那就一个连通块都没有。。那么我们判断的时候直接让z>0才可以。
之前一直在纠结一个联通块的问题,但是其实要是有两个连通块让z>0那也是没有关系的,因为我们已经转化成判定性问题,那这两个之中必定有1个能让z>0。
那就转化成了一个经典的网络流问题,也就是之前的海洋陆地问题。
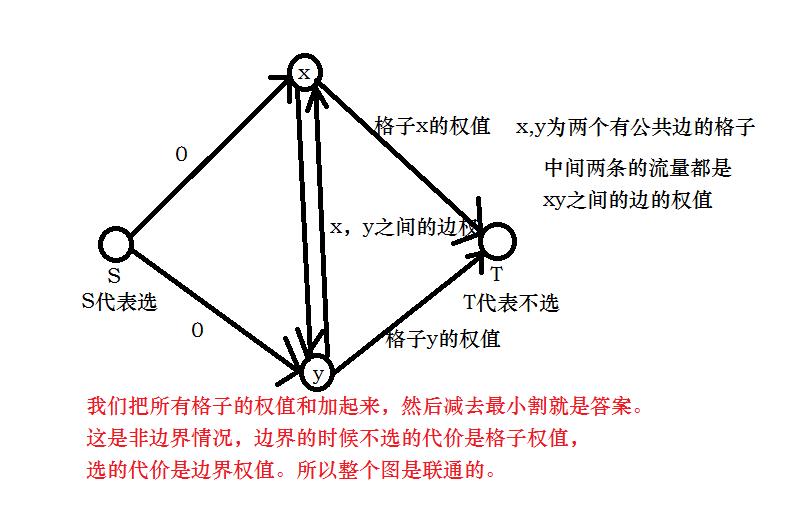
1 #include<cstdio>
2 #include<cstdlib>
3 #include<cstring>
4 #include<cmath>
5 #include<algorithm>
6 #include<iostream>
7 #include<queue>
8 using namespace std;
9
10 const int N=3010;
11 const double INF=(double)1e9;
12 int n,m,len,dis[N],first[N];
13 int dx[3]={0,-1,0};
14 int dy[3]={0,0,-1};
15 double sum,A[60][60],b[60][60],c[60][60];
16 struct node{
17 int x,y,next;
18 double d;
19 }a[100010];
20 queue<int> q;
21
22 int idx(int x,int y){return (x-1)*m+y;}
23 double myabs(double x){return x>0 ? x:-x;}
24 double minn(double x,double y){return x<y ? x:y;}
25
26 void ins(int x,int y,double d)
27 {
28 a[++len].x=x;a[len].y=y;a[len].d=d;
29 a[len].next=first[x];first[x]=len;
30
31 a[++len].x=y;a[len].y=x;a[len].d=0;
32 a[len].next=first[y];first[y]=len;
33 }
34
35 bool bfs(int st,int ed)
36 {
37 while(!q.empty()) q.pop();
38 memset(dis,-1,sizeof(dis));
39 q.push(st);dis[st]=0;
40 while(!q.empty())
41 {
42 int x=q.front();q.pop();
43 for(int i=first[x];i!=-1;i=a[i].next) if(a[i].d>0)
44 {
45 int y=a[i].y;
46 if(dis[y]==-1)
47 {
48 dis[y]=dis[x]+1;
49 q.push(y);
50 }
51 }
52 }
53 return (dis[ed]!=-1);
54 }
55
56 double dfs(int x,int ed,double flow)
57 {
58 if(x==ed) return flow;
59 double r=0,p;
60 for(int i=first[x];i!=-1;i=a[i].next) if(a[i].d>0)
61 {
62 int y=a[i].y;
63 if(dis[y]==dis[x]+1)
64 {
65 p=minn(flow-r,a[i].d);
66 p=dfs(y,ed,p);
67 r+=p;
68 a[i].d-=p;
69 a[i^1].d+=p;
70 }
71 if(myabs(r-flow)<0.00001) break;
72 }
73 if(r==0) dis[x]=-1;
74 return r;
75 }
76
77 double dinic(int st,int ed)
78 {
79 double ans=0;
80 while(bfs(st,ed)) ans+=dfs(st,ed,INF);
81 // printf("ans = %lf\\n",ans);
82 return ans;
83 }
84
85 void output()
86 {
87 for(int i=0;i<=len;i+=2)
88 {
89 printf("%d -- > %d %lf\\n",a[i].x,a[i].y,a[i].d);
90 }
91 }
92
93 bool check(double r)
94 {
95 len=-1;
96 memset(first,-1,sizeof(first));
97 int S=0,T=n*m+1,x,y;
98 double w;
99 for(int i=1;i<=n;i++)
100 for(int j=1;j<=m;j++)
101 {
102 w=0;
103 if(i==1 || j==1 || i==n || j==m)
104 {
105 if(i==1) w+=r*b[i][j];
106 if(j==1) w+=r*c[i][j];
107 if(i==n) w+=r*b[i+1][j];
108 if(j==m) w+=r*c[i][j+1];
109 }
110 ins(S,idx(i,j),A[i][j]);
111 if(w) ins(idx(i,j),T,w);
112 for(int k=1;k<=2;k++)
113 {
114 x=i+dx[k];y=j+dy[k];
115 if(x<1 || y<1) continue;
116 w=(k==1) ? r*b[i][j] : r*c[i][j];
117 ins(idx(i,j),idx(x,y),w);
118 ins(idx(x,y),idx(i,j),w);
119 以上是关于20161111双十一特价模拟赛的主要内容,如果未能解决你的问题,请参考以下文章
2021年大数据Flink(四十):Flink模拟双十一实时大屏统计
年年双十一,年年抢不到,自制Python淘宝秒杀抢购脚本,百分百中
