回溯法解决八皇问题

Posted 2020-06-14

把八个皇后放在一个8*8的棋盘上面，要求同一行、同一列、同一对角线不能有两个皇后。

思路：
关键在于判定两个皇后是否在同一行、同一列或同一
对角线上。这里，棋盘下标从1开始算起。
观察发现：
若是在同一行，则行号相同；
若在同一列，则列号相同；
若在同一“/”对角线，则行列值之和相同；
若是在同一“\”对角线，则行列值之差相同。
考虑到每行仅有一个皇后，设一维数组a[1...8]表示皇后的位置：
第i行第j列放置皇后，则a[i]=j，即下标是行数，值是列数。
判断皇后是否安全，即检查同一列、同一对角线是否已经有皇后。
建立标志数组b[1...8]能控制同一列只能有一个皇后。若两个皇后
在同一对角线上，则其行列值之和或差相等，故亦可以建立标志数组
c[1...16],d[-7..7]控制同一对角线上只能有一个皇后。（注意：
这里的c和d数组是对应主、副各自16条对角线的.）
若是斜线不分方向，则同一斜线上两个皇后的行号之差的绝对值与列号
之差的绝对值相等。在这种方式下，要表示两个皇后i和j不在
同一列或斜线上的条件可以描述为：(a[i]!=a[j])&&(abs（a[i]-a[j]）)
i和j分别表示两个皇后的行号。

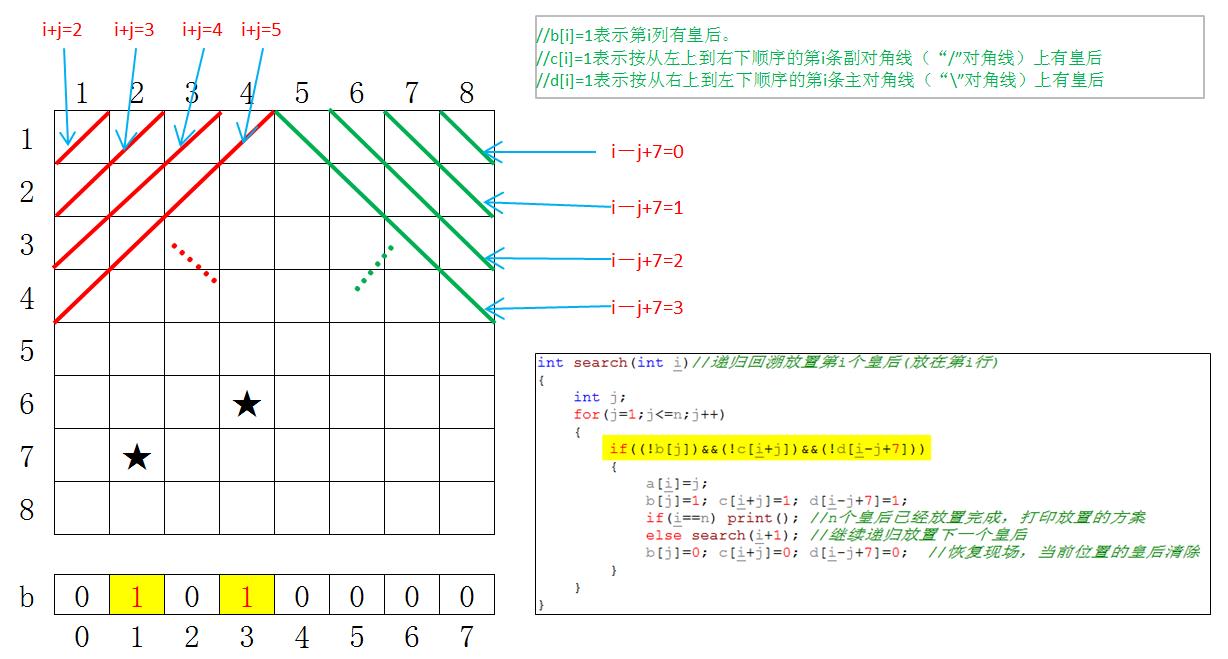
具体代码如下：

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 int n;
 4 int sum=0,a[100];//sum表示总的方案数。a[i]=x表示第i行放在x列
 5 int b[100]={0},c[100]={0},d[100]={0};
 6 //b[i]=1表示第i列有皇后。
 7 //c[i]=1表示按从左上到右下顺序的第i条副对角线（“/”对角线）上有皇后
 8 //d[i]=1表示按从右上到左下顺序的第i条主对角线（“\”对角线）上有皇后
 9 int search(int i);//递归回溯放置第i个皇后(放在第i行)
10 void print();      //输出方案
11 int main()
12 {
13     n=8;//皇后问题的阶数（皇后的个数）
14     search(1);
15     if(sum==0) printf("no solution！\n");
16     return 0;
17 }
18 int search(int i)//递归回溯放置第i个皇后(放在第i行)
19 {
20     int j;
21     for(j=1;j<=n;j++)
22     {
23         if((!b[j])&&(!c[i+j])&&(!d[i-j+7]))
24         {
25             a[i]=j;
26             b[j]=1; c[i+j]=1; d[i-j+7]=1;
27             if(i==n) print(); //n个皇后已经放置完成，打印放置的方案
28             else search(i+1); //继续递归放置下一个皇后
29             b[j]=0; c[i+j]=0; d[i-j+7]=0;  //恢复现场，当前位置的皇后清除
30         }
31     }
32 }
33 void print()
34 {
35     int i;
36     sum++;
37     printf("sum=%d\n",sum);
38     for(i=1;i<=n;i++)
39         printf("%-4d ",a[i]);
40     printf("\n");
41 }

PS：个人觉得该段代码里面标志数组b、c、d用的非常巧妙。

上面的代码是多用了两个数组c、d简化了判断。假如只用一个数组b也能够判断皇后会否冲突，只是时间效率降低了很多。代码如下：

 1 #include <stdio.h>
 2 int n;
 3 int sum=0,a[100]; //sum表示总的方案数。a[i]=x表示第i行放在x列
 4 int b[100]={0};   //b[i]=1表示第i列有皇后。
 5 
 6 int search(int i);//递归回溯放置第i个皇后(放在第i行)
 7 void print();      //输出方案
 8 int main()
 9 {
10     n=8;//皇后问题的阶数（皇后的个数）
11     search(1);
12     if(sum==0) printf("no solution！\n");
13     return 0;
14 }
15 int search(int i)//递归回溯放置第i个皇后(放在第i行)
16 {
17     int j,k;
18     for(j=1;j<=n;j++)
19     {
20         if(b[j]==0)
21         {
22             for(k=1;k<i;k++)//扫描a[]前i-1项，检查前i-1个皇后会否与第i个皇后冲突 
23             {
24                 if(k+a[k]==i+j) break;
25                 else if(k-a[k]==i-j) break;
26             }
27             if(k==i)//前i-1个皇后不与第i个皇后冲突
28             {
29                 a[i]=j;
30                 b[j]=1;
31                 if(i==n) print(); //n个皇后已经放置完成，打印放置的方案
32                 else search(i+1); //继续递归放置下一个皇后
33                 b[j]=0; //恢复现场，当前位置的皇后清除
34             }
35         }
36     }
37 }
38 void print()
39 {
40     int i;
41     sum++;
42     printf("sum=%d\n",sum);
43     for(i=1;i<=n;i++)
44         printf("%-4d ",a[i]);
45     printf("\n");
46 }

View Code