机器学习笔记—svm算法（上）

Posted 2020-08-13 小花花108

本文申明：本文原创，如转载请注明原文出处。

引言：上一篇我们讲到了logistic回归，今天我们来说一说与其很相似的svm算法，当然问题的讨论还是在线性可分的基础下讨论的。

很多人说svm是目前最好的分类器，那我们就来看看我们的svm好在哪里。

一：初识svm

问题：用一条直线把下图的圆球和五角星分离开来。

解答：有N种分法，如下图：

附加题：找出最佳分类？

解答：如图：

Exe me?鬼知道哪一条是最佳？？

等等这个最佳分类是不是等价于，地主让管家给两个儿子分地，是不是只要让两家之间一样多就可以了？那是不是就是那根红线让两家距离之和离分界线最远就可以了？

恭喜你，猜对了。

现在我们把问题上升到N维，就是说，我也不知道这个N维是什么样子，但是，我要在N维中把这两个东东分离开来。那么从直线ax+b就可以表示成超平面W^Tx+b去分开。示意图如下：

其中W=(W₁;W₂;…;W_d)为法向量，决定了这个超平面的方向，b为位移项，决定了超平面与原点之间的距离。显然这个超平面就是被W和b确定的。那求出这个超平面这个分类模型不就建立了吗。那就是最优化求最大间隔的问题。

说到间隔（margin）问题，我们来科普下函数间隔和几何间隔。

1.1函数间隔（functional margin）

假设图中A,B,C表示三个实例，A离超平面最近，那么预测正确的可能性就比较低，但是C离超平面H最远，那么预测正确的概率就比较高，B介于两者之间。

一般来说，一个点到一个超平面的距离可以表示为这个点预测的确信程度。这就是函数间隔。

对于给定的训练数据集T和超平面(w,b)，定义超平面关于样本点(x_i,y_i)的函数间隔为：

1.2 几何间隔

函数间隔可以表示预测的正确性以及确信度，但是当我们选择最优的超平面的时候，只有函数间隔还不够，主要按照比例改变W和b那么超平面没有变，但是函数间隔却变成了原来的两倍，我们可以对分离超平面的法向量进行约束，例如规范化，||w||=1,这样就使得间隔是确定的，这样函数间隔就变成了几何间隔。

假设B在这条分割线面上，分割线外的一点，到这个平面的距离用表示，任何一个点在这个超平面分割面上都有一个投影，现在假设，A的投影就是B，那么BA就是A到B的距离，w就是它的法向量,其中w/||w||为单位向量，假设A（xⁱ,yⁱ）那么B的x坐标为xⁱ- w/||w||。把B的横坐标带入wTX+b=0,得到：

进一步化简：

所以当||w||=1的时候，无乱扩大几倍，对距离都没有影响，这叫做几何距离。

1.3间隔最大化

现在我们知道分离超平面有无数个，但是几何间隔最大化只有一个，而SVM的思想就是寻找这个能让间隔最大化的超平面，把这个作为分类的标准。那么这个问题就可以表示成约束最优化问题：

s.t.

       ||w||=1

这里用||w||=1 规约 w，使得 + 是几何间隔,考虑到函数间隔和几何间隔的关系：

所以上述公式可以改写为：

s.t.

求上述的最大值，就等价于求||w||的最小值问题。等价于：

Min (w,b)

s.t.

好了终于到这一步了。

接下来介绍的是手工求解的方法了，一种更优的求解方法。

二：学习的对偶算法

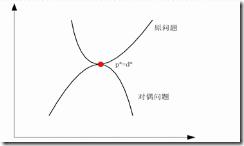
为了求解线性可分的支持向量机的最优化问题，将它作为原始最优化问题，应用拉格朗日对偶性，求解对偶性问题去得到原始问题，这就是线性可分支持向量机的对偶算法。思想如图所示：

我想大家一看就会明白了。。。

补充（来自维基百科）：

首先，我们定义拉格朗日函数，对每一个不等式的约束条件引进拉格朗日乘子aⁱ>=0,i=1,2,3..,N,.则函数1为：

。

根据拉格朗日对偶性，原始问题的对偶问题是极大极小值问题：

那么为了得到对偶问题的解，需要先求L(w,b,a)的极小，再求对a的极大。

2.1求min L(w,b,a)

首先对函数1 分别对w,b求偏导并令其为0.

那么：

将上述两式带入到函数1可得：

即：

2.2求min L(w,b,a)对a的极大，即使对偶问题

。

这样就可以得到与之等价的对偶最优化问题：

。

现在对上式中a的解为a^*=( a₁^*, a₂^*,…a_n^*)^T,因为满足KKT条件那么就可以求得最优化问题的解w^*,b^*.

综上，分类决策函数可以写成：

下期预告：下期将会为大家带来线性不可分的情况，也是SVM最核心的“核武器”以及svm的优缺点，敬请关注！