线性代数和numpy

Posted 2020-08-12 段子手实习生

一、代数是什么

　　代数->数的抽象表示->向量空间（线性空间）

　　线代->线性代数

 

关系：

　　向量空间之间和内部转换是通过线性变换。

实数——一维空间的点

复数——二维空间的点

　　如果两个向量的组合可以生成平面，则要求两个向量要线性无关。

　　推广一下，N维空间里点可以用N个线性无关的向量来表示。这N个向量就是这个平面的基。

　　向量的封闭——对加法和数乘封闭。

　　　　向量V中任意两个向量a,b加法a+b，仍然在V中，实数乘法x*b,仍然也在V中。

 

线性相关——其中的一个向量可以用其他的向量表示出来。

 

矩阵操作在python里编程依赖一个最常用的库——numpy

 

1、矩阵的创建

a=np.arange(1,5)
a=np.array([1,2,3,4,5])
print a, a.dtype, a.shape, a.size, a.ndim

np.arange类似range函数
np.array用来生成矩阵
dtype是数据类型，有int64, complex, uint16等
shape是个元组属性，表示每一维的宽度
size是所有元素个数
ndim是维数

b=np.array([1,2,3],dtype=\'float16\') # int64, complex, uint16......
print b, b.dtype

 

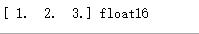
m=np.array([np.arange(6),np.arange(6)])
print m, m.shape, m.size

# 每一个[]代表一维，比如
# [[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]], 代表矩阵的维度是(2,2,3)
# 其中第一个2，代表最外层的两个[]，第二个2代表第二层[]，第三个3代表最里层的维度。
n=np.array([[1,2,3,4],[5,6,7,8]])
print n, n[0,2], n[1,1]

m=np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
print m.shape

 

x=m.ravel()
y=n.flatten()
print x
print y

 

 

 

ravel()和flatten()看起来效果一样，都是把矩阵展平了。它们的区别在于
ravel()返回的是原有数据的一个映射(view)，没有分配新的存储
flatten()返回的是新的数据
因此如果我们改变它们的值，就可以看出区别

numpy还有一些函数有这样的区别，关键在于判断函数返回是原数据的映射还是返回新的数据。

…… 

等等一共三十道题，详情可参阅黑板课老师的notebook。

 

 

正交：A矩阵的转置乘以B等于0。

可逆：方阵，行数等于列数

　　　列向量线性无关

 

 

最小二乘法——投影解释

　　　　二维平面上，一个点向一条直线投影。

　　　　扩展到N维里边，就是让一个直线拟合若干个点，让这些点到线的距离和最短。y=ax+b

　　　　但有的时候，欠拟合，可以往更高维的空间投影，y=ax^3+bx^2+cx+d，或者更高维的空间。

　　　　但维数过高容易过拟合。

 

行列式

　　从平行四边形的面积推出来。

 

 

 

 

特征值和特征向量

　　AX=λX——向量X经过向量A的线性变换，得到的是向量A的倍数。λ称为A的特征值，X称为A的特征向量。

　　什么意思呢？X经过A的变换，得到的是X的方向的伸缩。

　　在matlab里边有例子，eigshow，然后运行，推重两个向量重合时，重合的向量就是特征向量。两个向量成一条直线的时候，也会有特征向量。然后反方向，所以有四组。从图形中看，是一个椭圆和圆的交合。

　　如何求特征值和特征向量？

 

 

 

如何用特征值和特征向量来求Fibonacci序列