四边形不等式HDU3516-Tree Construction

Posted 2020-08-10 Yiyi

【题目大意】

给定n个点(x,y)，并且保证xi<xj&&yi>yj当i<j。要求建一颗树，树的边只能向上和向右生长，求将所有点都连起来树的长度最小。

【思路】

定义状态 dp[i,j]表示点i到点j合并在一起的最小花费（树枝的长度）。如dp[3,4]表示图中绿色的这一段。

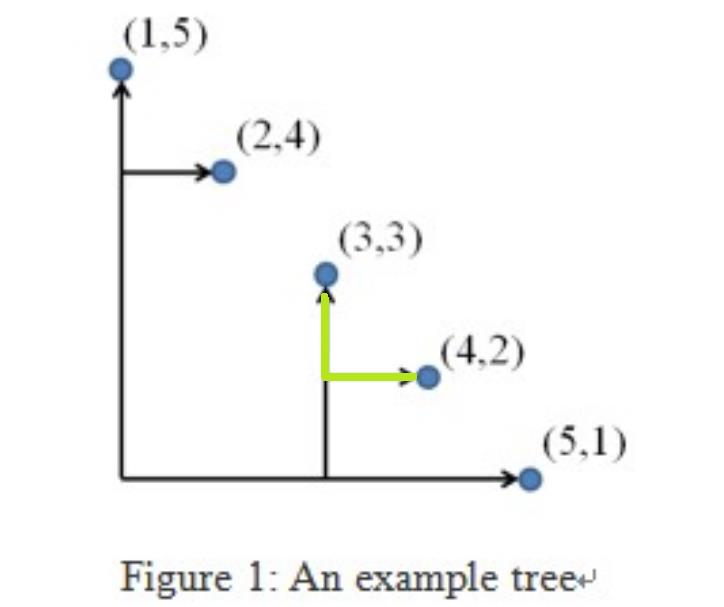
状态转移方程：dp[i,j]= min(dp[i,k]+dp[k+1,j]+w(i,j) ) i<k<j，w(i,j)=py[k]-py[j]+px[k+1]-px[i]。

【注意点】

初始化的时候s[i][i]=i-1，因为i<k<j，k不能取i。

 

 1 #include<cstdio>  
 2 #include<cstring>  
 3 #include<iostream>  
 4 #include<algorithm>  
 5 using namespace std;  
 6 const int MAXN=1010;
 7 const int INF=1e9;
 8 //这里INF设太大会溢出来 
 9 int T,t,n;  
10 int dp[MAXN][MAXN],s[MAXN][MAXN];
11 int x[MAXN],y[MAXN];  
12 
13 void solve()
14 {
15     for(int i=n;i>=1;i--)  
16         for(int j=i+1;j<=n;j++)  
17         {  
18             dp[i][j]=INF;  
19             for(int k=s[i][j-1];k<=s[i+1][j];k++)  
20             {  
21                   int ret=dp[i][k]+dp[k+1][j]+x[k+1]-x[i]+y[k]-y[j];  
22                    if(ret<dp[i][j])  
23                    {  
24                     dp[i][j]=ret;  
25                     s[i][j]=k;  
26                 }  
27             }  
28         }  
29     printf("%d\\n",dp[1][n]);  
30 }
31 
32 void init()
33 {
34     for(int i=1;i<=n;i++)  
35         scanf("%d%d",&x[i],&y[i]); 
36     memset(dp,0,sizeof(dp));
37     memset(s,0,sizeof(s)); 
38     for(int i=1;i<=n;i++)  
39         s[i][i]=i-1;  
40 }
41 
42 int main()  
43 {   
44     while(~scanf("%d",&n))  
45     {  
46         init();
47         solve();
48     }  
49 }