结题报告——2018级2016第二学期第三周作业9.24

Posted 2020-08-10

题目一:〖NOIP2002P〗过河卒

描述

　　如图，A 点有一个过河卒，需要走到目标 B   点。卒行走规则：可以向下、或者向右。同时在棋盘上的任一点有一个对方的马（如上图的C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例 如上图 C  点上的马可以控制 9 个点（图中的P1，P2 … P8 和 C）。卒不能通过对方马的控制点。 

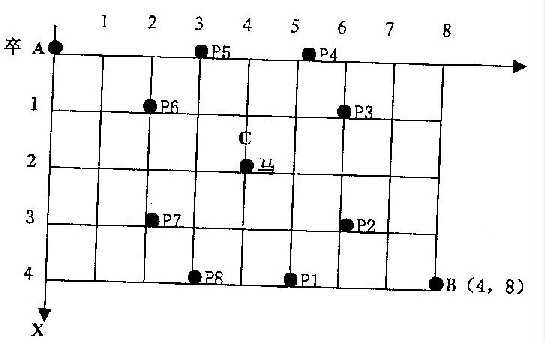
棋盘用坐标表示，A 点（0，0）、B 点（n,m）(n,m 为不超过 20  的整数，并由键盘输入)，同样马的位置坐标是需要给出的（约定: C<>A，同时C<>B）。现在要求你计算出卒从 A 点能够到达 B  点的路径的条数。

输入　　　

B点的坐标（n,m）以及对方马的坐标（X,Y）{不用盘错}

输出　　　　

一个整数（路径的条数）。

样例输入

6 6 3 2

样例输出

17

分析：

我们都知道，在没有“马”的情况下，求从A点到达B点（x,y）路径的条数可以用递归式来表达；

即分为两种情况：

1.在边缘部分

当x=0时，到达这个点的路径只能是从上面一个点过来的（除原点外），即为f(x,y)=f(x，y-1) (x=0)

当y=0时，则恰好相反，到达这个点的路径只能是从左面一个点过来的（除原点外），即为f(x,y)=f(x-1，y) (y=0)

2.在中间部分

因为题目规定“可以向下、或者向右”，所以在中间部分的点只能是来自上方，或下方，

所以到这个点的路径数等于到达上方点的路径数加上到达左方点的路径数，即为f(x,y)=f(x-1,y)+f(x,y-1);

 

but 在图中有一“马”（a,b)的情况下，(a,b),(a-1,b-2),(a-1,b+2),(a+1,b-2),(a+1,b+2)等点无法通行，

即为路径数为0，但是这样太过繁琐，所以我们经过观察，可以发现，(x==a&&y==b)或者(abs(a-x)*abs(b-y)==2）

两种情况下都无法通行，至于第二种情况则是因为a-x与b-y两者之间一者为正负1，一者为正负2；

 

就这样，我们得到了这样一组递归式，但是我用回溯和递归分别做出来之后，却超时了；

于是，我认为应使用递归的思想实行递推，就建立了qipan数组，储存从左上角到任意一点的路径数，最后输出qipan(x,y），最终AC；

过程如下，自不必多说：

for(int i=0;i<=n;i++)
    for(int j=0;j<=m;j++)
    {
        if(i==0&&j==0)qipan[i][j]=1;
        else if(i==a&&j==b)qipan[i][j]=0;
        else if(abs(a-i)*abs(b-j)==2)qipan[i][j]=0;
        else if(i==0||j==0)qipan[i][j]=1;
        else qipan[i][j]=qipan[i-1][j]+qipan[i][j-1];
    }

 

 

 

 

 

H:【基本算法—递推递归】几种走法

描述

从原点出发，一步只能向右走、向上走或向左走。恰好走N步且不经过已走的点共有多少种走法？

输入

一个数N。1<=N<=1000。

输出

一个整数，表示共有多少种走法。由于结果可能很大，你只需要输出这个答案mod 12345的值。

样例输入

2

样例输出

7


分析：
我们首先可以清晰的看出，这是一道递推题；
对于递推题，我们应当先求出小数据量，再用计数原理进行数学证明

当n=1时，共有3种不同的走法，即f(1)=3
当n=2时，共有7种不同的走法，即f(2)=7

当n=3时，共有17种不同的走法，即f(3)=17

经过初步观察，我们发现，f(n)=2*f(n-1)+f(n-2);

由此，我们不难看出，对于任何一个起点，最多可以走出3种走法，但最少必须走出2种走法。那么为了求出f(n)，实际上转换为f（n-1）有多少个终点是3种走法，有多少个终点有2种走法的，那么问题就解决了。

有了这样的思路以后，我们不难找到这样的规律：
1.如果f（n-2）存在，即上上步存在，那么从上上步出发的线路里面必然会有一条向上走的线路，而这条向上走的线路在到达f（n-1）之后，  向f（n）出发时也必然有左、上、右这三种走法，那么我们就得出了这样的结论：当f（n-2）存在时，f（n-2）的值实际上就等于f（n-1）有多少个终点是3种走法。

2.用f(n-1)减去f(n-2),也就得到了f(n-1)有多少个终点是2种走法

3.最后我们以f(1)与f(2)为临界值可以得出

f(n)=3*f(n-2)+2*(f(n-1)-f(n-2) ) (n>=3)

化简得f(n)=2*f(n-1)+f(n-2) (n>=3)

 

但是呢，如果使用递归就会超时，所以我最后用递归的思想进行递推

int f(int n){
    int count[1000];
     int r=3,c=1,sum;
     count[0]=1;
     count[1]=3;
     for(int i=2;i<=n;i++){
        count[i]=(2*count[i-1]+count[i-2])%12345;
        }
     return count[n];
}

F：【基本算法—递推递归】计数问题

题目：

描述

在所有的N位数中，有多少个数中有偶数个数字3？

输入

一个数N。1<=N<=1000。

输出

一个整数，所有符合条件数的个数。由于结果可能很大，你只需要输出这个答案mod 12345的值。

样例输入

2

样例输出

73

我们都知道，n位数有10^n-1*9个数，

所以就使用a,b数组分别表示有偶数个3和奇数个3的数的个数；

可以得到a(n）=a(n-1)*9+b(n-1);
因为想要得到偶数的话，

其实就是在所有满足a(n-1)的数字后面加上一个不为三的数，

就是在所有满足b(n-1)的数字后面加上为三的数，

同理得b（n）=b(n-1)*9+a(n-1)

从1位数开始，有9个有偶数个3的数和1个有奇数个3的数；

2位数中，有73个有偶数个3的数和17个有奇数个3的数；
之后即可使用循环；

for(int i=2;i<=n;i++){
                 a[i]=(9*a[i-1]+b[i-1])%12345;
                 b[i]=(9*b[i-1]+a[i-1])%12345;
                 }

至于为何要列举1，2，是因为1中0的情况在2中不适于，属于特殊情况，特殊考虑；

I:〖NOIP2010P〗接水问题

描述

学校里有一个水房，水房里一共装有m 个龙头可供同学们打开水，每个龙头每秒钟的供水量相等，均为1。
现在有n  名同学准备接水，他们的初始接水顺序已经确定。将这些同学按接水顺序从1到n 编号，i 号同学的接水量为wi。接水开始时，1 到m   号同学各占一个水龙头，并同时打开水龙头接水。当其中某名同学j 完成其接水量要求wj 后，下一名排队等候接水的同学k马上接替j   同学的位置开始接水。这个换人的过程是瞬间完成的，且没有任何水的浪费。即j 同学第x 秒结束时完成接水，则k 同学第x+1   秒立刻开始接水。若当前接水人数n’不足m，则只有n’个龙头供水，其它m-n’个龙头关闭。
现在给出n  名同学的接水量，按照上述接水规则，问所有同学都接完水需要多少秒。

输入

第1 行2 个整数n 和m，用一个空格隔开，分别表示接水人数和龙头个数。
第2 行n 个整数w1、w2、……、wn，每两个整数之间用一个空格隔开，wi 表示i 号同学的接水量。

输出

输出只有一行，1 个整数，表示接水所需的总时间。

样例输入

5 3
4 4 1 2 1


8 4
23 71 87 32 70 93 80 76

样例输出

4


163

分析：
这题只需要进行简单的模拟过程即可
第一次我是从头到尾按题意模拟，记录总时间，发现超时了
第二次将所有龙头的时间记录下来，取最长的，还是超时了

经过观察后，我发现：
可以将时间简单的视为一个数据；
每输入一个w，就将当前时间总量最少的水龙头+w；
最后各龙头时间并不相同，输出最大的那个；

 
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>w;
        minv=1;
        for(int j=2;j<=m;j++)
            if(a[j]<a[minv])minv=j;//取最小
        a[minv]+=w;
    }
    int maxv=1;
    for(int i=1;i<=m;i++)
        if(a[i]>a[maxv])maxv=i;//取最大
    cout<<a[maxv];

the end；