[题解]noip杂题题解

Posted 2020-08-10 阿波罗2003

---

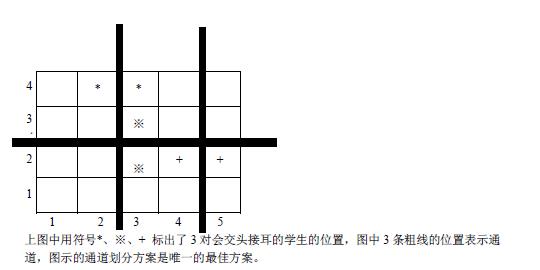
　　这道题没有什么可说的，先统计，然后几次快排，答案就出来了

Code（整齐但不简洁的代码）

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<fstream>
 4 #include<cstring>
 5 #include<queue>
 6 #include<algorithm>
 7 using namespace std;
 8 typedef bool boolean;
 9 template<typename T>
10 inline void readInteger(T& u){
11     char x;
12     while(!isdigit((x = getchar())));
13     for(u = x - \'0\'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - \'0\');
14     ungetc(x, stdin);
15 }
16 int m, n;
17 int k, l;
18 int d;
19 typedef class Point{
20     public:
21         int x;
22         int y;
23         Point(const int x = 0, const int y = 0):x(x), y(y){}
24         boolean operator <(Point another) const{
25             if(this->x != another.x)    return this->x < another.x;
26             return this->y < another.y;
27         }
28 }Point;
29 inline Point readPoint(){
30     Point a;
31     readInteger(a.x);
32     readInteger(a.y);
33     return a;
34 }
35 typedef class MyData{
36     public:
37         int num;
38         int count;
39         MyData(const int num = 0):num(num){}
40 }MyDatas;
41 MyData *c_r;
42 MyData *c_l;
43 inline void init(){
44     readInteger(m);
45     readInteger(n);
46     readInteger(k);
47     readInteger(l);
48     readInteger(d);
49     c_r = new MyData[(const int)(m + 1)];
50     c_l = new MyData[(const int)(n + 1)];
51     memset(c_r, 0, sizeof(MyData) * (m + 1));
52     memset(c_l, 0, sizeof(MyData) * (n + 1));
53     for(int i = 1; i <= m; i++)    c_r[i].num = i;
54     for(int i = 1; i <= n; i++) 　　c_l[i].num = i;
55     for(int i = 1; i <= d; i++){
56         Point a = readPoint();
57         Point b = readPoint();
58         Point s = min(a, b);
59         if(a.x == b.x){
60             c_l[s.y].count++;
61         }else c_r[s.x].count++;
62     }
63 }
64 boolean cmpare(const MyData &a, const MyData &b){
65     return a.count > b.count;
66 }
67 boolean cmpare2(const MyData &a, const MyData &b){
68     return a.num < b.num;
69 }
70 inline void solve(){
71     sort(c_l + 1, c_l + n + 1, cmpare);
72     sort(c_r + 1, c_r + m + 1, cmpare);
73     sort(c_l + 1, c_l + l + 1, cmpare2);
74     sort(c_r + 1, c_r + k + 1, cmpare2);
75     for(int i = 1; i <= k; i++){
76         printf("%d ", c_r[i].num);
77     }
78     putchar(\'\\n\');
79     for(int i = 1; i <= l; i++){
80         printf("%d ", c_l[i].num);
81     }
82 }
83 int main(){
84     freopen("seat.in", "r", stdin);
85     freopen("seat.out", "w", stdout);
86     init();
87     solve();
88     return 0;
89 }

---

---

　　这道题是有依赖的背包问题的裸题，一个主件最多有两个附件，而且附件没有属自己的附件，所以不用考虑树形dp

直接用普通的dp就行了，考虑4个状态

　　1）只要主件

　　2）只要主件和第一个附件

　　3）只要主件和第二个附件

　　4）要主件和它的两个附件

　　如果某个主件的第二个附件不存在呢？不管，不会影响答案，如果特判的话很耗代码。

　　如果dp到附件怎么办？不管，直接跳过

　　如果你希望运行的速度更快，可以将n和每个v除以10，最后结果乘上10

Code（极其不简洁的代码）

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<fstream>
 4 #include<cstring>
 5 #include<queue>
 6 #include<algorithm>
 7 using namespace std;
 8 ///template starts
 9 typedef bool boolean;
10 template<typename T>
11 inline void readInteger(T& u){
12     char x;
13     while(!isdigit((x = getchar())));
14     for(u = x - \'0\'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - \'0\');
15     ungetc(x, stdin);
16 }
17 ///template ends
18 int n;
19 int m;
20 int *v;
21 int *w;
22 int *son[2];
23 int f[3201];
24 int result;
25 boolean *seced;
26 inline void init(){
27     readInteger(n);
28     readInteger(m);
29     n /= 10;
30     v = new int[(const int)(m + 1)];
31     w = new int[(const int)(m + 1)];
32     son[0] = new int[(const int)(m + 1)];
33     son[1] = new int[(const int)(m + 1)];
34     seced = new boolean[(const int)(m + 1)];
35     memset(seced, false, sizeof(boolean) * (m + 1));
36     memset(son[0], 0, sizeof(int) * (m + 1));
37     memset(son[1], 0, sizeof(int) * (m + 1));
38     for(int i = 1, a; i <= m; i++){
39         readInteger(v[i]);
40         v[i] /= 10;
41         readInteger(w[i]);
42         readInteger(a);
43         if(a == 0)    seced[i] = true;
44         if(son[0][a] == 0)    son[0][a] = i;
45         else son[1][a] = i;
46     }
47 }
48 inline void solve(){
49     seced[0] = true;
50     v[0] = w[0] = 0;
51     for(int i = 1; i <= m; i++){
52         if(seced[i]){
53             for(int j = n; j >= v[i]; j--){
54                 f[j] = max(f[j - v[i]] + v[i] * w[i], f[j]);
55                 int s = 0;
56                 int sv = 0;
57                 for(int k = 0; k < 2; k++){
58                     int r = v[son[k][i]] * w[son[k][i]];
59                     s += r;
60                     sv += v[son[k][i]];
61                     if(j >= v[i] + v[son[k][i]]){
62                         f[j] = max(f[j - v[i] - v[son[k][i]]] + v[i] * w[i] + r, f[j]);
63                     }
64                 }
65                 if(j >= v[i] + sv){
66                     f[j] = max(f[j - v[i] - sv] + v[i] * w[i] + s, f[j]);
67                 }
68             }
69         }
70     }
71     printf("%d", f[n] * 10);
72 }
73 int main(){
74     freopen("budget.in", "r", stdin);
75     freopen("budget.out", "w", stdout);
76     init();
77     solve();
78     return 0;
79 }

---

---

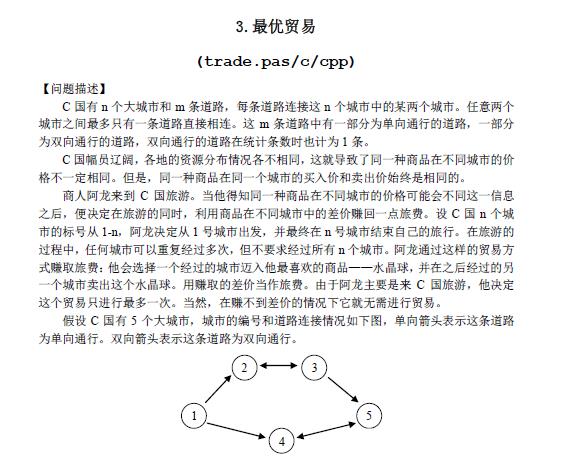
　　这题有两个比较常见的做法，我只写其中一个，但还是都说说

1）Tarjan + 拓扑

　　首先用Tarjan将所有的环（强连通分量）求出来，缩成一个点，求出它的最大值和最小值

接着从起点开始，进行拓扑排序，求出答案

2）spfa

　　首先可以枚举一个断点，为了使答案最大，所以从起点到断点找到一个最小值，再从终点

到起点找到一个最大值，在这个最小值这个点买入，在最大值这个点卖出，用最大值减最小值

求出这个差价。

　　如果每个断点都去跑两次spfa肯定会超时，所以就先用两次spfa预处理，第一次spfa在原

先的图上求出从起点出发，到i这个点的最短“距”，再从反向图中，从终点开始求出到点i这个点

的最长“距”

Code（比较复杂的代码）

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<fstream>
  4 #include<cstring>
  5 #include<queue>
  6 #include<algorithm>
  7 using namespace std;
  8 ///template starts
  9 typedef bool boolean;
 10 template<typename T>
 11 inline void readInteger(T& u){
 12     char x;
 13     while(!isdigit((x = getchar())));
 14     for(u = x - \'0\'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - \'0\');
 15     ungetc(x, stdin);
 16 }
 17 typedef class Edge{
 18     public:
 19         int end;
 20         int next;
 21         Edge(const int end = 0, const int next = 0):end(end), next(next){}
 22 }Edge;
 23 typedef class MapManager{
 24     public:
 25         int ce;
 26         int *h;
 27         Edge *edge;
 28         MapManager():ce(0), h(NULL), edge(NULL){}
 29         MapManager(int limit, int points):ce(0){
 30             h = new int[(const int)(points + 1)];
 31             edge = new Edge[(const int)(limit + 1)];
 32             memset(h, 0, sizeof(int) * (points + 1));
 33         }
 34         inline void addEdge(int from, int end){
 35             edge[++ce] = Edge(end, h[from]);
 36             h[from] = ce;
 37         }
 38 }MapManager;
 39 ///template ends
 40 int n, m;
 41 int getData(boolean (*cmpare)(const int&, const int&), int a, int b){
 42     if((*cmpare)(a, b))    return a;
 43     return b;
 44 }
 45 int *prices;
 46 inline void spfa(MapManager& g, int start, int end, int *f, boolean* visited, boolean (*cmpare)(const int&, const int&)){
 47     memset(visited, false, sizeof(boolean) * (n + 1));
 48     queue<int> que;
 49     que.push(start);
 50     visited[start] = true;
 51     while(!que.empty()){
 52         int u = que.front();
 53         que.pop();
 54         visited[u] = false;
 55         for(int i = g.h[u]; i != 0; i = g.edge[i].next){
 56             int eu = g.edge[i].end;
 57             int d = getData(cmpare, f[u], prices[eu]);
 58             if((*cmpare)(d, f[eu])){
 59                 f[eu] = d;
 60                 if(!visited[eu]){
 61                     que.push(eu);
 62                     visited[eu] = true;
 63                 }
 64             }    
 65         }
 66     }
 67 }
 68 MapManager g;
 69 MapManager rev_g;
 70 int *maxdis;
 71 int *mindis;
 72 boolean *visited;
 73 boolean _min(const int &a, const int &b){    return a < b;    }
 74 boolean _max(const int &a, const int &b){    return a > b;    }
 75 inline void init(){
 76     readInteger(n);
 77     readInteger(m);
 78     g = MapManager(m * 2, n);
 79     rev_g = MapManager(m * 2, n);
 80     prices = new int[(const int)(n + 1)];
 81     maxdis = new int[(const int)(n + 1)];
 82     mindis = new int[(const int)(n + 1)];
 83     visited = new boolean[(const int)(n + 1)];
 84     memset(maxdis, 0, sizeof(int) * (n + 1));
 85     memset(mindis, 0x7f, sizeof(int) * (n + 1));
 86     for(int i = 1; i <= n; i++)
 87         readInteger(prices[i]);
 88     for(int i = 1, a, b, c; i <= m; i++){
 89         readInteger(a);
 90         readInteger(b);
 91         readInteger(c);
 92         g.addEdge(a, b);
 93         rev_g.addEdge(b, a);
 94         if(c == 2){
 95             g.addEdge(b, a);
 96             rev_g.addEdge(a, b);
 97         }
 98     }
 99 }
100 inline void solve(){
101     spfa(g, 1, n, mindis, visited, _min);
102     spfa(rev_g, n, 1, maxdis, visited, _max);
103     int result = 0;
104     for(int i = 2; i < n; i++){
105         result = max(result, maxdis[i] - mindis[i]);
106     }
107     printf("%d", result);
108 }
109 int main(){
110     freopen("trade.in", "r", stdin);
111     freopen("trade.out", "w", stdout);
112     init();
113     solve();
114     return 0;
115 }

（ps：为了防止写两遍spfa，所以一次spfa写得比较复杂）