HDU 2604Queuing

Posted 2020-06-13

题

题意

　　f和m两种字母组成字符串，fmf 和 fff 这种为不安全的字符串，现在有2*L个字母，问你有多少安全的字符串。答案mod M。

分析

　　递推，这题本意是要用矩阵快速幂。不过我发现这题好神奇，只要适当的减少取模的次数，就可以水过去（呵呵呵）。

　　当时做这题的时候用的是比较奇怪的递推式，然后超时了，但是两个两个地推也就水过去了（哈哈哈）。

　　正确的递推方程：f(n)=f(n-1)+f(n-3)+f(n-4)。

　　如果第n位是f，它前面是f时（ff），再前一位必须是m（mff），再前一位还必须是m（mmff），所以有f（n-4）种；

　　　　　　　　　它前面是m时（mf），再前一位必须是m（mmf），再前就任意了，所以有f（n-3）种

　　第n位是m，它前面可以是任意的，所以有f(n-1)种。

　　接下来是构造矩阵：

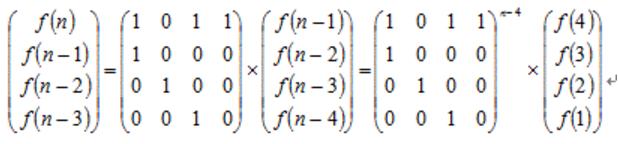
代码

矩阵快速幂代码（AC）

#include<stdio.h>
#include<string.h>
int k,m,t[5]={0,2,4,6,9};
struct matrix
{
    int a[15][15];
    int row,col;
    void init(int row,int col){
        this->row=row;
        this->col=col;
        memset(a,0,sizeof(a));
    }
}u;
struct matrix b{
    {{1,0,1,1},
     {1,0,0,0},
     {0,1,0,0},
     {0,0,1,0}},
    4,4
};
struct matrix c{
    {{9},{6},{4},{2}},
    4,1
};
matrix mul(matrix a,matrix b)
{
    matrix c;
    c.init(a.row,b.col);
    for(int i=0; i<a.row; i++)
        for(int j=0; j<b.col; j++)
            for(int k=0; k<a.col; k++)
                c.a[i][j]=(c.a[i][j]%m+a.a[i][k]*b.a[k][j]%m)%m;
    return c;
}

matrix qpow(matrix a,int k)
{
    matrix ans;
    ans.init(a.row,a.col);
    for(int i=0;i<a.row;i++)
        ans.a[i][i]=1;
    while(k)
    {
        if(k&1)ans=mul(ans,a);
        a=mul(a,a);
        k>>=1;
    }
    return ans;
}

int main()
{
    while(~scanf("%d%d",&k,&m))
    {
        if(k>4){u=mul(qpow(b,k-4),c);
        printf("%d\n",u.a[0][0]%m);}
        else printf("%d\n",t[k]%m);
    }
    return 0;
}

奇怪的姿势一个个推，去掉两个mod就水过去了(AC)

#include<stdio.h>
int l,m,mm,mf,ff,fm,ta,tb,tc,td;
int main()
{
    while(~scanf("%d%d",&l,&m))
    {
        if(l==1)printf("%d\n",2%m);
        else if(l==0)printf("0\n");
        else
        {
            mm=mf=fm=ff=1;
            for(int i=2; i<l; i++)
            {
                ta=mm;
                tb=mf;
                tc=fm;
                td=ff;
                mm=(tc+ta)%m;
                mf=ta;//mf=ta%m;
                fm=(tb+td)%m;
                ff=tb;//ff=tb%m;
            }
            printf("%d\n",(mm+mf+fm+ff)%m);
        }
    }
    return 0;
}

奇怪的姿势两个两个推(AC)

#include<stdio.h>
int l,m;
int mm,mf,fm,ff;
int mma,mfa,fma,ffa;
int i;
int main()
{
    while(~scanf("%d%d",&l,&m))
    {
        if(l==0)printf("0\n");
        else
        {
            if(l%2){
                i=1;
                mm=1;mf=1;fm=0;ff=0;
            }else{
                mm=mf=fm=ff=1;
                i=2;
            }
            for(; i<l; i+=2)
            {
                mma=mm,mfa=mf,fma=fm,ffa=ff;
                mm=(mfa+ffa+fma+mma)%m;
                mf=(fma+mma)%m;
                fm=(mma+mfa)%m;
                ff=mma%m;
            }
            printf("%d\n",(mm+mf+fm+ff)%m);
        }
    }
    return 0;
}

漂亮的直接推(AC)

M(1 <= M <= 30) ，所以只在计算到大于一个比较大的数时才取模，这样可以减少取模的次数。这是参考了别人的代码。

#include<stdio.h>

int l,m;
int f[1000005]={0,2,4,6,9};

int main()
{
    while(~scanf("%d%d",&l,&m))
    {
        for(int i=5;i<=l;i++){

            f[i]=f[i-1]+f[i-3]+f[i-4];

            if(f[i]>1000000)
                f[i]%=m;
        }
        printf("%d\n",f[l]%m);
    }
    return 0;
}