二分图匹配--匈牙利算法

Posted 2020-08-09 一只有恒心的小菜鸟

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了二分图匹配--匈牙利算法相关的知识，希望对你有一定的参考价值。

二分图匹配--匈牙利算法

二分图匹配

匈牙利算法

基本定义：

二分图 —— 对于无向图G=(V,E)，如果存在一个划分使V中的顶点分为两个互不相交的子集，且每个子集中任意两点间不存在边 ?∈E,则称图G为一个二分图。

二分图的充要条件是，G至少有两个顶点，且所有回路长度为偶数。

匹配 —— 边的集合，其中任意两条边都不存在公共顶点。
匹配边即是匹配中的元素，匹配点是匹配边的顶点，同样非匹配边，非匹配点相反定义。

最大匹配——在图的所有匹配中，包含最多边的匹配成为最大匹配
完美匹配——如果在一个匹配中所有的点都是匹配点，那么该匹配称为完美匹配。

附注：所有的完美匹配都是最大匹配，最大匹配不一定是完美匹配。假设完美匹配不是最大匹配，那么最大匹配一定存在不属于完美匹配中的边，而图的所有顶点都在完美匹配中，不可能找到更多的边，所以假设不成立，及完美匹配一定是最大匹配。

交替路——从一个未匹配点出发，依次经过非匹配边，匹配边，非匹配边…形成的路径称为交替路，交替路不会形成环。

增广路——起点和终点都是未匹配点的交替路。
因为交替路是非匹配边、匹配边交替出现的，而增广路两端节点都是非匹配点，所以增广路一定有奇数条边。而且增广路中的节点(除去两端节点)都是匹配点，所属的匹配边都在增广路径上，没有其他相连的匹配边，因此如果把增广路径中的匹配边和非匹配边的“身份”交换，就可以获得一个更大的匹配(该过程称为改进匹配)。

示例图

Fig1_09_09.JPG

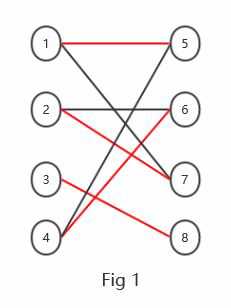
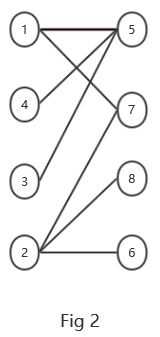
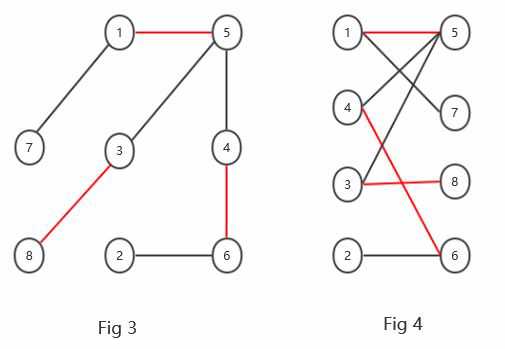
注释：

Fig3是一个二分图G=(V,E),V={1,2,3,4,5,6,7,8},E={(1,7),(1,5),(2,6),(3,5),(3,8),(4,5),(4,6)},该图可以重绘成Fig4，V可分成两个子集V={V1,V2},V1={1,2,3,4},V2={5,6,7,8}。
Fig4中的红色边集合就是一个匹配{(1,5),(4,6),(3,8)}
Fig2中是最大匹配
Fig1中红色边集合是完美匹配
Fig1中交替路举例(4-6-2-7-1-5)
Fig4中增广路(2-6-4-5-1-7)

匈牙利树

匈牙利树中从根节点到叶节点的路径均是交替路，且匈牙利树的叶节点都是匹配点。
匈牙利算法
求解最大匹配的算法，通过不断的寻找增广路径，并将增广路径进行改进匹配，直至找不到更多的增广路径。
二分图的最大匹配可以通过匈牙利树的搜索寻找增广路径来获得，而树的搜索可以使用深度优先搜索(DFS)或者广度优先搜索(BFS)
下面使用matlab代码实现DFS和BFS下的匈牙利算法：

function Hungarian(c1, m, IsDraw) 
% 匈牙利算法寻找无向二分图的最大匹配 
% inputs: 
% -AdjTable     顶点元素的邻接表，cell结构，每一个元素是一个一维数组， 
%               保存对应节点的邻接节点编号 
% -c1           第一个顶点子集元素个数 
% -m            搜索方法,‘B‘是广度优先搜索，‘D’是深度优先搜索 
% -IsDraw        是否绘图 
 
if nargin<2 
    m=‘B‘; 
    IsDraw=0; 
elseif nargin<3 
    IsDraw=0; 
end 
 
global MatTable Check AdjTable 
% -MatTable     匹配表，长度为顶点个数，每个元素存放该节点所在匹配边的另一端节点 
%               的编号；如果是非匹配点，则对应值为0 
cn=length(AdjTable);%顶点个数 
MatTable=zeros(1,cn);% 默认都是未匹配点 
Check = zeros(1,cn); % 覆盖过的点不能再访问，否则死循环 
 
EdgesNum=0;% 最大匹配中元素个数 
if m==‘D‘ % 深度优先搜索 
    if c1<cn-c1 
        for i=1:c1 
            if DFS(i) 
                EdgesNum=EdgesNum+1; 
            end 
        end 
    else 
        for j=c1+1:cn 
            if DFS(j) 
                EdgesNum=EdgesNum+1; 
            end 
        end     
    end 
else % 广度优先搜索 
    EdgesNum = BFS(c1);   
end 
fprintf(‘There is %f edges in the biggest matches.\n‘,EdgesNum); 
if IsDraw 
    c2=cn-c1; 
    X1=ones(c1,1)*40; 
    Y1=20:10:c1*10+19; 
    X2=ones(c2,1)*100; 
    Y2=20:10:c2*10+19; 
    X=[X1;X2]; 
    Y=[Y1‘;Y2‘]; 
    color={‘ro:‘,‘ko:‘}; 
    for i=1:cn 
        if MatTable(i)~=0 
            plot(X(i),Y(i),color{1},‘MarkerSize‘,15);hold on   
            if i<=c1 
                text(X(i)-3,Y(i),num2str(i)); 
            else 
                text(X(i)+3,Y(i),num2str(i)); 
            end 
        else 
            plot(X(i),Y(i),color{2},‘MarkerSize‘,15);hold on 
            if i<c1 
                text(X(i)-3,Y(i),num2str(i)); 
            else 
                text(X(i)+3,Y(i),num2str(i)); 
            end 
        end 
    end 
    for i=1:cn 
        for j=1:length(AdjTable{i}) 
            if MatTable(i)==AdjTable{i}(j) 
                plot(X([i,AdjTable{i}(j)]),Y([i,AdjTable{i}(j)]),‘r.-‘,‘LineWidth‘,2);hold on 
            else 
                plot(X([i,AdjTable{i}(j)]),Y([i,AdjTable{i}(j)]),‘k.-‘,‘LineWidth‘,2);hold on 
            end 
        end 
    end 
    box(‘on‘) 
    axis off 
    hold off 
 
end 
 
 
end 
% AdjTable 邻接表 
% MatTable 匹配表 
function bool=DFS(u) 
% n 是左侧未匹配点的编号 
% 寻找节点n的一条未匹配边 
global AdjTable MatTable Check 
for i=1:length(AdjTable{u}) 
    v=AdjTable{u}(i); 
    if ~Check(v) 
        Check(v)=1; 
        if MatTable(v) == 0|| DFS(MatTable(v))  
            %v是未匹配点则找到增广路径，交换身份 
            %否则，如果v的匹配点存在增广路径, 
            %那么也是找到一条增广路径 
            % || 是短路运算符 
            MatTable(u) = v; 
            MatTable(v) = u; 
            bool=1; 
            return;              
        end   
    end 
end 
bool=0; 
end 
 
function EdgeNum=BFS(c1) 
global AdjTable MatTable Check 
pre = zeros(length(AdjTable))-1; 
% 存放的是该点所在的非匹配边的前一个非匹配边的右端端点编号 
queue=[];% 广度优先搜索需要的搜索队列 
EdgeNum=0;%最大匹配元素个数 
for i=1:c1 
    if ~MatTable(i) % 寻找未匹配点 
        queue=[i];%入队列 
        flag = 0; % 未找到增广路径 
        pre(i)=-1; % 为了最后改进路径时设定终点  
        while(~isempty(queue)&&~flag) 
            u=queue(1); 
            queue(1)=[];%出队列 
            edges=AdjTable{u}; 
            for j=1:length(edges) 
                v = edges(j); 
                if ~flag && Check(v)~=i 
                    Check(v)=i; 
                    queue=[queue,MatTable(v)]; 
                    %找到一条匹配路，将匹配路的右端节点放入队列 
                    if MatTable(v) % 非增广路 
                        pre(MatTable(v))=u; 
                        %下一条非匹配边的起点对应前一条非匹配边的起点 
                    else % 找到增广路径 
                        flag=1; 
                        d=u; 
                        e=v; 
                        while d~=-1 
                            t = MatTable(d); 
                            MatTable(d)=e; 
                            MatTable(e)=d; 
                            d = pre(d); 
                            e = t; 
                        end 
                    end 
                end 
            end 
        end 
    end 
        if MatTable(i)~=0 %表示找到增广路径了，此时起点肯定在匹配边上 
            EdgeNum=EdgeNum+1; 
        end 
end 
end 
 
 
function testHungarian 
c1=5; 
c2=5; 
% AdjMatrix=randi(2,c1,c2)-1; 
t=0.7; 
AdjMatrix=rand(c1,c2)>t; 
% AdjMatrix=ones(c1,c2); 
global AdjTable 
AdjTable = cell(c1+c2,1); 
for i=1:c1 
    t=find(AdjMatrix(i,:)~=0); 
    AdjTable{i}=c1+t; 
end 
for j=1:c2 
    t=find(AdjMatrix(:,j)~=0); 
    AdjTable{c1+j}=t; 
end 
 
Hungarian(c1,‘B‘,1); 
end 
 

分析：
参考的blog中指出算法的时间复杂度为,实际应用中使用BFS的算法比DFS算法更快，但是在matlab代码中，发现使用DFS算法的搜索比BFS算法搜索的速度快不少，尤其是顶点和边数比较大的情形。

参考文献
Renfei Song‘s Blog
百度百科-二分图

以上是关于二分图匹配--匈牙利算法的主要内容，如果未能解决你的问题，请参考以下文章

匈牙利算法dfs模板 [二分图][二分图最大匹配]