聚类算法

Posted 2020-08-09 dataAlpha

一、聚类算法简介

聚类是无监督学习的典型算法，不需要标记结果。试图探索和发现一定的模式，用于发现共同的群体。有时候作为监督学习中稀疏特征的预处理。有时候可以作为异常值检测（反欺诈中有用）。

应用场景：新闻聚类、用户购买模式（交叉销售）、图像与基因技术

相似度与距离：这个概念是聚类算法中必须明白的，简单来说就是聚类就是将相似的样本聚到一起，而相似度用距离来定义，聚类是希望组内的样本相似度高，组间的样本相似度低，这样样本就能聚成类了。常用三类距离（余弦距离比较难收敛，优势是不受原来样本线性变换影响）：

聚类算法分类：基于位置的聚类（kmeans\kmodes\kmedians）层次聚类（agglomerative\birch）基于密度的聚类（DBSCAN）基于模型的聚类（GMM\基于神经网络的算法）

二、Kmeans算法

1.确定聚类个数K 

2.选定K个D维向量作为初始类中心 

3.对每个样本计算与聚类中心的距离，选择最近的作为该样本所属的类 

4.在同一类内部，重新计算聚类中心（几何重心） 不断迭代，直到收敛：

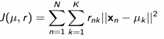（损失函数）每个样本到聚类中心的距离之和或平方和不再有很大变化。

缺点：1.对初始聚类中心敏感，缓解方案是多初始化几遍，选取损失函数小的。2.必须提前指定K值（指定的不好可能得到局部最优解），缓解方法，多选取几个K值，grid search选取几个指标评价效果情况3.属于硬聚类，每个样本点只能属于一类 4.对异常值免疫能力差，可以通过一些调整（不取均值点，取均值最近的样本点）5.对团状数据点区分度好，对于带状不好（谱聚类或特征映射）。尽管它有这么多缺点，但是它仍然应用广泛，因为它速度快，并且可以并行化处理。

缺失值问题：离散的特征：将缺失的作为单独一类，90%缺失去掉。连续的特征：其他变量对这个变量回归，做填补；样本平均值填补；中位数填补。

三、层次聚类算法

有自顶而下和自底向上两种，只是相反的过程而已，下面讲自顶而下的思路。

1.计算所有个体和个体之间的距离，找到离得最近的两个样本聚成一类。

2.将上面的小群体看做一个新的个体，再与剩下的个体，计算所有个体与个体之间距离，找离得最近的两个个体聚成一类，依次类推。

3.直到最终聚成一类。

群体间的距离怎么计算呢？

 

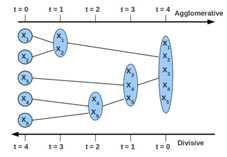
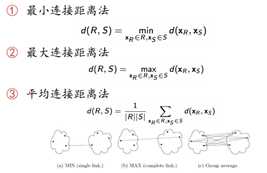
缺点：虽然解决了层次聚类中Kmeans的问题，但计算量特别大。与Kmeans相比两者的区别，除了计算速度，还有kmeans只产出一个聚类结果和层次聚类可根据你的聚类程度不同有不同的结果。

四、GMM（混合高斯模型）

属于软聚类（每个样本可以属于多个类，有概率分布）GMM认为隐含的类别标签z(i)，服从多项分布，并且认为给定z(i)后，样本x(i)满足多值高斯分布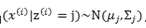，，由此可以得到联合分布。

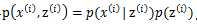GMM是个鸡生蛋、蛋生鸡的过程，与KMEANS特别像，其估计应用EM算法。

1.首先假设知道GMM参数，均值、协方差矩阵、混合系数，基于这些参数算出样本属于某一类的概率（后验概率）wji：

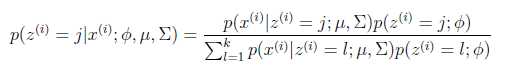
 2.然后根据该概率，重新计算GMM的各参数。此参数求解利用了最大似然估计。

 

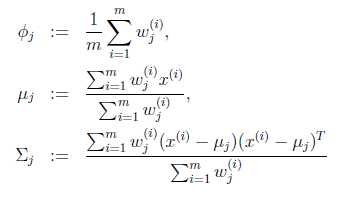
3.一直迭代，直到参数稳定。

EM（Expectation Maximization）算法是，假设我们想估计知道A和B两个参数，在开始状态下二者都是未知的，但如果知道了A的信息就可以得到B的信息，反过来知道了B也就得到了A。可以考虑首先赋予A某种初值，以此得到B的估计值，然后从B的当前值出发，重新估计A的取值，这个过程一直持续到收敛为止。

混合高斯模型，实质上就是一个类别一个模型。先从k个类别中按多项式分布抽取一个z(i)，然后根据z(i)所对应的k个多值高斯分布中的一个生成样本x(i)，整个过程称作混合高斯模型。

GMM优点：可理解、速度快  劣势：初始化敏感、需要手工指定k（高斯分布）的个数、不适合非凸分布数据集（基于密度的聚类和核方法可以处理）

Kmeans可以看做混合高斯聚类在混合成分方差相等、且每个样本派给一个混合成分时的特例。

五、部分应用经验

可以先对样本进行基于其分布的抽样，然后在小样本范围内进行层次聚类，然后用层次聚类得出的K值，应用于整个样本进行Kmeans聚类。

聚类分析结果评价：

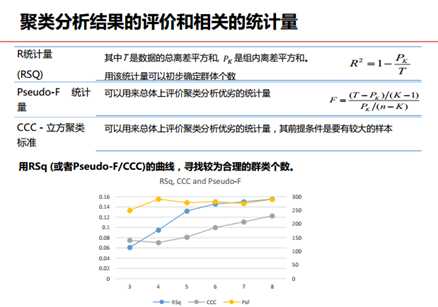
建模步骤：1.变量预处理：缺失值、异常值（用p1或P99替代）、分类变量变成数值型、分类变量转为哑变量、分类变量过多  这里涉及一系列recoding的过程。2.变量标准化：变量的量纲不一样会引起计算距离的差距。3.变量的筛选:商业意义、多个维度、变量间相关性。4.确定分类个数：区分性足够好，又不能太细