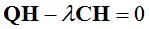圆的拟合(带拉格朗日乘子)
Posted LeonHuo
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了圆的拟合(带拉格朗日乘子)相关的知识,希望对你有一定的参考价值。
圆弧特征如图1所示。圆弧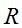 的特征向量为R:
[φR, ρR, r]T,其中φR为圆心极角,φR ~ N(μφR,σφR2);ρ为圆心极径,ρR ~ N(μρR,σρR2);
的特征向量为R:
[φR, ρR, r]T,其中φR为圆心极角,φR ~ N(μφR,σφR2);ρ为圆心极径,ρR ~ N(μρR,σρR2);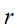 为圆半径,r~N(μr,σr2)。圆弧极坐标公式为:
为圆半径,r~N(μr,σr2)。圆弧极坐标公式为:
其中,x = [xi, yi]T,a = 1,b = [-2ρRcosφR, -2ρRsinφR]T,c=ρR2-r2。将上式整理为矩阵形式:
其中,H=[1,b(1,1), b(2,1),c]T,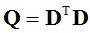 ,
, 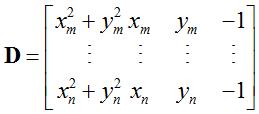 。由于b2(1,1)+ b2(2,1)-4c=4r2,引入拉格朗日乘子λ,得:
。由于b2(1,1)+ b2(2,1)-4c=4r2,引入拉格朗日乘子λ,得:
其中,Q为正定矩阵,待求特征向量H一定对应绝对值最小特征值λ。圆弧特征θ=arctan(H(2,1)/H(1,1)), 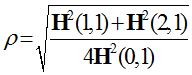 ,
,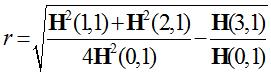 。
。
以上是关于圆的拟合(带拉格朗日乘子)的主要内容,如果未能解决你的问题,请参考以下文章
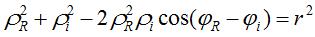

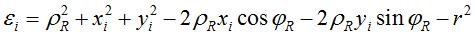
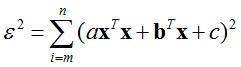
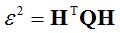
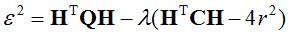
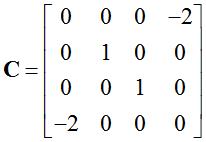 。满足
。满足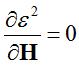 得:
得: