拉格朗日乘子法
Posted ZSYL
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了拉格朗日乘子法相关的知识,希望对你有一定的参考价值。
拉格朗日乘子法
拉格朗日乘子法 (Lagrange multipliers)是⼀种寻找多元函数在⼀组约束下的极值的方法.
通过引入拉格朗日乘子,可将有 d 个变量与 k 个约束条件的最优化问题转化为具有 d + k 个变量的⽆约束优化问题求解。本文希望通过⼀个直观简单的例子尽力解释拉格朗日乘⼦法和KKT条件的原理。
以包含⼀个变量⼀个约束的简单优化问题为例。

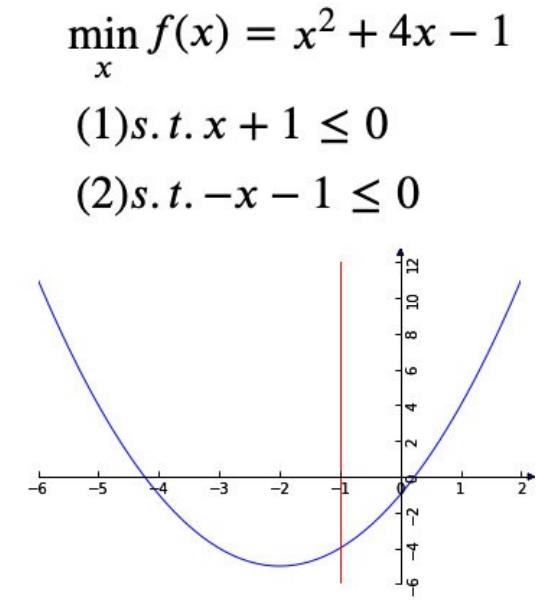
我们可以直观的从图中得到,
- 对于约束 1) 使目标值f(x)最小的最优解是x=−2;
- 对于约束 2) 使目标值f(x)最小的最优解是x=−1。
下面我们用拉格朗日乘子来求解这个最优解。

以上是关于拉格朗日乘子法的主要内容,如果未能解决你的问题,请参考以下文章