四轴之互补滤波与四元数算法最详细分析

Posted 2020-08-07 公众号：硬件工程师看海

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了四轴之互补滤波与四元数算法最详细分析相关的知识，希望对你有一定的参考价值。

有人问我关于四元数姿态解算算法的分析，每次都解释好久，今日空闲，特发一帖，供大家参考。本分析将结合程序，分析姿态解算思路，由于能力有限，难免有错误之处请谅解，同时希望能够抛砖引玉，得到大神指点。感谢圆点博士提供资料参考。

为尊重原创，转载请注明原出处，谢谢。

http://blog.csdn.net/u013608300/article/details/52459515

微信公众号：工程师看海

四轴之互补滤波与四元数算法最详细分析

原创：冰三点水

关键字：姿态解算互补滤波四元数

下面进入正题。

第一部分传感器说明

通常我们开源小四轴使用mpu6050姿态传感器，可以输出三轴加速度和三轴角速度数据。角速度数据就是x、y、z三个轴的旋转角速度。而加速度是沿三个轴的加速度，这个加速度计测量的是比力。这里对于加速度计有个重点，我们想象这样一个模型，在太空中有一个盒子，盒子里连着三轴弹簧，力感应球位于弹簧连接点，在外太空失重时，三条弹簧伸缩量为0，x = y = z= 0；

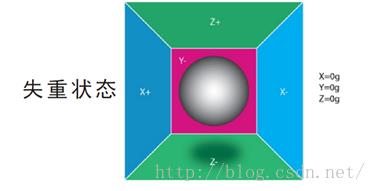
当在重力场内，盒子静置与地面时，力感应球收到重力的吸引孤儿有一个轴的弹簧有伸缩变化，或者说当盒子（加速度计）静置时会有一个输出，大小等于重力，这就是我们说的比力。（感谢第七实验室的图片）

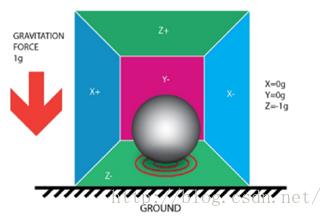
在互补滤波算法中，我们认为四轴是平滑运动，也就是说我们忽略了加速度计测量的和运动带来的影响，而认为加速度计测量的就是重力（比力）不包括和运动，这是互补滤波是局限性所在，补偿方法请自行分析。（感谢投笔从容提供思路）

实际上，我们单单通过三轴角速度就可以得到四元数，进而将四元数转换成欧拉角，也就是姿态角，问题是陀螺仪会有积分漂移，得到的角度会有误差，这时候我们就引入加速度计对陀螺仪数据进行校正，以得到更准确的角度。不过这时yaw，也会存在误差，在误差不能忽略的使用情况下，我们就需要用磁力计了。

第二部分四元数

二维平面内的旋转可以用复数表示（即a+bi），三维空间内的旋转需要用四元数（即a+bi+cj+dk）来表示，而不是我们猜测的类似于三元数（a+bi+cj）表示。注意四元数表示的是一个旋转。相比于复数，四元数也有类似与i的虚部，所以它其实是超复数。四元数的转化成三角形式可以看出它描述了刚体的定点运动（见秦永元惯性导航四元数相关章节），当只关心v系相对于R系的角位置时，可以认为是b系到R系经过一次等效旋转而成的。四元数Q包含了等效旋转的全部信息。注意，描述刚体旋转的四元数是规范化四元数，也就是说四元数的范数（模）等于1！！！！！！这就是为什么引入误差向量后，四元数要重新归一化。（如果我们得到了四元数，只要通过一个公式就可以将四元数转换到欧拉角，得到我们需要的姿态。那么怎么得到四元数呢？

我们常听说四元数微分方程，这个方程的输入是角速度数据，我们只要输入角速度数据，就可以更新四元数数据。

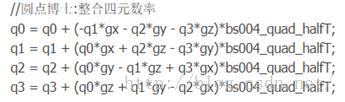
上图为程序实现的对四元数微分方程的解。这个方程是怎么来的呢？由于机体的运动，四元数Q也是变化的，换句话说，q0 q1 q2q3是时间的函数。我们把四元数写成三角形式，

即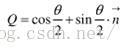

这里有角度量，然后对这个式子进行求导，然后进行一下相应的转换，这里提供一个四路，细节就不讲了。上面的程序是解这个方程的常用方法。

第三部分四元数到欧拉角

四元数到欧拉角有公式，对于一个固定的欧拉角旋转顺序有相应的公式。程序上实现起来比较容易

程序中的57.3是个转换系数，是弧度和角度的转换系数。

这个公式具体请参考秦永元老师的惯性导航。

第四部分互补滤波

到目前为止，我们已经可以通过四元数微分方程得到四元数，在通过四元数到欧拉角的转换得到四轴的姿态，但是为了得到更加准确的姿态，我们引入了加速度计。

在IMU程序中我们刚开始看到的往往是将加速度原始数据归一化。

归一化后的ax、ay、az的平方和为1，各自方向不变，也就是合向量的方向不变，模等于1，这是个重点。

建立小四轴坐标系

这个很简单，所谓的建立小四轴坐标系不过是把世界坐标系下的重力向量（0 0 1）转换到小四轴坐标系下而已，换句话说，小四轴坐标系相对于世界坐标系是运动的，而重力向量在世界坐标系是｛0 0 1｝，那么它在小四轴坐标系下是多少呢？这就通过这个旋转矩阵*Rb来求得。图就不画了，有想要的@我。

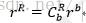
R为小四轴坐标系，b为世界坐标系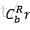，是方向余弦矩阵

这个方向余弦矩阵是怎么来的呢？

请参考惯性导航或下面链接（请诸位一定阅读相关内容，起码下面的连接解释了旋转矩阵的由来）

http://www.doc88.com/p-893241688972.html

互补滤波这个部分到目前为止还没进入正题。（楼主已经写的好烦啊。。。。。。）

目前的进度是建立了小四轴坐标系。

接下来是重点！

将刚才转移到小四轴坐标系下的重力向量和机体加速度计测量的重量向量叉乘！

得到一个误差向量。这个误差向量是有物理意义的。叉乘等于|A|*|B|*sin(角度),转移到小四轴坐标系的重力向量模为1，加速度计测量的重力向量经过归一化也为1，那么叉乘的结果只与角度有关，并且角度越大，误差向量的莫越大！归一化的目的在这里体现。向量的叉乘还包括方向信息，还是一个向量，有人认为，在固定的采样计算时间内的按一定方向转过这些误差向量，也可以看作成角速度（来自黑暗骑士）这读者自己揣摩吧。总之，我们就是通过这个误差向量来修正陀螺仪数据的。