组合数学 04 - 基本计数问题

Posted 2020-08-06 万物皆数

1. 基本计数

1.1 统一模型

　　本篇来讨论几个基本的计数问题，这些问题虽然都有各自的模型，但本质上却有着内在的联系，因此我们先建立一个统一的模型。现在有元素集\\(E,F\\)，它们的元素都有内在的结构，建立映射\\(E\\to F\\)，问题是这样的映射有多少个？满射和单射有多少个？

　　所谓有内在的结构，就是元素间的拓扑结构，我们所说的映射个数，严格讲是在拓扑同构意义下的等价类的个数。拓扑结构种类繁多，无法一一研究，本篇只探讨两个基本的拓扑结构，下一篇会做更一般性的讨论。这个模型虽然对本章作用有限，但可以从更高的视角思考看待问题的本质，而且各个问题间联系也一目了然。

　　两个基本拓扑结构分别是：无序结构和有向链表。无序结构中的元素是离散的、无差别的，在拓扑同构下可以互相替换。有向链表中的元素是完全区分的，它的拓扑同构只有自身，当然只有自身的拓扑结构不止这一个，这里只要强调完全区分性，所谓有向链表可以当做是给每个元素编了号。以下设\\(E,F\\)都是有限集，且记\\(|E|=m,|F|=n\\)。

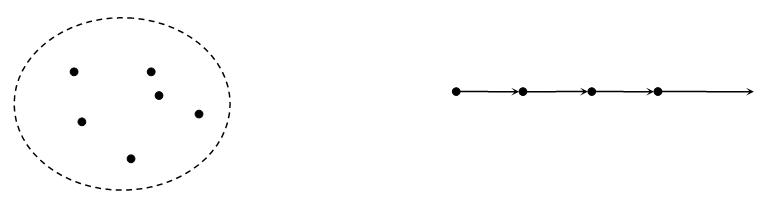
1.2 模型1：可区分\\(\\to\\)可区分

　　可完全区分的结构比较简单，先来看\\(E,F\\)都是有向链表的情况，\\(E,F\\)分别纵向排列，\\(E\\to F\\)就是一般的函数定义。对\\(E\\)的每个元素都有\\(n\\)个值可以映射，由乘法原理便知映射一共有\\(n^m\\)种。这个结构有一个更常用、更直观的模型，考察由\\(n\\)个字母组成的集合\\(S\\)，用这些字母组成长度为\\(m\\)的单词\\(x_1x_2\\cdots x_m\\)。这个单词也被称\\(S\\)上的\\(m\\)元可重复排列，或\\(m\\)元字。不难证明它和模型1的等价性，故\\(S\\)上的\\(m\\)元字有\\(n^m\\)个。

　　现在对映射添加一些限制，比如假设\\(E\\)的第\\(k\\)个元只能取某\\(n_k\\)个值，由乘法定理知可以有\\(n_1n_2\\cdots n_m\\)个\\(m\\)元字。再限制每个元素的映射不能相同，或者说字中没有重复字母，第\\(k\\)个元素只能取\\(n-k+1\\)个值。这其实就是我们熟悉的\\(n\\)个元素中选\\(m\\)个元素的排列数\\(P(n,m)\\)（式（1）），其中表达式\\(x(x-1)\\cdots(x-k+1)\\)简记为\\((x)_k\\)，也叫做\\(x\\)的降\\(k\\)阶乘（\\(x\\)不要求是自然数）。类似地记表达式\\(x(x+1)\\cdots(x+k-1)\\)简记为\\((x)^k\\)，也叫做\\(x\\)的升\\(k\\)阶乘。

\\[P(n,m)=(n)_m=n(n-1)\\cdots(n-m+1)=\\dfrac{n!}{(n-m)!}\\tag{1}\\]

　　排列数要求每个函数值最多被映射一次，继续推广，我们假定\\(F\\)中第\\(k\\)个数被映射\\(m_k\\)次。这样的字称为是\\(a_1^{m_1}a_2^{m_2}\\cdots a_n^{m_n}\\)型字，其中\\(m_1+m_2+\\cdots+m_n=m\\)。先将\\(m_k\\)个字母\\(a_k\\)看成互异的字母\\(a_{k1},\\cdots,a_{km_k}\\)，这样的字有\\(m!\\)个，而原来的每个字对应到\\(m_1!m_2!\\cdots m_n!\\)个这样的字，故有式（2）成立。

\\[N(a_1^{m_1}a_2^{m_2}\\cdots a_n^{m_n})=\\dfrac{m!}{m_1!m_2!\\cdots m_n!}\\tag{2}\\]

　　• 求\\(S\\)上的相邻字母不相同的\\(m\\)元字的个数。

1.3 模型2：不可区分\\(\\to\\)可区分

　　现在假定\\(E\\)是无序的，而\\(F\\)是有向链表，由于原像不可区分，要关注的便是像的组合情况。它的一个等价模型我们也很熟悉：从\\(n\\)种颜色的球里选出\\(m\\)个球。如果要求每种颜色只能选一个，相当于映射为单射，选取个数称为\\(n\\)的\\(m\\)元不重复组合数，记作\\(\\binom{n}{m}\\)，一般也简称为组合数。它其实就是排列在\\(E\\)无序下的等价类的个数，具体说就是\\(m!\\)个排列属于同一个等价类，故有公式（3）。

\\[\\binom{n}{m}=\\dfrac{(n)_m}{m!}=\\dfrac{n!}{m!(n-m)!}\\tag{3}\\]

　　如果颜色可以重复选，选取个数称为\\(n\\)的\\(m\\)元可重复组合数，记作\\(\\left(\\binom{n}{m}\\right)\\)。设每个像被映射的次数为\\(x_k\\)，可重复组合数等价于方程（4）的非负整数解的个数。对这个问题，有两个比较巧妙的方法，它们都把可重复组合问题转化为了不重复组合问题，其中的对应思想是非常重要的。一种方法是直接理解方程（4），它相当于把\\(m\\)个相同的元素分割为可区分的\\(n\\)份。将\\(m\\)个元素一字排开，在其中插入\\(n-1\\)个隔板即可，隔板和元素共\\(m+n-1\\)个位子，我们就是要选择其中的\\(n-1\\)个位置，这就有式（5）成立。

\\[x_1+x_2+\\cdots+x_n=m\\tag{4}\\]

\\[\\left(\\binom{n}{m}\\right)=\\binom{m+n-1}{m}=\\dfrac{(n)^m}{m!}\\tag{5}\\]

　　另一种解释式（4）的方法也非常经典，考察\\(s_k=x_1+\\cdots+x_k\\)组成的单调递增序列（式（6）左），\\(s_k\\)在\\([n]\\)中取值，但可能存在重复值。为了消除等号，再令\\(t_k=s_k+k-1\\)，这时有式（6）成立，其中\\(t_k\\)在\\([m+n-1]\\)中取互异值，同样得到公式（5）。利用这个思想，更容易得到不等式（7）的非负整数解为\\(\\binom{m+n}{m}\\)，它也相当于左式分别取\\(0\\sim m\\)时的解数和，故有式（8）成立。

\\[0\\leqslant s_1\\leqslant\\cdots\\leqslant s_n=m\\;\\Leftrightarrow\\;0\\leqslant t_1<\\cdots<t_n=m+n-1,\\;t_k=s_k+k-1\\tag{6}\\]

\\[x_1+x_2+\\cdots+x_n\\leqslant m\\tag{7}\\]

\\[\\sum_{k=0}^m\\binom{n+k-1}{k}=\\binom{n+m}{m}\\tag{8}\\]

　　• \\([n]\\)中取\\(m\\)个互不相邻的数，求取法个数。

1.4 模型3：可区分\\(\\to\\)不可区分

　　像不可区分，就好比\\(n\\)个相同的篮子，把可区分的原像看做是\\(m\\)个不同的球，问题等价于：\\(m\\)个不同的球放进\\(n\\)个篮子的方法。根据有球的篮子数\\(k\\)，问题被分为\\(n\\)种情况，每一种情况都是相同的问题：\\(m\\)个球分成\\(k\\)堆的分法。我们就集中研究这个问题，而\\(m\\)个元素分成\\(k\\)部分的个数被称为第二类Stirling数，记作\\(S(m,k)\\)。

　　Stirling数并没有简单的表达式，我们先从它的递推关系入手，这也是组数计算问题的常用方法。考察某个元素\\(a_1\\)，分割后有两种情况：它单独分为一堆，或和其它元素在一堆。所以很容易有递推关系（9）。使用递推关系归纳，可以得到比较漂亮的公式（10），如果你觉得正向证明不明显，可以试试反向证明。

\\[S(m,k)=S(m-1,k-1)+kS(m-1,k)\\tag{9}\\]

\\[S(k+r,k)=\\sum_{1\\leqslant k_1\\leqslant k_2\\leqslant\\cdots\\leqslant k_r\\leqslant k}k_1k_2\\cdots k_r\\tag{10}\\]

　　考虑模型3和模型1的关系，模型3中的1个分割是模型1中的一个等价类：被映射的像的个数为\\(k\\)。这个等价类中有\\(\\binom{n}{k}k!=(n)_k\\)个元素（先选\\(k\\)个像再排列），从而我们有重要的关系式（11）（\\(S(m,0)=0\\)）。\\(m\\)个元素的总分割数被称为Bell数，记作\\(B_m\\)，它显然是式（12）左。以某个元素所在堆的大小分类讨论，容易有递推关系式（12）右。

\\[n^m=\\sum_{k=0}^nS(m,k)(n)_k\\tag{11}\\]

\\[B_m=\\sum_{k=0}^mS(m,k)\\;\\Rightarrow\\;B_{m+1}=\\sum_{k=0}^m\\binom{m}{k}B_{m-k}\\tag{12}\\]

1.5 模型4：不可区分\\(\\to\\)不可区分

　　当原像和像都不可区分时，只需关心分割的堆数和每堆的个数，等价的模型就是整数\\(m\\)的分拆数\\(p(n)\\)。对应地分拆为\\(k\\)部分的个数记作\\(p(m,k)\\)，它表示不定方程（13）正整数解的个数，注意它和方程（4）的区别在于不考虑分拆的顺序。既然不考虑各部分的顺序，每个分拆其实还对应方程（14）的一组非负整数解。

\\[x_1+x_2+\\cdots+x_k=m,\\;\\;(x_1\\geqslant x_2\\geqslant\\cdots\\geqslant x_k)\\tag{13}\\]

\\[x_1+2x_2+3x_3+\\cdots+mx_m=m\\tag{14}\\]

　　分拆数同样没有简单的表达式，我们还是先来建立一些递推关系式。根据\\(x_k\\)是否为\\(1\\)可得到递推关系（15），持续使用该式便得到式（16），它也有显然的组合意义。

\\[p(m,k)=p(m-1,k-1)+p(m-k,k)\\tag{15}\\]

\\[p(k+r,k)=p(r,1)+p(r,2)+\\cdots+p(r,k)\\tag{16}\\]

　　关于\\(m\\)的某个分拆结果\\(x_1,x_2,\\cdots,x_k\\)，有个直观的表示方法，以点表示不可区分的元素，在第\\(i\\)行排列\\(x_i\\)个点。比如\\((5,5,3,2)\\)画成下图，这样的图称为菲勒（Ferrers）示意图，利用其直观性可以得到很多意想不到的结论。菲勒图纵横翻转后仍然是菲勒图，它对应的分拆称为原分拆的共轭分拆，对于分拆\\(\\pi\\)，其共轭分拆一般记作\\(\\pi^*\\)。从菲勒图中容易得到：（1）\\(p(m,k)\\)等于\\(m\\)最大分部为\\(k\\)的分拆数；（2）\\(m\\)最多\\(k\\)个部分的分拆数，等于\\(m\\)最大分部不大于\\(k\\)的分拆数。

　　满足\\(\\pi=\\pi^*\\)的分拆称为自共轭分拆，它的菲勒图沿对角线对称。将其菲勒图按如图所示分割，便知\\(m\\)的自共轭分拆数等于各部分是不同奇数的分拆数。再看各部分都不同的分拆，每个部分\\(x_k\\)都可以唯一地表示为\\(i\\cdot 2^j\\)，其中\\(i\\)为奇数。把该部分拆分为\\(2^j\\)个\\(i\\)，最终得到所有部分为奇数的分拆。反之对各部分为奇数的分拆，因为大小为\\(i\\)的部分的个数可以唯一表示为\\(2\\)的幂次之和，故这个对应关系是双向的。这就是说，各部分不相等的分拆数等于各部分为奇数的分拆数。

2. 基本计数的性质

2.1 二项式系数

　　前面我们已经讨论过，组合数\\(\\binom{n}{m}\\)是\\((1+x)^n\\)展开式中\\(x^m\\)项的系数，当然也二项式（17）中\\(x^my^{n-m}\\)项的系数，故它也称为二项式系数。组合数的定义式（3）中，\\(\\dfrac{n!}{m!(n-m)!}\\)要求\\(m,n\\)都是非负整数，但\\(\\dfrac{(n)_m}{m!}\\)中\\(n\\)可以为任何实数，以后形式\\(\\binom{x}{m}\\)也可以用来表示多项式\\(\\dfrac{(x)_m}{m!}\\)。这个推广其实是合理的，而在微积分中我们知道\\((1+x)^{\\alpha}\\)的幂级数展开式如式（18）所示（牛顿二项式定理），它正是\\((1+x)^n\\)的推广。另外易知，可重复组合数还可以写成式（19）。

\\[(x+y)^n=\\sum_{k=0}^n\\binom{n}{k}x^ky^{n-k}\\tag{17}\\]

\\[(1+x)^{\\alpha}=1+\\sum_{k=1}^{\\infty}\\binom{\\alpha}{k}x^k\\tag{18}\\]

\\[\\left(\\binom{n}{m}\\right)=(-1)^m\\binom{-n}{m}\\tag{19}\\]

　　在中学我们就知道一些二项式系数的性质，证明都不难，这里仅仅列举。式（20）中分别是对称性和递推性，其中递推性有显然的组合意义。式（21）是随\\(m\\)的变化体现出来的单峰性。\\((1+x)^n\\)中令\\(x=\\pm 1\\)可得式（22）和（23），另外利用\\((1+x)^m(1+x)^n=(1+x)^{m+n}\\)可得范德蒙恒等式（Vandermonde）（24）。

\\[\\binom{n}{m}=\\binom{n}{n-m};\\;\\;\\binom{n}{m}=\\binom{n-1}{m-1}+\\binom{n-1}{m}\\tag{20}\\]

\\[\\binom{n}{0}<\\binom{n}{1}<\\cdots<\\binom{n}{\\lfloor\\frac{n}{2}\\rfloor}=\\binom{n}{\\lceil\\frac{n}{2}\\rceil}>\\cdots>\\binom{n}{n}\\tag{21}\\]

\\[\\binom{n}{0}+\\binom{n}{1}+\\cdots+\\binom{n}{n}=2^n\\tag{22}\\]

\\[\\binom{n}{0}+\\binom{n}{2}+\\binom{n}{4}+\\cdots=\\binom{n}{1}+\\binom{n}{3}+\\binom{n}{5}+\\cdots=2^{n-1}\\tag{23}\\]

\\[\\sum_{k=0}^r\\binom{m}{k}\\binom{n}{r-k}=\\binom{m+n}{r}\\tag{24}\\]

　　二项式系数很早就被研究，最著名的当然就是杨辉三角（帕斯卡三角），它正是利用了公式（20）右。在反演公式那一章我们已经知道，矩阵\\(\\{a_{ij}=\\binom{i}{j}\\}\\)的逆矩阵是\\(\\{b_{ij}=(-1)^{i-j}\\binom{i}{j}\\}\\)，故有式（25）成立，当然你也可以直接证明它。

\\[\\sum_{k=0}^n(-1)^{k+m}\\binom{n}{k}\\binom{k}{m}=\\delta_{mn}=\\left\\{\\begin{matrix}1,&\\text{if}\\;m=n\\\\0,&\\text{if}\\;m\\ne n\\end{matrix}\\right.\\tag{25}\\]

　　• 证明：\\(\\sum\\limits_{k=0}^n\\binom{n}{k}^2=\\binom{2n}{n}\\)；

　　• 证明：\\(\\binom{n}{1}+2\\binom{n}{2}+\\cdots+n\\binom{n}{n}=n\\cdot 2^{n-1}\\)；

　　• 写出\\((x_1+x_2+\\cdots+x_p)^n\\)的展开式。

2.2 Stirling数

　　现在继续讨论第二类Stirling数，从名字就知道它是个有故事的数。公式（10）并不能让人满意，它甚至只是另一个计数问题的描述而已，能使用的就只有公式（11）了。该式显然满足单链\\(L_m\\)的反演公式的形式，把它整理为式（25）左式（为了得到关联函数\\(\\binom{n}{k}\\)），由反演公式得到了式（25）右，从而有\\(S(n,k)\\)的另一个显式表达式（26）。

\\[n^m=\\sum_{k=0}^n\\binom{n}{k}k!S(m,k)\\;\\Leftrightarrow\\;n!S(m,n)=\\sum_{k=0}^n(-1)^{n-k}\\binom{n}{k}k^m\\tag{25}\\]

\\[S(m,k)=\\dfrac{1}{k!}\\sum_{i=0}^k(-1)^{k-i}\\binom{k}{i}k^m\\tag{26}\\]

　　由于公式（11）对任意\\(n\\leqslant m\\)成立，故有等式（27）左成立，从而\\(S(m,k)\\)给出了多项式组\\(\\{x^m\\}\\)和\\(\\{(x)_m\\}\\)的线性表出关系。这样的线性表出必定有逆关系（式（27）右），其中的\\(s(m,k)\\)就被称为第一类Stirling数，它和第一类Stirling数有关系式（28）。

\\[x^m=\\sum_{k=0}^mS(m,k)(x)_k\\;\\Leftrightarrow\\;(x)_m=\\sum_{k=0}^ms(m,k)x^k\\tag{27}\\]

\\[\\sum_{k=0}^mS(m,k)s(k,n)=\\delta_{nm}=\\left\\{\\begin{matrix}1,&\\text{if}\\;m=n\\\\0,&\\text{if}\\;m\\ne n\\end{matrix}\\right.\\tag{28}\\]

　　另一方面，考察式（27）右，不难知道\\(s(m,k)\\)有递推式（29），类似地有表达式（30）。\\(s(m,k)\\)正负项交叉出现，为了寻找其组合意义，考察表达式（31）中的\\(c(m,k)\\)。它显然是\\(s(m,k)\\)的绝对值，并且满足式（32）。容易验证，含有\\(k\\)个轮换的\\(m\\)元置换数，也满足式（32）的递推关系，这便是它的组合意义。

\\[s(m,k)=s(m-1,k-1)-(m-1)s(m-1,k)\\tag{29}\\]

\\[s(k+r,k)=(-1)^r\\sum_{1\\leqslant k_1\\leqslant k_2\\leqslant\\cdots\\leqslant k_r\\leqslant k+r}k_1k_2\\cdots k_r\\tag{30}\\]

\\[(x)^m=\\sum\\limits_{k=0}^mc(m,k)x^k\\tag{31}\\]

\\[c(m,k)=c(m-1,k-1)+(m-1)c(m-1,k)\\tag{32}\\]

　　• 求\\(1^{\\lambda_1}2^{\\lambda_2}\\cdots m^{\\lambda_m}\\)型置换的个数。