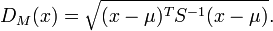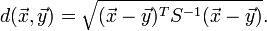paper 114：Mahalanobis Distance(马氏距离)

(from:http://en.wikipedia.org/wiki/Mahalanobis_distance)

 

Mahalanobis distance

In statistics, Mahalanobis distance is a distance measure introduced by P. C. Mahalanobis in 1936.It is based on correlations between variables by which different patterns can be identified and analyzed. It gauges similarity of an unknown sample set to a known one. It differs fromEuclidean distance in that it takes into account the correlations of the data set and is scale-invariant. In other words, it is a multivariateeffect size.

Definition

Formally, the Mahalanobis distance of a multivariate vector 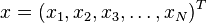 from a group of values with mean  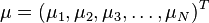and covariance matrix  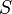is defined as:

(注：1.这个是X和总体均值的马氏距离。2.这里的S是可逆的，那么协方差矩阵不可逆的话怎么办？)

Mahalanobis distance (or "generalized squared interpoint distance" for its squared value) can also be defined as a dissimilarity measure between two random vectors  and  of the same distribution with the covariance matrix  :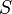

If the covariance matrix is the identity matrix, the Mahalanobis distance reduces to the Euclidean distance. If the covariance matrix is diagonal, then the resulting distance measure is called the normalized Euclidean distance:

where 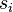 is the standard deviation of the  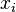（ ） over the sample set.

(源自：百度百科)

马氏优缺点：

1.马氏距离的计算是建立在总体样本的基础上的，这一点可以从上述协方差矩阵的解释中可以得出，也就是说，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同。

 

2.在计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧式距离计算即可。

 

3.还有一种情况，满足了条件总体样本数大于样本的维数，但是协方差矩阵的逆矩阵仍然不存在，比如三个样本点(3,4),(5,6)和(7,8)这种情况是因为这三个样本在其所处的二维空间平面内共线。这种情况下，也采用欧式距离计算。

 

4.在实际应用中“总体样本数大于样本的维数”这个条件是很容易满足的，而所有样本点出现3）中所描述的情况是很少出现的，所以在绝大多数情况下，马氏距离是可以顺利计算的，但是马氏距离的计算是不稳定的，不稳定的来源是协方差矩阵，这也是马氏距离与欧式距离的最大差异之处。

 　　

优点：它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关；由标准化数据和中心化数据(即原始数据与均值之差）计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。

 

缺点：它的缺点是夸大了变化微小的变量的作用。