Linear regression with one variable算法实例讲解(绘制图像,cost_Function ,Gradient Desent, 拟合曲线, 轮廓图绘制)_矩阵操作(代码片
Posted 豆子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Linear regression with one variable算法实例讲解(绘制图像,cost_Function ,Gradient Desent, 拟合曲线, 轮廓图绘制)_矩阵操作(代码片相关的知识,希望对你有一定的参考价值。
%测试数据 \'ex1data1.txt\', 第一列为 population of City in 10,000s, 第二列为 Profit in $10,000s
1 6.1101,17.592 2 5.5277,9.1302 3 8.5186,13.662 4 7.0032,11.854 5 5.8598,6.8233 6 8.3829,11.886 7 7.4764,4.3483 8 8.5781,12 9 6.4862,6.5987 10 5.0546,3.8166 11 5.7107,3.2522 12 14.164,15.505 13 5.734,3.1551 14 8.4084,7.2258 15 5.6407,0.71618 16 5.3794,3.5129 17 6.3654,5.3048 18 5.1301,0.56077 19 6.4296,3.6518 20 7.0708,5.3893 21 6.1891,3.1386 22 20.27,21.767 23 5.4901,4.263 24 6.3261,5.1875 25 5.5649,3.0825 26 18.945,22.638 27 12.828,13.501 28 10.957,7.0467 29 13.176,14.692 30 22.203,24.147 31 5.2524,-1.22 32 6.5894,5.9966 33 9.2482,12.134 34 5.8918,1.8495 35 8.2111,6.5426 36 7.9334,4.5623 37 8.0959,4.1164 38 5.6063,3.3928 39 12.836,10.117 40 6.3534,5.4974 41 5.4069,0.55657 42 6.8825,3.9115 43 11.708,5.3854 44 5.7737,2.4406 45 7.8247,6.7318 46 7.0931,1.0463 47 5.0702,5.1337 48 5.8014,1.844 49 11.7,8.0043 50 5.5416,1.0179 51 7.5402,6.7504 52 5.3077,1.8396 53 7.4239,4.2885 54 7.6031,4.9981 55 6.3328,1.4233 56 6.3589,-1.4211 57 6.2742,2.4756 58 5.6397,4.6042 59 9.3102,3.9624 60 9.4536,5.4141 61 8.8254,5.1694 62 5.1793,-0.74279 63 21.279,17.929 64 14.908,12.054 65 18.959,17.054 66 7.2182,4.8852 67 8.2951,5.7442 68 10.236,7.7754 69 5.4994,1.0173 70 20.341,20.992 71 10.136,6.6799 72 7.3345,4.0259 73 6.0062,1.2784 74 7.2259,3.3411 75 5.0269,-2.6807 76 6.5479,0.29678 77 7.5386,3.8845 78 5.0365,5.7014 79 10.274,6.7526 80 5.1077,2.0576 81 5.7292,0.47953 82 5.1884,0.20421 83 6.3557,0.67861 84 9.7687,7.5435 85 6.5159,5.3436 86 8.5172,4.2415 87 9.1802,6.7981 88 6.002,0.92695 89 5.5204,0.152 90 5.0594,2.8214 91 5.7077,1.8451 92 7.6366,4.2959 93 5.8707,7.2029 94 5.3054,1.9869 95 8.2934,0.14454 96 13.394,9.0551 97 5.4369,0.61705
%绘制实际数据图像——人口和利润的关系图 fprintf(\'Plotting Data ...\\n\') data = load(\'ex1data1.txt\'); X = data(:, 1); y = data(:, 2); m = length(y); % number of training examples % Plot Data % Note: You have to complete the code in plotData.m plotData(X, y); fprintf(\'Program paused. Press enter to continue.\\n\'); pause;
1 %plotData()函数实现 2 3 function plotData(x, y) 4 5 figure; % open a new figure window 6 plot(x, y, \'rx\', \'MarkerSize\', 10); %Set the size of Points(\'MarkerSize\', 10) 7 ylabel(\'profit in $10,1000s\'); 8 xlabel(\'population of City in 10,000s\'); 9 10 end
1 %% =================== Part 3: Gradient descent 2 3 fprintf(\'Running Gradient Descent ...\\n\') 4 5 X = [ones(m, 1), data(:,1)]; % Add a column of ones to x 6 7 theta = zeros(2, 1); % initialize fitting parameters 8 9 % Some gradient descent settings 10 iterations = 1500; %迭代次数 11 alpha = 0.01; %learning rate 12 13 % compute and display initial cost 14 computeCost(X, y, theta) %y是真实的值
1 % Compute Cost for linear regression 2 % cost Function函数实现___利用矩阵操作进行!! 3 function J = computeCost(X, y, theta) 4 5 % Initialize some useful values 6 m = length(y); % number of training examples 7 J = 0; 8 9 % Instructions: Compute the cost of a particular choice of theta 10 % You should set J to the cost. 11 12 % X = [ ones(m, 1), data(:, 1) ], theta = [ th1; th2] 13 predictions = X * theta; %矩阵操作--预测函数 14 sqrError = (predictions - y).^2; 15 J = sum(sqrError) / (2*m); 16 17 end
1 %运行梯度下降算法 2 % run gradient descent 3 4 theta = gradientDescent(X, y, theta, alpha, iterations); 5 6 % print theta to screen 7 fprintf(\'Theta found by gradient descent: \'); 8 fprintf(\'%f %f \\n\', theta(1), theta(2));
1 %梯度下降算法实现 gradientDescent(X, y, theta, alpha, iterations)
%X-training example,y-实际数值,alpha-learning rate 2 function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters) 3 4 % theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by 5 % taking num_iters gradient steps with learning rate alpha 6 7 % Initialize some useful values 8 m = length(y); % number of training examples 9 J_history = zeros(num_iters, 1); 10 11 for iter = 1:num_iters 12 predictions = X * theta; %预测值h(xi)--利用了矩阵运算 13 sqrError = (predictions - y); %预测值 - 实际值 14 15 % Simultaneously update(同时更新thetaj) thetaj for all j. 16 % alpha - learning rate, \'.*\'---是内积(矩阵对应元素相乘) 17 theta1 = theta(1) - alpha * (1/m) * sum(sqrError .* X(:,1)); 18 theta2 = theta(2) - alpha * (1/m) * sum(sqrError .* X(:,2)); 19 theta(1) = theta1; 20 theta(2) = theta2; 21 22 23 % Save the cost J in every iteration 24 J_history(iter) = computeCost(X, y, theta); 25 26 %disp(J_history); %增加输出语句,方便调试 27 28 end 29 30 end
1 %绘制拟合曲线 2 % Plot the linear fit 3 hold on; % keep previous plot visible 4 plot(X(:,2), X*theta, \'-\') 5 legend(\'Training data\', \'Linear regression\') %添加图例 6 hold off % don\'t overlay any more plots on this figure
1 % Predict values for population sizes of 35,000 and 70,000 2 %利用求出的拟合参数--预测新值,利用矩阵运算 3 predict1 = [1, 3.5] *theta; 4 fprintf(\'For population = 35,000, we predict a profit of %f\\n\',... 5 predict1*10000); 6 7 predict2 = [1, 7] * theta; 8 fprintf(\'For population = 70,000, we predict a profit of %f\\n\',... 9 predict2*10000); 10 11 fprintf(\'Program paused. Press enter to continue.\\n\'); 12 pause;
1 %计算不同 theta参数下, J(θ)值的变化, 绘制图像 2 %% ============= Part 4: Visualizing J(theta_0, theta_1) ============= 3 4 fprintf(\'Visualizing J(theta_0, theta_1) ...\\n\') 5 6 % Grid over which we will calculate J 7 %linspace(x, y, n)--在(x,y)区间内均匀生成n个数 8 theta0_vals = linspace(-10, 10, 100); 9 theta1_vals = linspace(-1, 4, 100); 10 11 % initialize J_vals to a matrix of 0\'s 12 J_vals = zeros(length(theta0_vals), length(theta1_vals)); 13 14 % Fill out J_vals 15 for i = 1:length(theta0_vals) 16 for j = 1:length(theta1_vals) 17 t = [theta0_vals(i); theta1_vals(j)]; 18 J_vals(i,j) = computeCost(X, y, t); 19 end 20 end 21 22 23 % Because of the way meshgrids work in the surf command, we need to 24 % transpose J_vals before calling surf, or else the axes will be flipped 25 26 J_vals = J_vals\'; 27 % Surface plot 28 figure; 29 30 %surf(X,Y,Z)--creates the surface plot from corresponding(对应值) value in X, Y,Z (default: color is proportional(成正比) to surface height.) 31 32 surf(theta0_vals, theta1_vals, J_vals) 33 xlabel(\'\\theta_0\'); ylabel(\'\\theta_1\');
1 % Contour plot----轮廓图的绘制 2 figure; 3 4 % Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100 5 6 contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20)) 7 xlabel(\'\\theta_0\'); ylabel(\'\\theta_1\'); 8 hold on; 9 plot(theta(1), theta(2), \'rx\', \'MarkerSize\', 10, \'LineWidth\', 2);
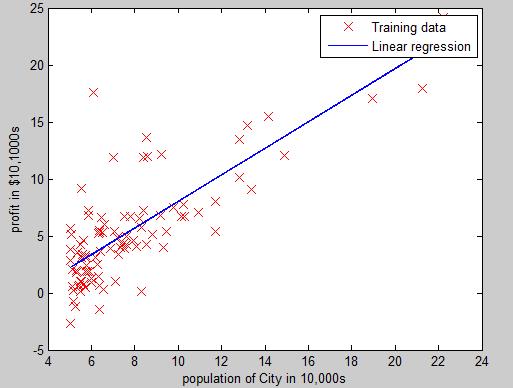
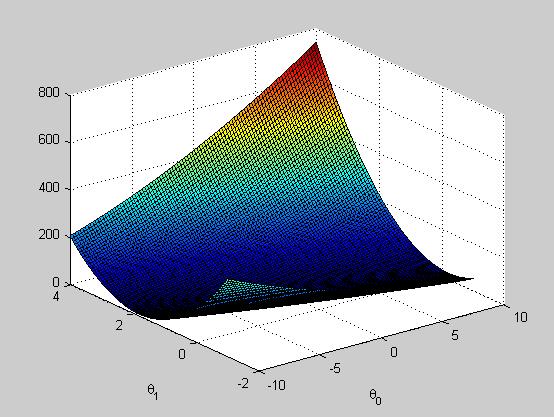
 绘图效果如上。
绘图效果如上。
以上是关于Linear regression with one variable算法实例讲解(绘制图像,cost_Function ,Gradient Desent, 拟合曲线, 轮廓图绘制)_矩阵操作(代码片的主要内容,如果未能解决你的问题,请参考以下文章
Linear Regression with PyTorch
Coursera《machine learning》--单变量线性回归(Linear Regression with One Variable)
Linear regression with one variable - Model representation
机器学习笔记-1 Linear Regression with Multiple Variables(week 2)
Coursera - machine learning Linear regression with one variable-quiz