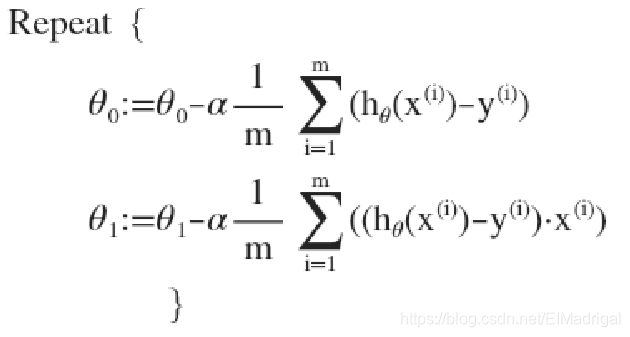#Week2 Linear Regression with One Variable

Posted 2020-11-25 eimadrigal

一、Model Representation

还是以房价预测为例，一图胜千言：

h表示一个从x到y的函数映射。

二、Cost Function

因为是单变量线性回归，所以假设函数是：
[h_{ heta}(x)= heta_0+ heta_1x]
所以接下来的问题是怎样确定参数( heta_0)和( heta_1)？
这两个参数会决定我们的模型预测值与训练集的实际数据的差距，这就是建模误差。
那么在回归问题中，代价函数选择如下的平方误差函数比较合理：
[J( heta_0, heta_1)=frac{1}{2m}sum_{i=1}^{m}(h_{ heta}(x^{(i)})-y^{(i)})^2]
m是训练集的样本数目，(x^{(i)})是每个房子的尺寸，(y^{(i)})是实际价格。
只要寻找使得(J( heta_0, heta_1))最小的参数即可。
之所以要除以2，主要是为了后续的梯度下降法求导时抵消平方的那个2。

三、Gradient Descent

为了求得代价函数的最小值，采用梯度下降法。

• 用一个随机的参数组合计算(J)
• 找到一个使得(J)下降最多的参数组合，更新参数，直到找到一个局部最优解

就像下山一样，每次都走一步，每次选择下降最快的方向直到局部最低。
在批量梯度下降算法（所有的训练样本都要用到）中，同步更新所有参数：

(alpha)是学习率，表示每一步走多长。
如果(alpha)太小，那么更新的过程就会很缓慢；如果(alpha)太大，可能跳过最低点，导致发散。
当接近局部最优时，由于斜率会越来越小，所以每一步会自动走得很小，不需要减小学习率(alpha)。

四、Gradient Descent For Linear Regression

对之前得回归模型应用梯度下降算法：
对(J( heta_0, heta_1))求关于( heta_0)、( heta_1)的偏导数，带入参数更新公式，有：