1. 基本思想
在第一篇中,我们讨论了lanczos算法的基本框架。当我们用lanczos算法将一个实对称阵转化成三对角阵之后,我们可以用第二篇中的QR算法计算三对角阵的特征值特征向量。
本篇我们将讨论计算该三对角阵更加快速的算法——分治法(Divide and Conquer),该算法最早由Cuppen于1981年提出。
给定实对称三对角阵
$T=\\left(\\begin{matrix}\\alpha_1 & \\beta_1 & & & \\dots\\\\ \\beta_1 & \\alpha_2 & \\beta_2 & & \\dots \\\\ & \\beta_2 &\\alpha_3 & \\beta_3 & \\dots \\\\ & & & & \\dots \\end{matrix}\\right)$
分治法的基本思想是将T分成两块三对角阵,求得这两块三对角阵的特征值特征向量之后,再合并,求合并之后的特征值特征向量:
分(Divide):
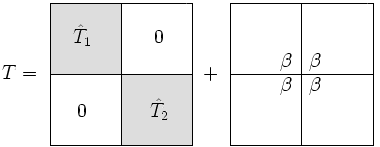
求$\\hat{T_1},\\hat{T_2}$的特征值分解:
$\\hat{T_1}=Q_1 D_1 Q^T_1$
$\\hat{T_2}=Q_2 D_2 Q^T_2$
合并(Conquer)
T可以表示为:
$T=\\left(\\begin{matrix}Q_1 & \\\\ & Q_2\\end{matrix}\\right)(D+\\beta zz^T) \\left(\\begin{matrix}Q^T_1 & \\\\ & Q^T_2\\end{matrix}\\right)$
其中,$D=\\left(\\begin{matrix}D_1 & \\\\ & D_2\\end{matrix}\\right), z^{{T}}=(q_{{1}}^{{T}},q_{{2}}^{{T}})$, $q_{{1}}^{{T}}$是$Q_{{1}}$的最后一行, $q_{{2}}^{{T}}$是$Q_{{2}}$的第一行
现在要求T的特征值分解,$T=Q \\Lambda Q^T$,可以先求$D+\\beta zz^T$的特征值分解 $D+\\beta zz^T=P \\Lambda P^T$,再令$Q=\\left(\\begin{matrix}Q_1 & \\\\ & Q_2\\end{matrix}\\right)P$
如何求$D+\\beta zz^T$ 的特征值分解呢?如果$\\beta=0$则显然P=I。下面假设$\\beta\\ne 0$
假设$\\lambda\\ne 0$是特征值,$p\\ne 0$是对应的特征向量,根据特征值定义我们有
$(D+\\beta zz^T)p=\\lambda p$
$(D-\\lambda I)p + \\beta zz^Tp=0$
$p + (D-\\lambda I)^{-1}\\beta zz^Tp=0$
$z^Tp + z^T(D-\\lambda I)^{-1}\\beta zz^Tp=0$
假如D所有对角线元素各不相同,并且z的所有元素不为0 (这两个假设来自wiki,但是感觉没什么道理,anyway先pass)。可以证明$z^Tp\\ne 0$。
反证法,否则$(D+\\beta zz^T)p=Dp = \\lambda p$,p是D的特征向量。因为D对角线元素各不相同,因此p只能有一个非0分量,而由于z所有分量非0,所以得到$z^Tp\\ne 0$
由此我们有
$1 + \\beta z^T(D-\\lambda I)^{-1} z=0$
或者写成如下形式:
$1 + \\beta \\sum_i \\frac{z_i^2}{d_i-\\lambda}=0$
其中$d_i = D_{ii}$
因此求特征值问题最后归结为求解一个方程的根。这个方程被称为"Secular Equation"。 该方程的解法下面会详细讨论,这里略过。得到特征值之后,根据 上面第二行 $(D-\\lambda I)p + \\beta zz^Tp=0$,可以得出$(D-\\lambda I)^{-1}z$是特征值$\\lambda$对应的特征向量。
至此我们得到了分治法的框架,总结如下:
[Q,D] = DivideAndConquer(T)
//输入T实对称三对角阵,输出T的特征值分解T=Q D Q\',Q为正交阵,每列为T的特征向量,D为对角阵,对角线元素为T的特征值
if T is 1x1 matrix
Q=1, D=T
else
Divide

[Q1,D1]=DivideAndConquer($\\hat{T_1}$)
[Q2,D2]=DivideAndConquer($\\hat{T_2}$)
let $D=\\left(\\begin{matrix}D_1 & \\\\ & D_2\\end{matrix}\\right), z^{{T}}=(q_{{1}}^{{T}},q_{{2}}^{{T}}), Q_{{1}}$的最后一行和$Q_{{2}}$的第一行拼接成的向量
Find eigen values $\\lambda=[\\lambda_1, \\lambda_2 \\dots ]^T$ of $D+\\beta zz^T$ by solving Secular Equation
$1 + \\beta \\sum_i \\frac{z_i^2}{d_i-\\lambda}=0$
Calculate corresponding eigen vectors
$p_i=(D-\\lambda_i I)^{-1}z$
Update eigen vectors of T:
$Q=\\left(\\begin{matrix}Q_1 & \\\\ & Q_2\\end{matrix}\\right)P$
where $P=[p_1,p_2,\\dots ]$
return D=diag($\\lambda$), Q
end
2. Secular Equation的解法
这节讨论secular方程$1 + \\beta \\sum_{i=1}^n \\frac{z_i^2}{d_i-\\lambda}=0$的解法,这里假设$\\forall i, z_i \\ne 0,\\qquad \\forall i\\ne j, d_i\\ne d_j$
任选一个i,作变量代换:
$\\lambda = d_i + \\beta \\mu$
$\\delta_j=\\frac{d_j-d_i}{\\beta}$
这样secular方程就变为
$h_i(\\mu)=1 + \\sum_{i=j}^n \\frac{z_j^2}{\\delta_j-\\mu}=0$
这个方程有n个根,且根各不相同,按照从小到大的顺序,记这n个根为$\\mu_1< \\mu_2 < \\dots <\\mu_n$。
不失一般性,假设$\\delta_1< \\delta_2 < \\dots < \\delta_{i-1} < 0=\\delta_{i} < \\delta_{i+1} < \\dots <\\delta_n$,则有 $\\delta_j < \\mu_j < \\delta_{j+1}$, 对于j=n的情况,$\\delta_n < \\mu_n < +\\infty =\\delta_{n+1}$
举个例子,函数$h_3(\\mu) = 1+\\frac{0.1}{-2-\\mu}+\\frac{0.5}{-0.5-\\mu}+\\frac{0.2}{-\\mu}+\\frac{0.2}{1-\\mu}+\\frac{0.4}{2-\\mu}$的图像如下
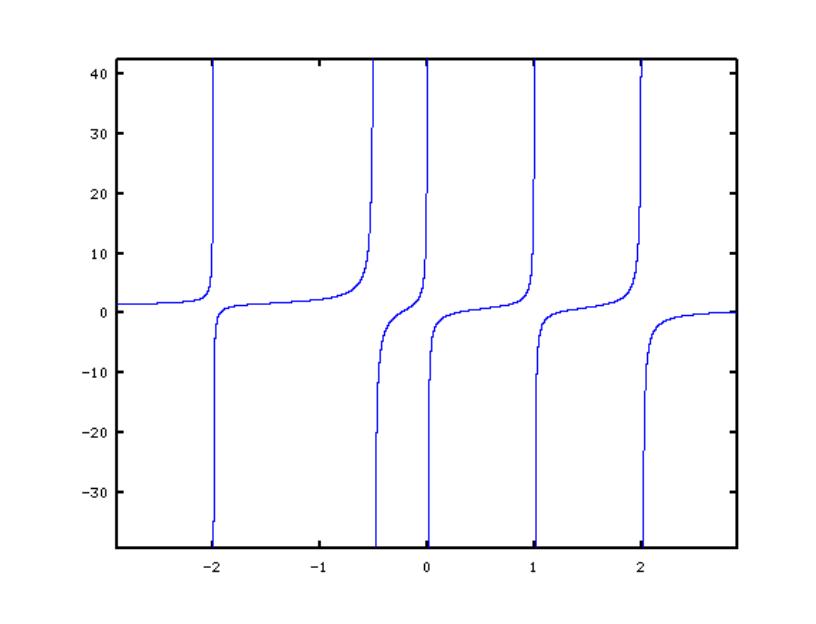
可以看到$0 < \\mu_i < \\delta_{i+1}$, 我们可以在区间$(0,\\delta_{i+1})$内求解第i个根。我们把这个区间放大,得到如下图像。
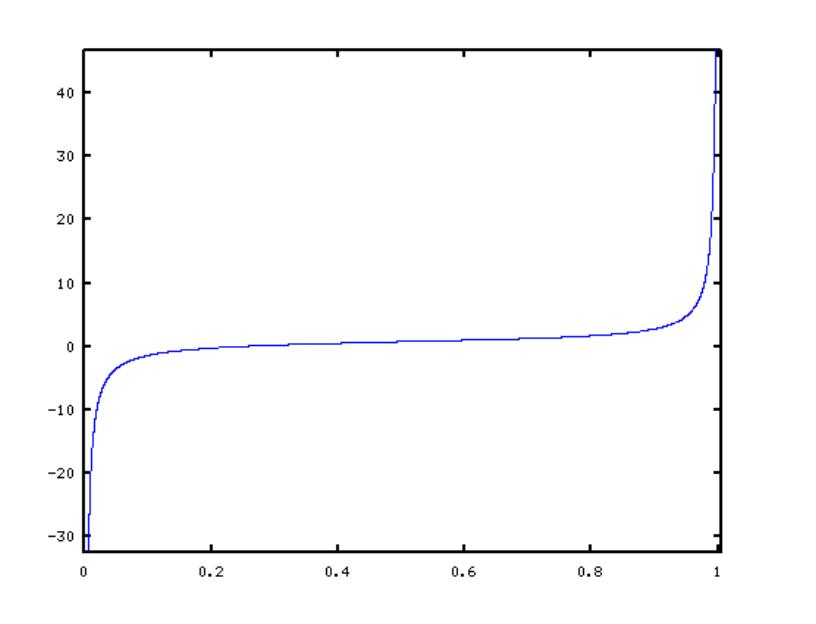
可以看到这段区间内,函数h单调增,与x轴有1个交点。如何求这个点呢,最简单的是2分法,可以在log时间内收敛。
更快的是牛顿迭代法。但是这里注意一个问题,就是如果初始点选的不好,牛顿法会发散,找不到根。如何保证牛顿法收敛呢?这里我们需要对变量作一个替换,
令$\\gamma=\\frac1{\\mu}$
这样,原来的定义域$0<\\mu_i<\\delta_{i+1}$就变成了$\\gamma_i>\\frac1{\\delta_{i+1}}$,对于i=n的情况,$\\gamma_n>0$
现在我们看一下新的函数$h_i(\\gamma)$在区间$(\\frac1{\\delta_{i+1}},\\infty)$上的图像.
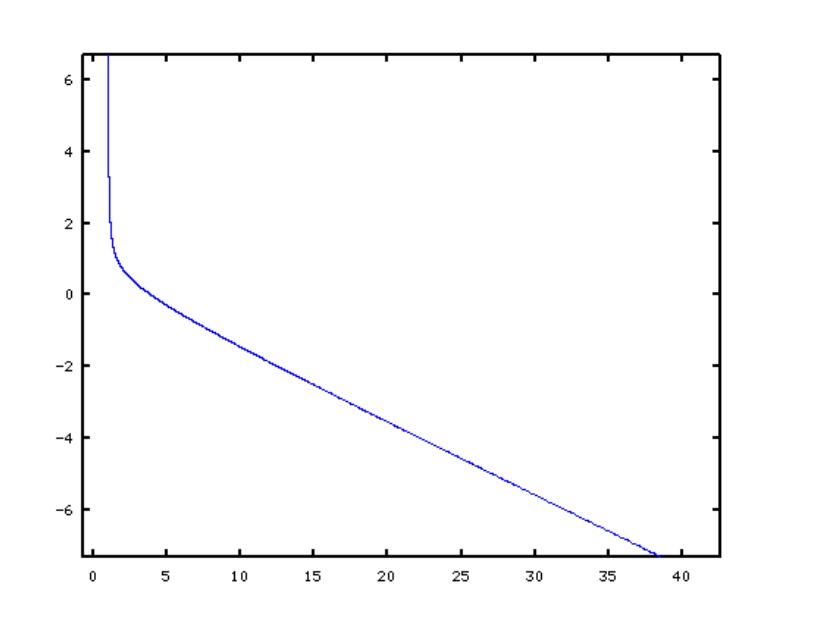
可见,在区间$(1,\\infty)$上,函数$h_i(\\gamma)$单调递减。假设$h_i(\\gamma)$的根为$\\gamma^*$,论文Numerical solution of a secular equation证明了,如果初始点选在$\\gamma^*$的左侧,则牛顿法必定收敛。换句话说,如果初始点$\\gamma$满足$h_i(\\gamma)>0$,则用牛顿法得到的$\\gamma$序列收敛到$\\gamma^*$
如何找这个初始点呢?论文Numerical solution of a secular equation构造了$h_i(\\gamma)$的一个下界函数$g_i(\\gamma)\\le h_i(\\gamma)$,通过求解$g_i(\\gamma)=0$得到根$\\gamma$,则有$0=g_i(\\gamma)\\le h_i(\\gamma)$,从而求得初始点。
现在我们推出这个下界函数。先讨论i<n的情况,然后讨论i=n的情况。
我们直接通过函数$h_i(\\mu)$来推出下界函数。根据前面所述,
$h_i(\\mu)=1 + \\sum_{i=j}^n \\frac{z_j^2}{\\delta_j-\\mu}$
$=1 + \\sum_{j\\ne i}^n \\left(\\frac{z_j^2}{\\delta_j} + \\frac{z_j^2/\\delta_j^2}{1/\\mu - 1/\\delta_j} \\right) -\\frac{z_i^2}{\\mu}$
$=1 + \\sum_{j<i}^n \\left(\\frac{z_j^2}{\\delta_j} + \\frac{z_j^2/\\delta_j^2}{1/\\mu - 1/\\delta_j} \\right) + \\sum_{j>i+1}^n \\left(\\frac{z_j^2}{\\delta_j} + \\frac{z_j^2/\\delta_j^2}{1/\\mu - 1/\\delta_j} \\right) -\\frac{z_i^2}{\\mu} + \\frac{z_{i+1}^2}{\\delta_{i+1}} + \\frac{z_{i+1}^2/\\delta_{i+1}^2}{1/\\mu - 1/\\delta_{i+1}}$
当j<i时,$\\delta_j < 0$,因此$1/\\mu-1/\\delta_j>0$
当j>i时,$\\mu<\\delta_j$,同样有$1/\\mu-1/\\delta_j>0$
所以
$h_i(\\mu)\\ge 1+\\sum_{j\\ne i}\\frac{z_j^2}{\\delta_j} + \\frac{z_{i+1}^2/\\delta_{i+1}^2}{1/\\mu - 1/\\delta_{i+1}} - \\frac{z_i^2}{\\mu}$
这时,用$\\gamma=\\frac1{\\mu}$带入,得到
$h_i(\\gamma)\\ge 1+\\sum_{j\\ne i}\\frac{z_j^2}{\\delta_j} + \\frac{z_{i+1}^2/\\delta_{i+1}^2}{\\gamma - 1/\\delta_{i+1}} - z_i^2\\gamma$
令右边等于0,我们得到一个方程,通过通分,去分母,最后转成一个二次方程:
$z_i^2\\gamma^2 - \\left(1+\\frac{z_i^2}{\\delta_{i+1}} +\\sum_{j\\ne i}\\frac{z_j^2}{\\delta_j}\\right)\\gamma + \\left(1+\\sum_{j\\ne i}\\frac{z_j^2}{\\delta_j}\\right)/\\delta_{i+1} - \\frac{z_{i+1}^2}{\\delta_{i+1}^2}=0$
用求根公式可以得到两个解,注意定义域$\\gamma_i>\\frac1{\\delta_{i+1}}$,因此取大根即可。
当i=n时,此时的定义域为$\\gamma_n>0$,其实$h_n(\\gamma=0)=h_n(\\mu=\\infty)=1$也是有定义的,而且此时$\\gamma=0$是该函数的最左边的点,因此直接选取$\\gamma=0$作为初始点即可。
之后牛顿迭代:
$\\gamma(k+1)=-\\frac{h_i(\\gamma(k))}{h\'_i(\\gamma(k))}+\\gamma(k)$
一般两到三次迭代即可收敛,可以认为是O(1) 时间。
这里只讨论了分治算法最基本的实现,论文A Serial Implementation of Cuppen\'s Divide and Conquer Algorithm for the Symmetric Eigenvalue Problem还提到了用deflation加速,此外分治算法还有稳定性等问题。这里就不详细探讨了。
3. 参考文献
https://en.wikipedia.org/wiki/Divide-and-conquer_eigenvalue_algorithm
A. Melman Numerical solution of a secular equation
J Rutter A Serial Implementation of Cuppen\'s Divide and Conquer Algorithm for the Symmetric Eigenvalue Problem Chapter 3。本文的一些插图来自这篇文章。
本文属作者原创,转载请注明出处
http://www.cnblogs.com/qxred/p/dcalgorithm.html
本系列目录: