UVA 11475 后缀数组/KMP

Posted 2020-08-04 キリト

 

题目链接：

题意：给定一个只含字母的字符串，求在字符串末尾添加尽量少的字符使得字符串为回文串。

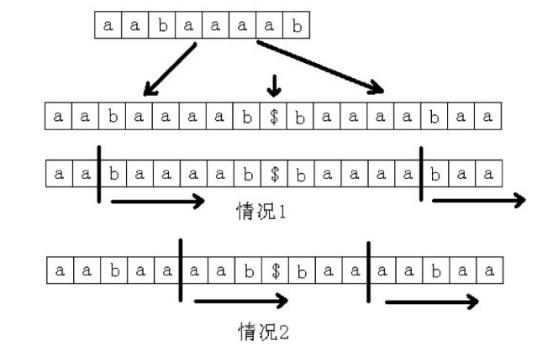
思路：因为只能从末尾添加字符，所以其实求的是最长的后缀回文串。那么添加的字符为除了这个原串的最长后缀回文串之外的其他字符。于是问题就转变成了求字符串的最长后缀回文串，对于后缀数组求回文串子串的做法，将整个字符串反过来写在原字符串后面，中间用一个特殊的字符隔开。这样就把问题变为了求这个新的字符串的某两个后缀的最长公共前缀。奇数长度和偶数长度的分开做。对于求奇数长度，假设现在枚举的位置为i,那么对应在反过来的串的位置为2*len-i。[len为输入字符串的长度,字符串的下标从0开始],求i和2*len-i的最长公共前缀，如果长度等于len-i那么就说话后缀i是回文后缀。 同理偶数长度的位置是i和2*len-i+1。关于求任意两个后缀的最长公共前缀可以用预处理+RMQ的做法。总的复杂度为O(nlogn)

 

#define _CRT_SECURE_NO_DEPRECATE
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<time.h>
#include<cmath>
#include<set>
using namespace std;
typedef long long int LL;
const int MAXN = 100000 * 2 + 10;
int wa[MAXN], wb[MAXN], wv[MAXN], WS[MAXN];
int cmp(int *r, int a, int b, int l)
{
    return r[a] == r[b] && r[a + l] == r[b + l];
}
void da(int *r, int *sa, int n, int m)
{
    int i, j, p, *x = wa, *y = wb, *t;
    for (i = 0; i < m; i++) WS[i] = 0;
    for (i = 0; i < n; i++) WS[x[i] = r[i]]++;
    for (i = 1; i < m; i++) WS[i] += WS[i - 1];
    for (i = n - 1; i >= 0; i--) sa[--WS[x[i]]] = i;
    for (j = 1, p = 1; p < n; j *= 2, m = p)
    {
        for (p = 0, i = n - j; i < n; i++) y[p++] = i;
        for (i = 0; i < n; i++) if (sa[i] >= j) y[p++] = sa[i] - j;
        for (i = 0; i < n; i++) wv[i] = x[y[i]];
        for (i = 0; i < m; i++) WS[i] = 0;
        for (i = 0; i < n; i++) WS[wv[i]]++;
        for (i = 1; i < m; i++) WS[i] += WS[i - 1];
        for (i = n - 1; i >= 0; i--) sa[--WS[wv[i]]] = y[i];
        for (t = x, x = y, y = t, p = 1, x[sa[0]] = 0, i = 1; i < n; i++)
            x[sa[i]] = cmp(y, sa[i - 1], sa[i], j) ? p - 1 : p++;
    }
    return;
}
int Rank[MAXN], height[MAXN], sa[MAXN];
void calheight(int *r, int *sa, int n){
    int i, j, k = 0;
    for (i = 0; i <= n; i++) { Rank[sa[i]] = i; }
    for (i = 0; i < n; height[Rank[i++]] = k){
        for (k ? k-- : 0, j = sa[Rank[i] - 1]; r[i + k] == r[j + k]; k++);
    }
    return;
}
int RMQ[MAXN], mm[MAXN], best[20][MAXN];
void initRMQ(int n){
    int i, j, a, b;
    for (mm[0] = -1, i = 1; i <= n; i++)
        mm[i] = ((i&(i - 1)) == 0) ? mm[i - 1] + 1 : mm[i - 1];
    for (i = 1; i <= n; i++) best[0][i] = i;
    for (i = 1; i <= mm[n]; i++)
        for (j = 1; j <= n + 1 - (1 << i); j++)
        {
        a = best[i - 1][j];
        b = best[i - 1][j + (1 << (i - 1))];
        if (RMQ[a]<RMQ[b]) best[i][j] = a;
        else best[i][j] = b;
        }
    return;
}
int askRMQ(int a, int b){
    int t;
    t = mm[b - a + 1]; b -= (1 << t) - 1;
    a = best[t][a]; b = best[t][b];
    return RMQ[a]<RMQ[b] ? a : b;
}
int lcp(int a, int b){
    int t;
    a = Rank[a]; b = Rank[b];
    if (a>b) { t = a; a = b; b = t; }
    return(height[askRMQ(a + 1, b)]);
}
char str[MAXN];
int r[MAXN], len, lenstr;
void solve(){
    int plr = 1;
    for (int i = 0; i < lenstr; i++){ //奇长度回文
        int idx = 2 * lenstr - i;
        if (idx<len&&lcp(i, idx) >= lenstr - i){
            plr = max(plr, (lenstr - i) * 2 - 1);
        }
    }
    for (int i = 0; i < lenstr; i++){ //偶长度回文
        int idx = 2 * lenstr - i + 1;
        if (idx<len&&lcp(i, idx) >= lenstr - i){
            plr = max(plr, (lenstr - i) * 2);
        }
    }
    printf("%s", str);
    for (int i = lenstr - 1 - plr; i >= 0; i--){
        printf("%c", str[i]);
    }
    printf("\\n");
}
int main(){
//#ifdef kirito
//    freopen("in.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
//#endif
    //    int start = clock();
    while (~scanf("%s", str)){
        lenstr = strlen(str); len = lenstr;
        for (int i = 0; i < lenstr; i++){
            r[i] = str[i];
        }
        r[len++] = 0;
        for (int i = lenstr - 1; i >= 0; i--){
            r[len++] = str[i];
        }
        r[len] = 1;
        da(r, sa, len + 1, 128);
        calheight(r, sa, len);
        for (int i = 1; i <= len; i++){ RMQ[i] = height[i]; }
        initRMQ(len);
        solve();
    }
    //#ifdef LOCAL_TIME
    //    cout << "[Finished in " << clock() - start << " ms]" << endl;
    //#endif
    return 0;
}

思路二：本题也可以用KMP的做法，由于只能在末尾添加字符所以可以用反过来的串和原串进行匹配，看看最后能匹配多次就是最长后缀回文的长度了。对于求回文串不仅仅可以用后缀数组和KMP，HASH，manacher,回文树都是可行的办法，不过这题还是KMP比较容易写而且运行时间明显比后缀数组快

#define _CRT_SECURE_NO_DEPRECATE
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<time.h>
#include<cmath>
#include<set>
using namespace std;
typedef long long int LL;
const int MAXN = 100000 * 2 + 10;
char str[MAXN], restr[MAXN];
int Next[MAXN], len;
void getNext(char *s, int len){
    int i = 0, j = -1;
    memset(Next, 0, sizeof(Next));
    Next[0] = -1;
    while (i<len){
        if (j == -1 || s[i] == s[j]){
            i++; j++;
            Next[i] = j;
        }
        else{
            j = Next[j];
        }
    }
}
int KMP(char *str, char *restr, int len){
    int j = 0;
    for (int i = 0; i<len; i++){
        while (j != -1 && restr[j] != str[i]){
            j = Next[j];
        }
        if (restr[j] == str[i]){
            j++;
        }
        if (j == -1){
            j = 0;
        }
    }
    return j;
}
int main(){
//#ifdef kirito
//    freopen("in.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
//#endif
//    int start = clock();
    while (scanf("%s", str) != EOF){
        len = strlen(str);
        for (int i = len - 1; i >= 0; i--){
            restr[len - i - 1] = str[i];
        }
        getNext(restr, len);
        printf("%s", str);
        for (int i = KMP(str, restr, len) ; i<len; i++){
            printf("%c", restr[i]);
        }
        printf("\\n");
    }
//#ifdef LOCAL_TIME
//    cout << "[Finished in " << clock() - start << " ms]" << endl;
//#endif
    return 0;
}