数据结构（下）

Posted 2022-09-22 poweryao

1.树套树

(1)树状数组套树状数组

前置：

树状数组如何支持区间加以及区间查询

维护一个差分数组，用来求一个位置的值，我们只需要把前缀和看作是一个矩形，

减去两数插值产生的贡献即可

1.P4514 上帝造题的七分钟

题意：支持矩形加某个数和矩形查询值。

考虑将每个点差分，当我们要将\((a,b),(x,y)\)范围内的矩阵加1时，其实就是：

\(A(a,b)+1\)

\(A(x,b+1)-1\)

\(A(a,y+1)-1\)

\(A(x+1,y+1)+1\)

于是乎，前缀和：

\[\sum_i=a^x\sum_j=b^yA(i,j)*(x-i+1)*(y-j+1)\]

\[\sum_i=a^x\sum_j=b^yA(i,j)*(x*y+1)+A(i,j)*i*j-A(i,j)*i*(y+1)-A(i,j)*j*(x+1)\]

维护\(A(i,j)*i*j,A(i,j)*i,A(i,j)*j,A(i,j)\)即可

(2).权值线段树套区间线段树

1.P3332 [ZJOI2013]K大数查询

题意：

1 a b c：表示在第a个位置到第b个位置，每个位置加上一个数c

2 a b c：表示询问从第a个位置到第b个位置，第C大的数是多少

直接上。。。

(3).树状数组套主席树

我们发现单个的主席树就类似于我们单个的一个前缀和。当我们需对一个点进行修

改，并且求值是，我们考虑用树状数组维护区间关系，使每一次的修改次数下降到

\(O(log^2n)\),但每次查询也变成了这样的复杂度。

1.P2617 Dynamic Rankings 裸题

2.动态逆序对

3.P4175 [CTSC2008]网络管理

题意：在一棵树上维护一条链上的第k大的值，并支持修改。

题解：直接树套树再套一个树剖，优秀\(O(nlog^3n)\)

(4).线段树套平衡树

1.P3380 【模板】二逼平衡树（树套树）

某巨巨说并没有什么用，这个的话我其实使自己\(yy\)出来的\(O(log^3n)\)的做法，

但蒟蒻自带大常数，就是过不了。

2.点分治

点分治的复杂度正确在于每一次都求了一边重心，维护了树的高度，总复杂度是

\(O(nlog n)\)的

1.P3806 【模板】点分治1

题解：板子滚粗

2.P4149 [IOI2011]Race

题解：多维护一个边的数量

3.P2634 [国家集训队]聪聪可可

题解：板子滚粗

3.动态点分治

动态点分治就是支持修改对吧。。。。。。

然后我们知道本来点分治就是不断的找重心，于是根据此我们可以建出一棵点分

树，非常的优秀。而我们知道其实每次点分治无非就是每次重心的答案总和。我

们直接记录每个重心的答案即可。建出来的点分树复杂度还是非常有保障的。

动态点分治还是很给人启示的。

1.P3345 [ZJOI2015]幻想乡战略游戏

题意：一棵树上，有边权，点权。支持点权修改，要求找出一个点，使所有点的

权值*到这个点的距离和最小。

题解：

1.这道题的优美性质就是要找到这棵树的重心。

2.这道题如果直接找重心满足$2\times sumd_v>sumd_u $则向v走。

3.我们要统计的是所有重心到这个点的距离*权值。点分树可以做到。类似于：

ll count(int x)
    ll res = 0 ;
    res += sumval[x] ;
    for(int i = x ; Hfa[i] ; i = Hfa[i] )
        ll fr = Distance( x , Hfa[i] ) ;
        res += ( sumval[Hfa[i]] - sumf[i] ) ;
        res += 1ll * ( sumg[Hfa[i]] - sumg[i] ) * fr ;
    
    return res ;

ll query(int x)
    ll tmp = count( x ) ;
    for(int i = Fire[x] ; i ; i = Nex[i] )
        int v = To[i] ;
        if( count( v ) < tmp ) return query( near[i] ) ;
    
    return tmp ;

2.P3241 [HNOI2015]开店

这道题其实和上面的套路一样，点分树建一波，vector记一波。

3.P3676 小清新数据结构题

就是一道神题。

我们用\(S_i\)表示\(i\)的子树

这里你会发现\(\sum_i=1^nS_i^2\)是个不太好处理而且没有什么非常优美的性质

我们暂时先不考虑修改，让我们看一下换根回产生什么样的影响：

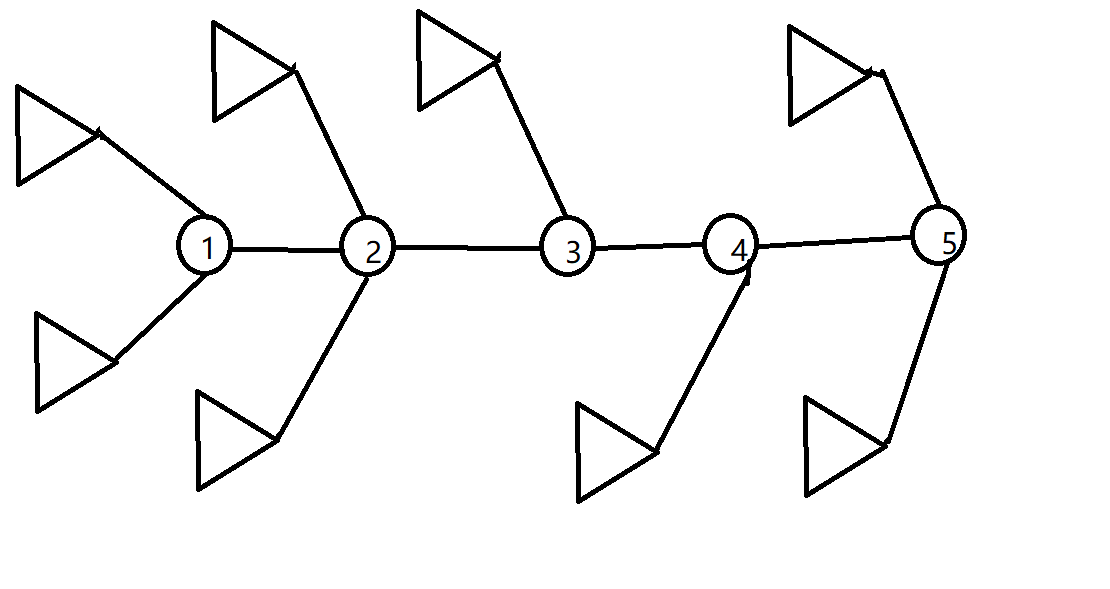
假如这棵树是这样的。现在以\(5\)号点为根，现在打算以\(1\)号点为根

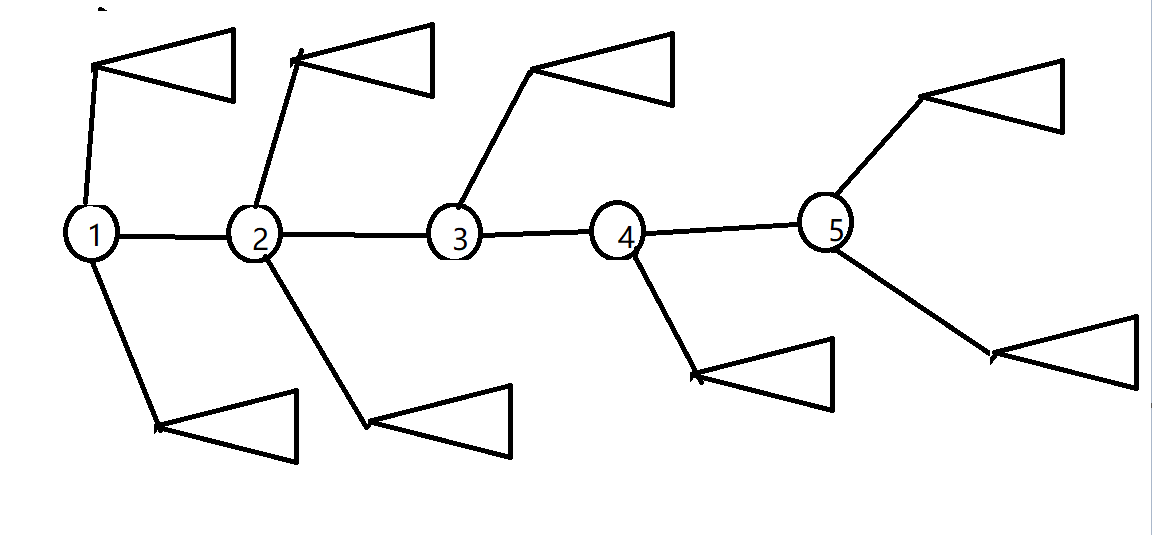
发现只有路径\(1-5\)的点上的子树大小会变。于是你会发现一个优美而又可怕的结

论：

\[\sum_i=1^nS_i(Sum-S_i)\]

是个定值。设这个定值为\(W\)

那么答案就是

\[ans=Sum\sum_i=1^nS_i-W\]

然而

\[\sum_i=1^nS_i=\sum_i=1dep_ivali\]

这个点分树可以直接胜任

我们开始考虑单点的修改。

对于任何两个点，他们的乘积所产生的贡献既为他们刚好没被分在同一子树内。

这样的情况就有\(dis(i,j)\)次

所以

\[\sum_i=1^nS_i(Sum-Si)=\sum_i=1^n\sum_j=1^ndis(i,j)val_ival_j\]

对于单点修改：

\[W_new=add*\sum_j=1^ndis(i,j)*val_j\]

这个的话，点分树还是可以胜任

写法和上面的大同小异

4.捉迷藏 P2056 [ZJOI2007]捉迷藏

不是我说难码，可以学习的就是那个堆的使用

struct node
    priority_queue<int> A , B ;
    void insert(int x)
        A.push(x) ;
    
    void dele(int x)
        if( A.top() == x ) A.pop() ;
        else B.push(x) ;
    
    int Top()
        while( !A.empty() && !B.empty() && A.top() == B.top() ) A.pop() , B.pop() ;
        if( A.empty() ) return -inf ;
        else return A.top() ;
    
    int nex_top()
        int rt = Top() ;
        if( rt == -inf ) return -inf ;
        A.pop() ; int nexrt = Top() ;
        A.push( rt ) ;
        return nexrt ;
    
ans , tofa[N] , stree[N] ;

4.LCT

(1)链信息：

1.P1501 [国家集训队]Tree II

2.P2147 [SDOI2008]洞穴勘测

3.P3690 【模板】Link Cut Tree （动态树）

4.P4332 [SHOI2014]三叉神经树

被神仙叫做模板题。每棵平衡树在其中维护最深不是2的以及最深不是1的点。然

后乱搞就行。

(2)维护图连通性：

1.P2387 [NOI2014]魔法森林

排个序，维护一波。

2.P2542 [AHOI2005]航线规划

维护双连通，倒叙做

3.P4234 最小差值生成树

这里的话需要先新建节点，表示两点之间的边权。维护链的最小值，删掉就行。

4.P4172 [WC2006]水管局长

不知道为什么别人一个个跑得飞快。这道题，也就是维护一个最大边，形成一个

圈就删去即可。

(3)维护子树信息：

1.P4219 [BJOI2014]大融合

注意虚子树修改在\(link\)和\(access\)中要进行。

2.P3703 [SDOI2017]树点涂色

在浑浊的\(LCT\)中，这简直就是一股清流。

线段树\(dfs\)序来维护一棵子树的颜色总和。

每次将根到某个点的链全部染成同一种颜色就是一次\(access\)操作。于是乎

\(access\)每断一次边下面的原来链的子树答案加1，新加入的链的子树答案全部减

1

5.树链剖分

这是一个收集篇，收集树剖好题。

1.P4211 [LNOI2014]LCA

建个下标为标号的主席树的dfs序（维护区间差分个数）

6.扫描线

1.P1972 [SDOI2009]HH的项链

感受一下

2.P4113 [HEOI2012]采花

感受一下

3.P1856 [USACO5.5]矩形周长Picture

luogu无矩形面积并，不过这个也差不多。

跑两边扫描线，每次加差值就行。

4.P1502 窗口的星星