并查集

Posted 2020-07-29 --Allen--

一、引例

给定 N 个对象，以及若干条连接这些对象的边。求连通分量的个数，或者判断任意两个对象是否连通。如图1，有2个连通分量。

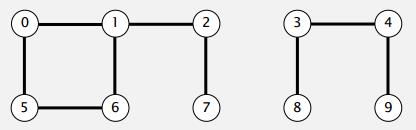
图1 10个顶点及7条边

这个问题乍一看似乎遥不可及，但是如果掌握了并查集，能够轻松解决。

二、思路

为了方便描述对象，把对象抽象成数字。如果有 N 个对象，那就用数字 0 到 N-1 来表示不同对象。
假定现在有三条命令：

union(p, q)：表示连接 p 和 q.
connected(p, q)：判断 p 和 q 是否连通。
count()：返回连通分量的个数。

给定10个对象，假设这些对象用数字0-9表示，当我们做了如下操作后：

union(4, 3)
union(3, 8)
union(6, 5)
union(9, 4)
union(2, 1)
union(5, 0)
union(7, 2)
union(6, 1)
union(1, 0)

将会形成图1的样子。这时候如果执行 connected(0, 7)，命令应该回答 yes. 如果执行 connected(7， 8)，命令应该回答 no.

根据以上描述，抽象出一个 class，命名为 UF。定义如下。

class UF{
    UF(int N);
    void uni(int p, int q);//C++ 中 union 是关键字，这里避免报错使用 uni 替代。
    bool connected(int p, int q);
    int root(int i);
    int count();
}

接下来要做的事情就是，如何实现这个类？
咱们先不管这些事情，不如，先把客户端测试程序写好。这个客户端测试程序的意思是从标准输入先读入一个整数，表示一共有多少对象。然后读入对象与对象之间的边。数据格式大概是这样子的:

10
2 3
6 7
1 9
…

第一行表示一共有10个对象，第二行表示2和3是连通的，第三行表示6和7是连通的，后面以此类推。

int main()
{
    int N;
    int p, q;
    while (cin >> N)
    {
        UF uf(N);
        while (cin >> p >> q)
        {           
            uf.uni(p, q);
            cout << p << " " << q << endl;
        }
        cout << uf.count() << " components!" << endl;
    }
    return 0;
}

三、实现

用数字表示对象有个好处，那就是数字可以当作数组的索引。假如有一个数组 id[]，它的长度就是对象的个数。现在有个想法，如果两个对象是连通的，就认为它们是同一组，既然是同一组，可以为它们分配一个 id 号，为了方便，可以任意指定同一组中的任意一个对象作为该组的 id 号。

图2 利用 id 数组将对象划分到不同的组。

如图2，对象0、5、6被划分到了第 0 组，对象1、2、7 被划分到了第1组，剩余的都被划分到了第 8 组。
在刚开始的时候，所有的对象自成一组，也就是让 id[i] = i. 这样，有 N 个对象，有 N 个组。构造函数可以这样来写。

UF(int n):id(n){
    for(int i = 0; i < n; ++i) id[i] = i;
}

那么，很直观的 union 操作应当就是给两个对象分配相同的 id 号。下面是一种实现方式。

void uni(p, q){
    // 如果 p 和 q 不同组，我们让 p 中的所有对象的组号和 q 的组号相同
    int pid = id[p];
    int qid = id[q];
    if(pid != qid){
        for(int i = 0; i < n; ++i){
            if(id[i] == pid) id[i] = qid;
        }
    }
}

不得不说的是，当面对大量样本时，这种做法是相当的慢。因为每次 union 你都要把 id 数组遍历一次。那么换个思路，我们在 id 数组中存放父对象索引，这样，只要是同一个对象生出的后代，必然都可以通过这种关系维系。因为，只要两个对象有公共祖先，那它们一定在同一组。简单的说，可以通过id[id[…id[i]…]]来找到根节点。而根节点父亲就是它自己，也就是说 id[r] = r。

图3 在 id 数组中存储父对象的索引



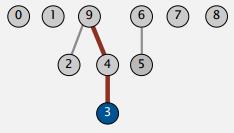
图4 图3中的id数组转换成的树结构。

既然如此，如果要union两个对象，只要找到两个对象的根节点，然后让其中一个根节点成为另一个根节点的父亲就行了。代码改成这样。

void uni(int p, int q){
    int i = root(p);
    int j = root(q);
    if (i != j){
        id[i] = j;
    }
}

int root(int i){
    while(i != id[i]){
        i = id[i];
    }
    return i;
}

看起来似乎都完成了，那 connected 的实现就很容易了，只要两个节点有相同的根节点，就可以很容易判定它们是连通的。

bool connected(int p, int q){
    return root(p) == root(q);
}

到此为止，还剩下最后一个任务，就是求连通分量的个数。在刚初始化的时候，连通分量的个数等于对象的个数，因为对象刚开始的时候都是不相连的。每当做union操作的时候，如果两个对象不在同一个组，必然会导致连通分量减少1个。所以，用一个counter计数器来记录连通分量的个数就行了。在初始化的时候，counter初始化为对象的个数。然后在union操作里加一句话就行了。

void uni(int p, int q){
    int i = root(p);
    int j = root(q);
    if (i != j){
        id[i] = j;
        --counter;//每次union的时候，连通分量的个数都会少一个。
    }
}
int count(){
    return counter;//直接返回计数器即可
}

至此为止，上面的算法基本能够满足日常需求。但是还存在改进的地方。

四、改进

在union中，只是简单粗暴的让其中一个根节点成为另一个根节点的父亲。然而，可能会出现这样的情况：

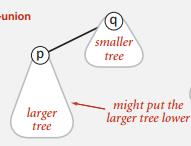
图5 大树成为了小树的子树，导致树的重量上的不平衡。

如果有一种办法，能够识别出大树和小树，可以有选择的让大树成为小树的父亲，这样可以有效减少树的深度。
这里的大树，指的是树中的节点比较多，不是指树的深度大。


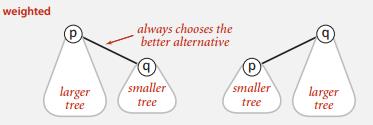
图6 让大树成为小树的父亲

解决这个问题的办法是，增加一个长度为N(对象的个数)数组sz[]，来记录树的重量（即树中节点的个数）。
在初始化的时候，sz中的每个元素都初始化成1。union操作改成这样。

void uni(int p, int q){
    int i = root(p);
    int j = root(q);
    if (i != j){
        // 有选择性的让小树成为大树的子树。
        if (sz[i] < sz[j]) {
            id[i] = j;
            sz[j] += sz[i];
        }
        else{
            id[j] = i;
            sz[i] += sz[j];
        }
        --counter;//每次union的时候，连通分量的个数都会少一个。
    }
}

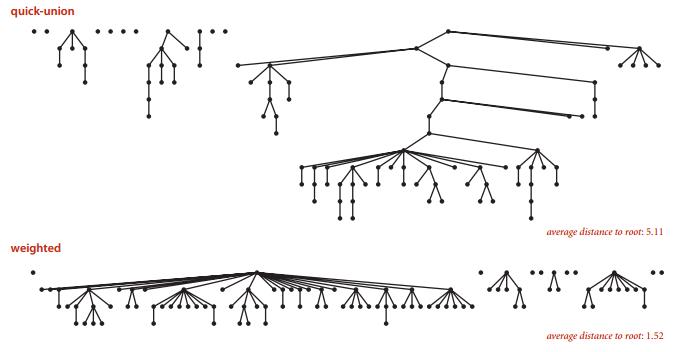
图7 改进前后的对比

五、就这样结束了吗？

先来看这样一张图。

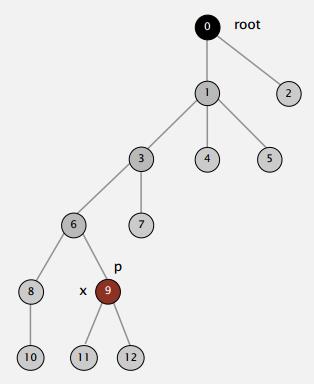
图8 经过若干次union后形成的树

如果能把图8中的树的高度再压缩压缩，是不是更好？就像下面这样，当需要查询对象9的根节点的时候，查询完成后，顺便把对象9的父亲改为根节点.


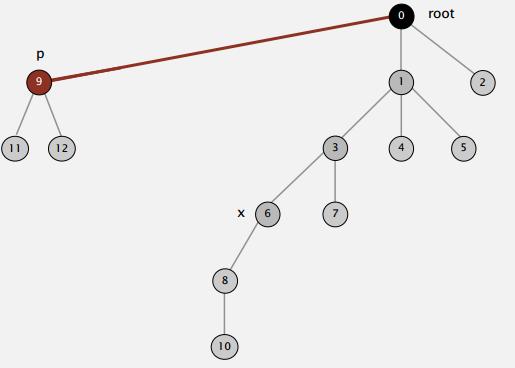
图9 将对象9的父亲改为根节点

当需要查询对象6的根节点时，查询完成后，顺便把6的父改为根节点。



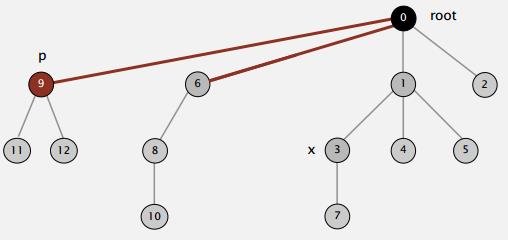
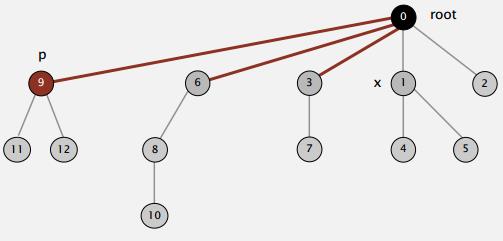
图10 压缩树的高度

上面的这个过程称之为

路径压缩

。听起来很高大上，实现起来相当简单。不过也可以按照另外的方式来实现，比较每次将路径压缩为原来的一半，这样的话，只要有root中加一行就可以解决。

int root(int i){
    while(i != id[i]){
        id[i] = id[id[i]];//实现路径压缩
        i = id[i];
    }
    return i;
}

六、完整的代码

#include <iostream>
#include <vector>
using namespace std;

class UF
{
public:
    UF(int n) :id(n), sz(n, 1), counter(n)
    {
        for (int i = 0; i < n; ++i) id[i] = i;
    }

    void uni(int p, int q)
    {
        int i = root(p);
        int j = root(q);
        if (i != j)
        {
            //有选择的让小树成为大树的子树。
            if (sz[i] < sz[j]) {
                id[i] = j;
                sz[j] += sz[i];
            }
            else{
                id[j] = i;
                sz[i] += sz[j];
            }
            --counter;
        }
    }

    int root(int i)
    {
        while (i != id[i])
        {
            //路径压缩
            id[i] = id[id[i]];
            i = id[i];
        }
        return i;
    }

    bool connected(int p, int q)
    {
        return root(p) == root(q);
    }

    int count(){
        return counter;
    }
private:
    int counter;
    vector<int> id;
    vector<int> sz;
};

int main()
{
    int N;
    int p, q;
    while (cin >> N)
    {
        UF uf(N);
        while (cin >> p >> q)
        {           
            uf.uni(p, q);
            cout << p << " " << q << endl;
        }
        cout << uf.count() << " components!" << endl;
    }
    return 0;
}

七、并查集的应用

我就不讲什么用于游戏啊、连通性检测啊、Fortran语言等价性语句检测啊什么的了，直接上个题目比较实际。
leetcode 第200题

题目：Given a 2d grid map of ‘1’s (land) and ‘0’s (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
翻译：给你一个网格图，每个格点记录的不是‘1’(表示土地)就是‘0’(表示海洋), 现在你要计算岛屿的个数。一座岛屿应该被海洋包围，岛屿由水平和垂直方向的土地形成。对于网格图的4条边，你假定它被海洋包围。

Example 1:

11110
11010
11000
00000

Answer: 1

Example 2:

11000
11000
00100
00011

Answer: 3
题目大意就是让你求连通分量的个数。
思路：利用并查集求连通分量。这里需要注意的是:

1. 只计算网格点中为‘1’的情况;
2. 在做连通时，只考虑当前节点的右边和下边的对象，上边和左边的不用考虑；
3. 节点的编号就是从左往右从上往下第几个位置，即 $\\color{#c7254e}{id=i\\times cols + j}$，注意不要把 $\\color{#c7254e}{cols}$ 写成了 $\\color{#c7254e}{rows}$.

答案：

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int rows = grid.size();
        if(rows == 0) return 0;
        int cols = grid[0].size();
        if(cols == 0) return 0;
        int n = rows * cols;
        int zeros = 0;
        UF uf(n);
        for(int i = 0; i < rows; ++i){
            for(int j = 0; j < cols; ++j){
                if(grid[i][j] == '1'){
                    int id = i*cols + j;
                    if(i+1<=rows-1 && grid[i+1][j] == '1'){
                        uf.uni(id, id + cols);
                    }
                    if(j+1<=cols-1 && grid[i][j+1] == '1'){
                        uf.uni(id, id + 1);
                    }
                }
                else
                {
                    ++zeros;
                }
            }
        }
        return uf.count() - zeros;
    }
};