计蒜客 Flashing Fluorescents(状压DP)
Posted taozi1115402474
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了计蒜客 Flashing Fluorescents(状压DP)相关的知识,希望对你有一定的参考价值。
You have nn lights, each with its own button, in a line. Pressing a light’s button will toggle that light’s state; if the light is on, it will turn off, and if the light is off, it will turn on. The lights change at 1 second timesteps. You can press a button at any time, but it will not take effect until the next timestep. Before each timestep, you may choose to push at most one button (you may also choose to not press any button).
Pushing a button will affect not just the light in question, but all lights down the line. More specifically, if you choose to press the i^th button right before the k^th timestep, then the (i + m)^th light will toggle on the (k + m)^th timestep (with i + m≤n). For example, if you press button 5 just before time 19, then light 5 will toggle at time 19, light 6 will toggle at time 20, light 7 will toggle at time 21, and so on. If you push a button that will take effect at the same time as its light would have toggled due to an earlier button press, then the two cancel each other out, including subsequent toggles.
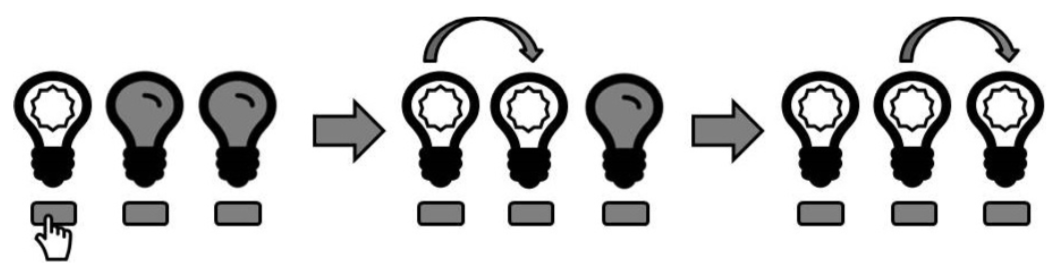
Suppose there are three lights, all of which are off at the start. If you press the first button before the first timestep, this will happen in three timesteps:
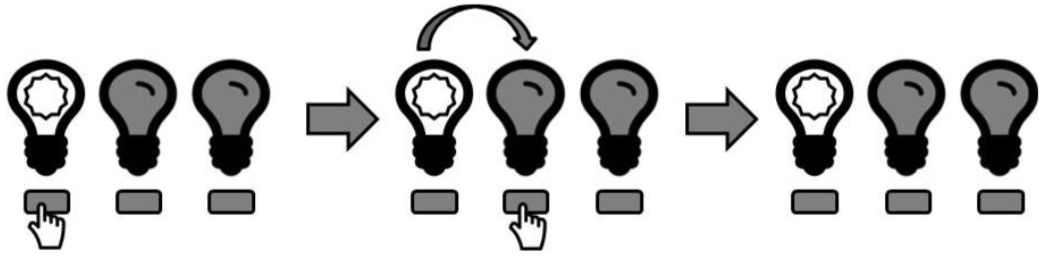
Now, suppose you press the first button before the first timestep, and then the second button between the first and second timesteps. The button press will cancel out the propagation, and this will happen (note that the propagation will go no further):
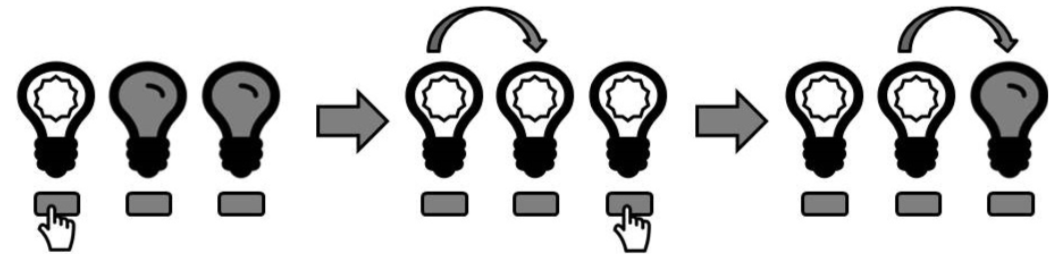
Now, suppose you press the first button before the first timestep, and then the third button between the first and second timesteps. All three lights will be on at the second timestep (but not the third):
You wish to turn on all the lights. What is the earliest time you could possibly see all of the lights turned on? Note that if the lights are all on at time t but not at time t + 1 due to this propagation, t is still the correct answer.
Input Format
Each input will consist of a single test case.
Note that your program may be run multiple times on different inputs.
Each test case will consist of a single string S(1≤∣S∣≤16). The string SS will contain only the characters 1 and 0, where 1 represents that that light is initially on, and 0 represents that that light is initially off. The first character is light 1, the next is light 2, and so on.
Output Format
Output a single integer, which is the earliest time at which all of the lights are on.
样例输入1
1101
样例输出1
1
样例输入2
1
样例输出2
0
样例输入3
000
样例输出3
2
题意
给你一个01串,1表示亮0表示灭,每分钟可以让一盏灯亮,但下一分钟后一盏灯会改变,下下一分钟后后一盏灯会改变,直到N。问你最少几分钟可以让所有灯亮。
题解
答案ans<=n,要构造全1,那么就是给你若干个01字符串,问你异或和为全1,显然是一定能构造出来的。
f[ans][S]代表第ans分钟是否有子集S。
代码
1 #include<bits/stdc++.h> 2 using namespace std; 3 4 bool f[20][1<<16]; 5 char a[20]; 6 int main() 7 8 while(scanf("%s",a)!=EOF) 9 10 int n=strlen(a),i,j,now=0,S=0; 11 memset(f,0,sizeof f); 12 for(int i=0;i<n;i++)if(a[i]==‘0‘)S|=1<<i; 13 f[0][S]=1; 14 while(!f[now][0]) 15 16 for(int S=0;S<1<<n;S++)f[now+1][S]=f[now][S]; 17 for(int i=0;i<n;i++) 18 19 int mask=0; 20 for(int j=0;j<now+1&&i+j<n;j++)mask|=1<<(i+j); 21 for(int S=0;S<1<<n;S++)if(f[now][S])f[now+1][S^mask]=1; 22 23 now++; 24 25 printf("%d\n",now); 26 27 return 0; 28
以上是关于计蒜客 Flashing Fluorescents(状压DP)的主要内容,如果未能解决你的问题,请参考以下文章