HDU - 1542 Atlantis[线段树+扫描线]

Posted 2020-11-10 极简主义

题目描述

HDU - 1542

求矩阵面积并。

好久没写题解了。。。哎，这道题折腾了我好几天。。。

不知道为什么zcydalao讲的方法不太好使，我AC不了，可能是我菜吧。。。于是用了某本蓝书的方法，这种方法明显更加简单粗暴。

解析：

线段树+扫描线经典题。

遇到这种求矩形面积并或者某些平面轮廓的问题时，我们通常有一种一般方法——扫描线。

具体而言，就是先任意选一条坐标轴，用一根平行于它的扫描线扫描这些矩形。

为了方便计算，我们可以首先将平行于扫描线的矩形的边拿出来，这样处理之后的图形就变成了一堆平行于坐标轴的线段，注意，这些线段分为矩形的上边界和下边界，务必严格区分。接下来为了便于扫描，我们将这些线段离散化。

以平行于(x)轴的扫描线为例，我们就将所有线段按照(x)坐标为依据进行离散化，并建立一个hash数组形成映射。

接下来就是用一颗线段树以离散化后为标准，一个单位一个单位地扫描这些线段，为了方便理解，我从zcy的ppt里偷几张图，而且其实他也是偷的图。至于为什么用线段树，当然你也可以用平衡树啊（逃。

首先离散化(x)坐标后，我们得到形如下面这张图的图形。当然经过预处理，我们只剩下一堆线段，所以你可以无视平行于(y)轴的那些线条。

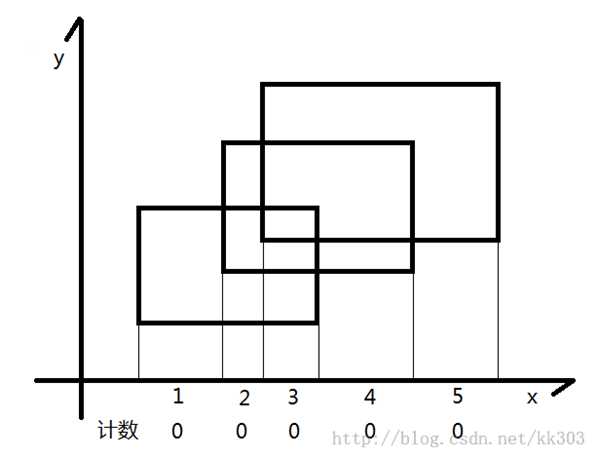
然后用一根扫描线去扫描，一旦遇到下边界，就让线段树在下边界所在这一区间的权值+1（图不太一样，我删了），表示这段区间被某个矩形覆盖了一次。一旦遇到上边界，就让线段树在上边界所在这一区间的权值+1。

比如说上面这个图，扫描线扫到最下面那个矩形的下边界时，([1,3])这个区间的权值就会+1。

这就是线段覆盖的一个概念，是有板子的，有兴趣的可以去百度一下。

注意，由于我们的线段树统计的是区间，所以在计hash值时需要特别注意。

那么我们怎么计算矩阵面积并呢？很简单，我们发现扫描线会把所有矩形分割成规则的小矩形，像这样：

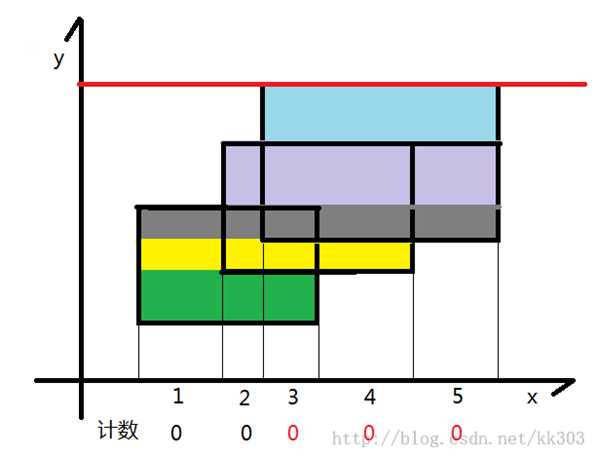
所以，对于每个小矩形，我们可以轻松地（个鬼，我就是这里搞不定才换方法）使用hash把小矩形的宽求出来，而高就是我们处理过后的两条线段之间的距离。那么，显而易见小矩形的面积就是高×宽，可以求出了。

具体来说，求宽就是hash出一条线段原来的左右端点(x)坐标，做差就得了。

线段树五问（摘自zcy dalao的ppt）：

1. Q：每个区间上需要计哪些值？

   A：一段区间被覆盖的次数cnt；当前合法的线段长度（当前扫描线位置扫出来的所有合法的矩形边界总长度）dat，也就是上面提到的小矩形的宽。

2. Q：需要什么标记？

   A：不需要标记。

3. Q：标记如何叠加？

   A：不需要标记。

4. Q：标记怎么下放？

   A：不需要。

5. Q：如何合并区间？

   A：比较恶心，也是难点。如果当前区间全部被覆盖的话，那么显然我们可以直接把dat给hash出来，而如果当前区间没有被完全覆盖，那么显然当前区间的合法线段总长dat就是由它的两个子区间加和而来，值得注意的时，我们要考虑它是不是叶子节点，如果一段区间是叶子节点，而且它还未被覆盖的话，那它的dat显然为0，否则它被覆盖的话，dat就是1。

有一个小细节，就是pushup，在递归的最后一层必须写上，因为某一区间可能被多条线段同时覆盖，如果去掉长的那一条，却不代表剩下的短的线段也去掉了，剩下的我们也要计入。所以在递归到最后一层节点时，我们还要考虑它的子区间是否有覆盖线段，这个虽然不难想到，但我也是yy出来的（逃。

参考代码：

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#define N 210
#define INF 0x3f3f3f3f
using namespace std;
double ans,hah[N<<1];
int cnt;
struct ret{
    double x1,x2,y;
    int st;
}h[N<<1];
struct seg{
    int l,r;
    int cnt;
    double dat;
}t[N<<2];
bool cmp(ret a,ret b){return a.y<b.y;}
void pushup(int p)
{
    if(t[p].cnt) t[p].dat=hah[t[p].r+1]-hah[t[p].l];//如解析所示
    else if(t[p].l==t[p].r) t[p].dat=0;
    else t[p].dat=t[p<<1].dat+t[p<<1|1].dat;
}
inline void build(int p,int l,int r)
{
    t[p].l=l,t[p].r=r;
    t[p].cnt=t[p].dat=0;
    if(l==r) return;
    int mid=(l+r)>>1;
    build(p<<1,l,mid);
    build(p<<1|1,mid+1,r);
}
inline void change(int p,int l,int r,int val)
{
    if(l<=t[p].l&&t[p].r<=r){
        t[p].cnt+=val;
        pushup(p);//这里的pushup不能漏，这个pushup保证递归到最后的那个区间也被其子区间更新 
        return;
    }
    int mid=(t[p].l+t[p].r)>>1;
    if(l<=mid) change(p<<1,l,r,val);
    if(r>mid) change(p<<1|1,l,r,val);
    pushup(p);
}
int main()
{
    int n;
    int k=0;
    while(cin>>n&&n!=0)
    {
        ans=0;cnt=0;
        int tt=0;
        memset(hah,0,sizeof(hah));
        memset(h,0,sizeof(h));
        double x1,x2,y1,y2;
        for(int i=1;i<=n;++i){
            scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
            //别被这个离散化吓到，其实很简单的
            h[++cnt].y=y1;
            h[cnt].x1=x1;
            h[cnt].x2=x2;
            h[cnt].st=1;
            h[++cnt].y=y2;
            h[cnt].x1=x1;
            h[cnt].x2=x2;
            h[cnt].st=-1;
            hah[++tt]=x1;
            hah[++tt]=x2;   
        }
        sort(h+1,h+cnt+1,cmp);
        sort(hah+1,hah+tt+1);
        unique(hah+1,hah+tt+1);
        build(1,1,cnt);
        for(int i=1;i<=cnt;++i){
            int x,y;
            x=lower_bound(hah+1,hah+tt+1,h[i].x1)-hah;
            y=lower_bound(hah+1,hah+tt+1,h[i].x2)-hah-1;
            ans+=t[1].dat*(h[i].y-h[i-1].y);
            change(1,x,y,h[i].st);
        }
        printf("Test case #%d
Total explored area: %.2lf

",++k,ans);
    } 
    return 0; 
}