线段树入门之惊鸿一瞥

Posted 2022-05-10 dragondragon

--------------------------走吧，目标伟大航路！

线段树的点点滴滴：

先从一些直观性的角度来看：

 

 

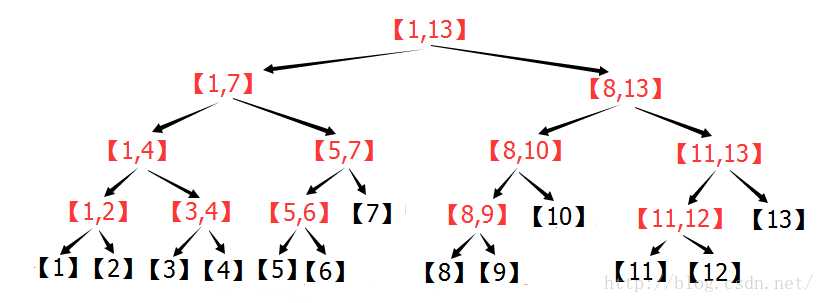
上图是用二分法丫！问题来喽，

对于给定区间[2,12]要如何分解成上述区间呢,何以分解之？

分解方法一：自下而上合并——利于理解

先考虑树的最下层，将所有在区间[2,12]内的点选中，然后，若相邻的点的直接父节点是同一个，

那么就用这个父节点代替这两个节点（父节点在上一层）。这样操作之后，本层最多剩下两个节点。

若最左侧被选中的节点是它父节点的右子树，那么这个节点会被剩下。若最右侧被选中的节点是它的父节点的左子树，那么这个节点会被剩下。

中间的所有节点都被父节点取代。对最下层处理完之后，考虑它的上一层，继续进行同样的处理。

继续沿用上面的那个引子图丫：

这是n=13的线段树，区间[2,12]，按照上面的叙述进行操作的过程图：

 

 

 

 

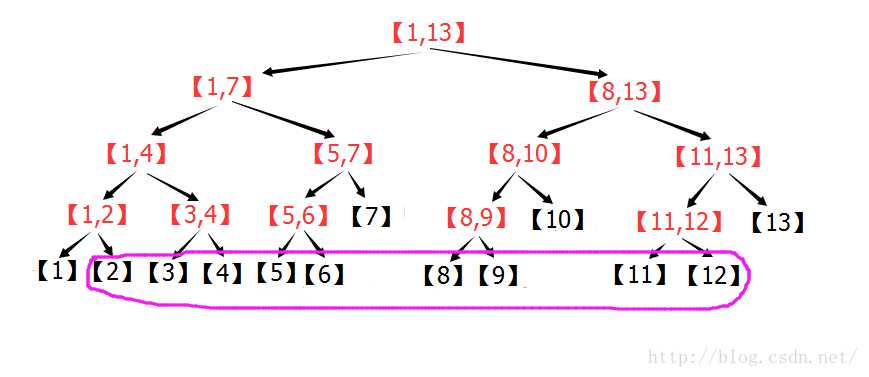
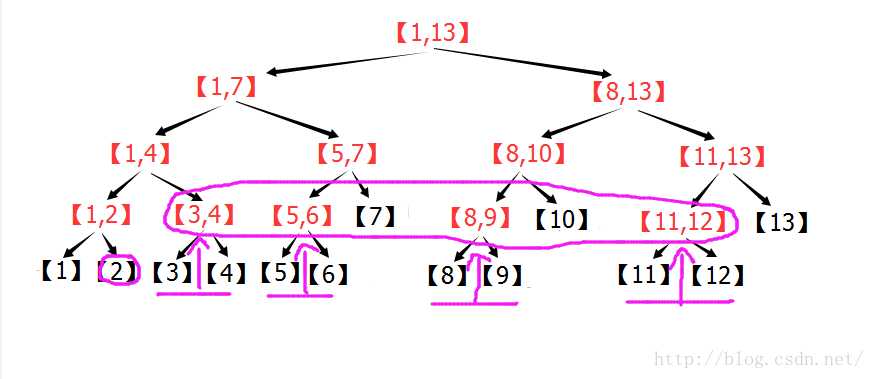
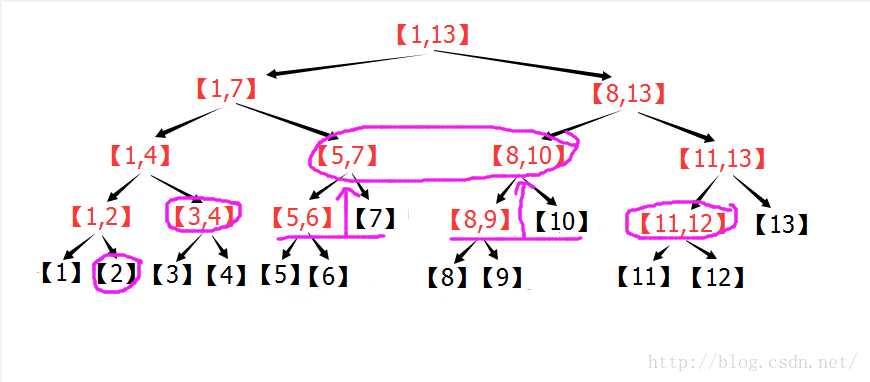
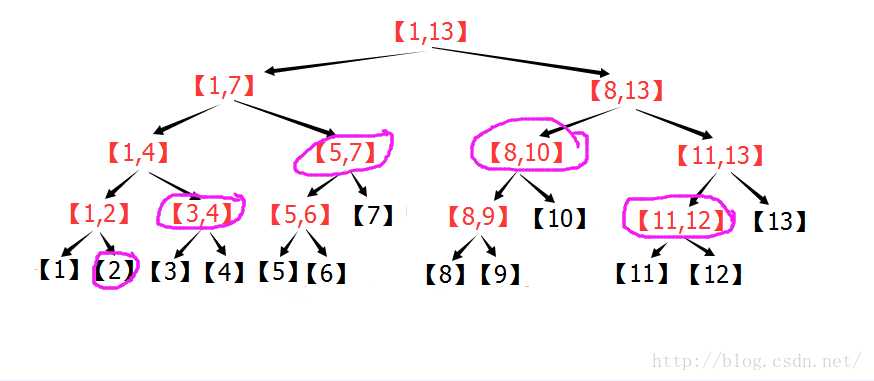
由图可以看出：在n=13的线段树中，[2,12]=[2] + [3,4] + [5,7] + [8,10] + [11,12] 。

分解方法二：自上而下分解——利于计算

 

 

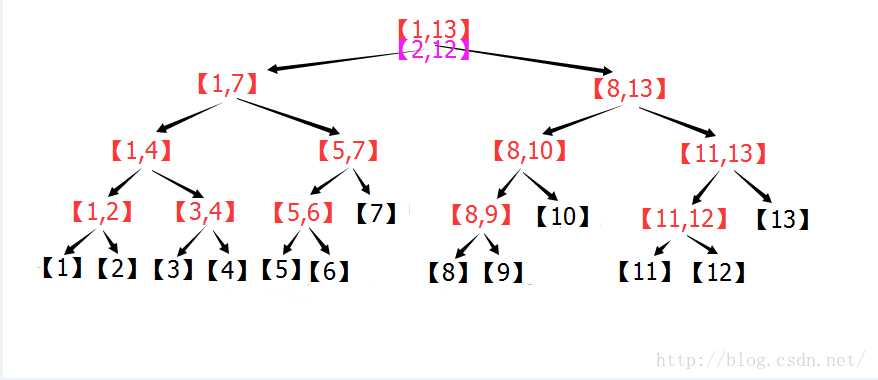
 首先对于区间[1,13]，计算(1+13)/2 = 7，于是将区间[2,12]“切割”成了[2,7]和[8,12]。

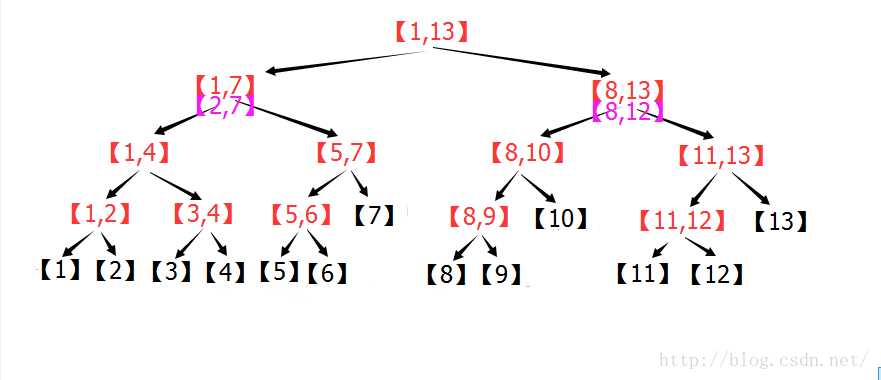
其中[2,7]处于节点[1,7]的位置，[2,7] < [1,7] 所以继续分解，计算(1+7)/2 = 4, 于是将[2,7] 切割成[2,4]和[5,7]。

 

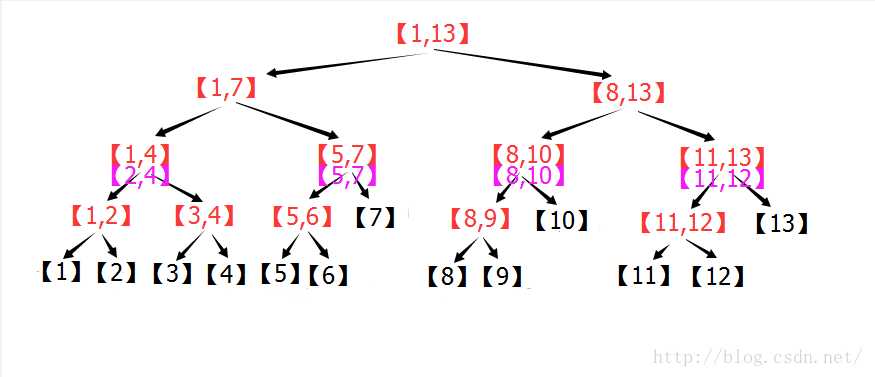
 [5,7]处于节点[5,7]的位置，所以不用继续分解，[2,4]处于区间[1,4]的位置，所以继续分解成[2]和[3,4]。

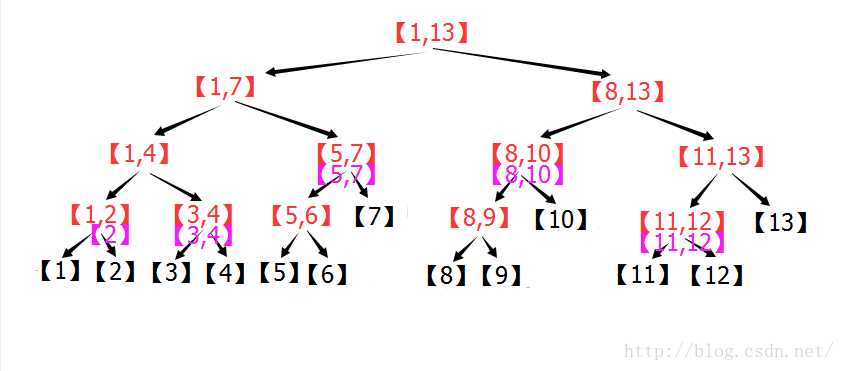
最后【2】 < 【1,2】，所以计算(1+2)/2=1 ，将【2】用1切割，左侧为空，右侧为【2】

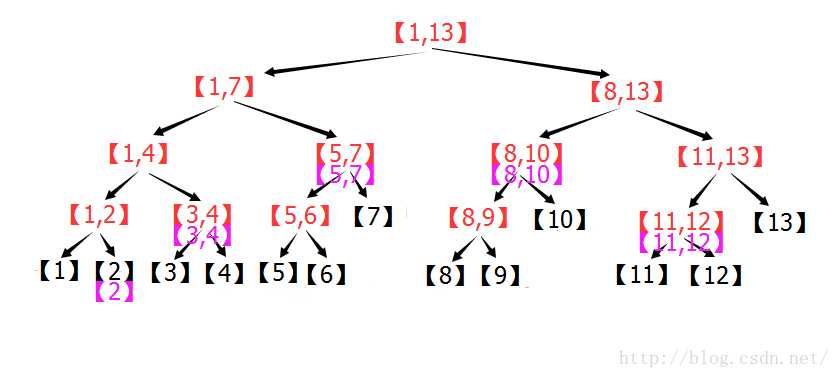
当然程序是递归计算的，不是一层一层计算的，上图只表示计算方法，不代表计算顺序。

 -----------------------------------------------------------------------------------------------------------------感谢诗鸿提供的博客图片。