HDU5909 树形DP + FWT

Posted 2022-04-24 hugh-locke

http://acm.hdu.edu.cn/showproblem.php?pid=5909

题意:给一棵树每个点有权值，树的权值定义为所有节点的异或和，依次询问树里有多少子树的权值是k, (0 <= k < m)

 

先考虑朴素算法，用dp[i][j]表示i这个点异或为j的子树有多少，每加入一颗t的子树v就通过枚举t的树权值和v的树权值，用Om²的复杂度更新dp,那么总的时间复杂度就是nm²

#include <map>
#include <set>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <string>
#include <bitset>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <functional>
using namespace std;
#define For(i, x, y) for(int i=x;i<=y;i++)  
#define _For(i, x, y) for(int i=x;i>=y;i--)
#define Mem(f, x) memset(f,x,sizeof(f))  
#define Sca(x) scanf("%d", &x)
#define Sca2(x,y) scanf("%d%d",&x,&y)
#define Sca3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define Scl(x) scanf("%lld",&x)  
#define Pri(x) printf("%d\\n", x)
#define Prl(x) printf("%lld\\n",x)  
#define CLR(u) for(int i=0;i<=N;i++)u[i].clear();
#define LL long long
#define ULL unsigned long long  
#define mp make_pair
#define PII pair<int,int>
#define PIL pair<int,long long>
#define PLL pair<long long,long long>
#define pb push_back
#define fi first
#define se second 
typedef vector<int> VI;
int read()int x = 0,f = 1;char c = getchar();while (c<‘0‘ || c>‘9‘)if (c == ‘-‘) f = -1;c = getchar();
while (c >= ‘0‘&&c <= ‘9‘)x = x * 10 + c - ‘0‘;c = getchar();return x*f;
const double eps = 1e-9;
const int maxn = 1010;
const int maxm = 1200;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7; 
int N,M,K;
struct Edge
    int to,next;
edge[maxn << 2];
int head[maxn],tot;
void init()
    for(int i = 0 ; i <= N ; i ++) head[i] = -1;
    tot = 0;

void add(int u,int v)
    edge[tot].to = v;
    edge[tot].next = head[u];
    head[u] = tot++;

int val[maxn];
int dp[maxn][maxm],dp2[maxn][maxm],ans[maxm];
void dfs(int t,int la)
    dp[t][val[t]] = 1;
    for(int i = head[t]; ~i ; i = edge[i].next)
        int v = edge[i].to;
        if(v == la) continue;
        dfs(v,t);
        for(int j = 0 ; j < M ; j ++)
            for(int k = 0 ; k < M ; k ++)
                dp2[t][j ^ k] += dp[t][j] * dp[v][k];
            
        
        for(int j = 0 ; j < M ; j ++)
            dp[t][j] += dp2[t][j];
            dp2[t][j] = 0;
        
    
    for(int i = 0 ; i < M ; i ++) ans[i] += dp[t][i];

int main()
    int T; Sca(T);
    while(T--)
        Sca2(N,M); init();
        for(int i = 0 ; i <= N ; i ++)
            for(int j = 0 ; j <= M ; j ++) dp[i][j] = dp2[i][j] = 0;
        
        for(int i = 0 ; i < M; i ++) ans[i] = 0;
        for(int i = 1; i <= N ; i ++) Sca(val[i]);
        for(int i = 1; i <= N - 1; i ++)
            int u,v; Sca2(u,v);
            add(u,v); add(v,u);
        
        dfs(1,-1);
        for(int i = 0 ; i < M; i ++)
            printf("%d ",ans[i]);
        
        puts("");
    
    return 0;

TLE的朴素算法

 

然后我们考虑去优化这层m²,发现这事实上是一个形如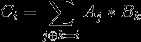的逻辑运算卷积，可以上FWT优化为nmlogm，就可以了

 

这题的正解应该是树分治,回头补图论的时候来把树分治代码补上,FWT像是卡常卡过去的,交GCC能过交C++就TLE

#include <map>
#include <set>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <string>
#include <bitset>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <functional>
using namespace std;
#define For(i, x, y) for(int i=x;i<=y;i++)  
#define _For(i, x, y) for(int i=x;i>=y;i--)
#define Mem(f, x) memset(f,x,sizeof(f))  
#define Sca(x) scanf("%d", &x)
#define Sca2(x,y) scanf("%d%d",&x,&y)
#define Sca3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define Scl(x) scanf("%lld",&x)  
#define Pri(x) printf("%d\\n", x)
#define Prl(x) printf("%lld\\n",x)  
#define CLR(u) for(int i=0;i<=N;i++)u[i].clear();
#define LL long long
#define ULL unsigned long long  
#define mp make_pair
#define PII pair<int,int>
#define PIL pair<int,long long>
#define PLL pair<long long,long long>
#define pb push_back
#define fi first
#define se second 
typedef vector<int> VI;
int read()int x = 0,f = 1;char c = getchar();while (c<‘0‘ || c>‘9‘)if (c == ‘-‘) f = -1;c = getchar();
while (c >= ‘0‘&&c <= ‘9‘)x = x * 10 + c - ‘0‘;c = getchar();return x*f;
const double eps = 1e-9;
const int maxn = 1010;
const int maxm = 1200;
const int INF = 0x3f3f3f3f;
const LL mod = 1e9 + 7; 
LL inv2 = mod + 1 >> 1;
int N,M,K;
struct Edge
    int to,next;
edge[maxn << 2];
int head[maxn],tot;
void init()
    for(int i = 0 ; i <= N ; i ++) head[i] = -1;
    tot = 0;

void add(int u,int v)
    edge[tot].to = v;
    edge[tot].next = head[u];
    head[u] = tot++;

int val[maxn];
LL dp[maxn][maxm],tmp[maxm],ans[maxm];
inline LL add(LL a,LL b)
    return ((a + b) % mod + mod) % mod;

inline LL mul(LL a,LL b)
    return (a % mod * b % mod + mod) % mod;

void FWT(int limit,LL *a,int op)
    for(int i = 1; i < limit; i <<= 1)
        for(int p = i << 1,j = 0; j < limit ; j += p)
            for(int k = 0 ; k < i; k ++)
                LL x = a[j + k],y = a[i + j + k];
                a[j + k] = add(x,y); a[i + j + k] = add(x,-y);
                if(op == -1) a[j + k] = mul(a[j + k],inv2),a[i + j + k] = mul(a[i + j + k],inv2);
            
        
    

void dfs(int t,int la)
    dp[t][val[t]] = 1;
    for(int i = head[t]; ~i ; i = edge[i].next)
        int v = edge[i].to;
        if(v == la) continue;
        dfs(v,t);
        for(int j = 0 ; j < M; j ++) tmp[j] = dp[t][j];
        FWT(M,tmp,1); FWT(M,dp[v],1);
        for(int j = 0 ; j < M ; j ++) tmp[j] = mul(tmp[j],dp[v][j]);
        FWT(M,tmp,-1);
        for(int j = 0 ; j < M ; j ++) dp[t][j] = add(tmp[j],dp[t][j]);
    
    for(int i = 0 ; i < M ; i ++) ans[i] = add(ans[i],dp[t][i]);

int main()
    int T; Sca(T);
    while(T--)
        Sca2(N,M); init();
        for(int i = 0 ; i <= N ; i ++)
            for(int j = 0 ; j <= M ; j ++) dp[i][j] = 0;
        
        for(int i = 0; i < M; i ++) ans[i] = tmp[i] = 0;
        for(int i = 1; i <= N ; i ++) val[i] = read();
        for(int i = 1; i <= N - 1; i ++)
            int u,v; u = read(); v = read();
            add(u,v); add(v,u);
        
        dfs(1,-1);
        for(int i = 0 ; i < M; i ++) printf("%d%c",ans[i],i == M - 1?‘\\n‘:‘ ‘);
    
    return 0;