Gorgeous Sequence（线段树）

Posted 2022-04-18 dwvictor

Gorgeous Sequence

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 6946    Accepted Submission(s): 1784

Problem Description

There is a sequence a of length n. We use ai to denote the i-th element in this sequence. You should do the following three types of operations to this sequence.

0 x y t: For every x≤i≤y, we use min(ai,t) to replace the original ai‘s value.
1 x y: Print the maximum value of ai that x≤i≤y.
2 x y: Print the sum of ai that x≤i≤y.

 

 

Input

The first line of the input is a single integer T, indicating the number of testcases. 

The first line contains two integers n and m denoting the length of the sequence and the number of operations.

The second line contains n separated integers a1,…,an (∀1≤i≤n,0≤ai<231).

Each of the following m lines represents one operation (1≤x≤y≤n,0≤t<231).

It is guaranteed that T=100, ∑n≤1000000, ∑m≤1000000.

 

 

Output

For every operation of type 1 or 2, print one line containing the answer to the corresponding query.

 

 

Sample Input

1 5 5 1 2 3 4 5 1 1 5 2 1 5 0 3 5 3 1 1 5 2 1 5

 

 

Sample Output

5 15 3 12

Hint

Please use efficient IO method

 

 

Author

XJZX

 

 

Source

2015 Multi-University Training Contest 2

 

 

Recommend

wange2014   |   We have carefully selected several similar problems for you:  6554 6553 6552 6551 6550 

 

题意 ：

有一个长度为n的序列a。我们用ai来表示这个序列中的第i个元素。您应该对这个序列执行以下三种类型的操作。

 

0 x y t:对于每一个x≤i≤y，我们用min(ai,t)替换原始ai的值。

1 x y:打印ai的最大值，即x≤i≤y。

2xy:输出x≤i≤y的ai之和。

 

 

输入

输入的第一行是一个整数T，表示测试用例的数量。

 

第一行包含两个整数n和m，表示序列的长度和操作的数量。

 

第二行包含n分离整数a1,…,一个(∀1≤≤n, 0≤ai < 231)。

 

以下m行每一行表示一个操作(1≤x≤y≤n,0≤t<231)。

 

保证T=100，∑n≤1000000，∑m≤1000000。

 

 

输出

对于类型1或2的每个操作，打印一行包含相应查询的答案。

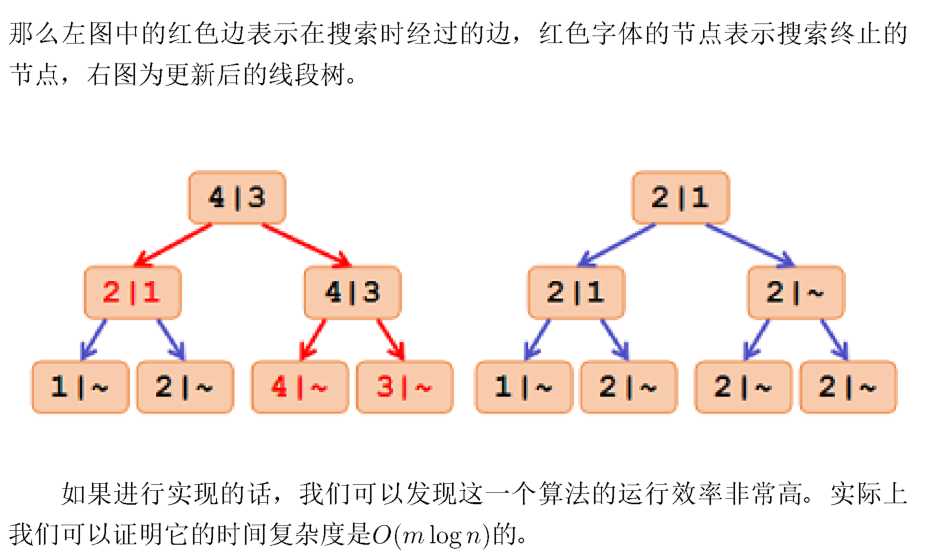
题解：

 

 

c++代码

 

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 7;
int a[maxn];
#define EF if(ch==EOF) return x;
// #define lc k<<1
// #define rc k<<1|1
inline int read()
    int x=0,f=1;char ch=getchar();
    while(ch<‘0‘||ch>‘9‘)if(ch==‘-‘)f=-1;EF;ch=getchar();
    while(ch>=‘0‘&&ch<=‘9‘)x=x*10+ch-‘0‘;ch=getchar();
    return x*f;

struct tree

    int l , r;
    int miax , maxx;
    ll sum;
    int set_lazy;
t[maxn << 2];


// inline void push_up(int k)
//     // sum[k]=sum[lc]+sum[rc];
//     // mx[k]=max(mx[lc],mx[rc]);
//     // se[k]=max(se[lc],se[rc]);
//     // mc[k]=0;
//     // if(mx[lc]!=mx[rc]) se[k]=max(se[k],min(mx[lc],mx[rc]));
//     // if(mx[k]==mx[lc]) mc[k]+=mc[lc];
//     // if(mx[k]==mx[rc]) mc[k]+=mc[rc];
//     t[k].sum = t[lc].sum + t[rc].sum;
//     t[k].maxx = max(t[lc].maxx,t[rc].maxx);
//     t[k].miax = max(t[lc].miax,t[rc].miax);
//     t[k].set_lazy = 0;
//     if(t[lc].maxx != t[rc].maxx) t[k].miax = max(t[k].miax,min(t[lc].maxx,t[rc].maxx));
//     if(t[k].maxx == t[lc].maxx) t[k].set_lazy += t[lc].set_lazy;
//     if(t[k].maxx == t[rc].maxx) t[k].set_lazy += t[rc].set_lazy;

// 
inline void push_up(int rt)
    t[rt].sum = t[rt << 1].sum + t[rt << 1|1].sum;
   // t[rt].minn = min(t[rt << 1].minn,t[rt << 1|1].minn);
    t[rt].maxx = max(t[rt << 1].maxx,t[rt << 1|1].maxx);
    t[rt].miax = max(t[rt << 1].miax, t[rt << 1|1].miax);
    t[rt].set_lazy = 0;
    if(t[rt << 1].maxx != t[rt <<1|1].maxx) t[rt].miax = max(t[rt].miax,min(t[rt << 1].maxx , t[rt <<1|1].maxx));
    //打上标记，记录下标记个数
    if(t[rt].maxx == t[rt << 1].maxx) t[rt].set_lazy += t[rt << 1].set_lazy;
    if(t[rt].maxx == t[rt << 1|1].maxx) t[rt].set_lazy += t[rt << 1|1].set_lazy;
   // cout << t[rt].sum << " " << rt <<endl;


inline void dec_tag(int rt,int v)
    if(v >= t[rt].maxx) return;
    t[rt].sum += 1ll * (v - t[rt].maxx)*t[rt].set_lazy;
    t[rt].maxx = v;


inline void push_down(int rt)
    dec_tag(rt << 1,t[rt].maxx);
    dec_tag(rt << 1|1,t[rt].maxx);

  // inline void push_down(int rt) 
  //       if(t[rt].set_lazy)  ///if set_lazy add_lazy = 0
  //           t[rt<<1].set_lazy = t[rt].set_lazy;
  //           t[rt<<1].sum = (t[rt<<1].r - t[rt<<1].l + 1) * t[rt].set_lazy;
  //           t[rt<<1].maxx = t[rt].set_lazy;
  //           t[rt<<1].minn = t[rt].set_lazy;
  //           t[rt<<1|1].set_lazy = t[rt].set_lazy;
  //           t[rt<<1|1].sum = (t[rt<<1|1].r - t[rt<<1|1].l + 1) * t[rt].set_lazy;
  //           t[rt<<1|1].maxx = t[rt].set_lazy;
  //           t[rt<<1|1].minn = t[rt].set_lazy;
  //           //tre[rt].add_lazy = 0;
  //           //tre[rt<<1].add_lazy = tre[rt<<1|1].add_lazy = 0;
  //           t[rt].set_lazy = 0;
  //           return ;
  //       
  //       // if(tre[rt].add_lazy) 
  //       //     tre[rt<<1].add_lazy += tre[rt].add_lazy;
  //       //     tre[rt<<1].sum += (tre[rt<<1].r - tre[rt<<1].l + 1) * tre[rt].add_lazy;
  //       //     tre[rt<<1].max += tre[rt].add_lazy;
  //       //     tre[rt<<1].min += tre[rt].add_lazy;
  //       //     tre[rt<<1|1].add_lazy += tre[rt].add_lazy;
  //       //     tre[rt<<1|1].sum += (tre[rt<<1|1].r - tre[rt<<1|1].l + 1) *
  //       //                         tre[rt].add_lazy;
  //       //     tre[rt<<1|1].max += tre[rt].add_lazy;
  //       //     tre[rt<<1|1].min += tre[rt].add_lazy;
  //       //     tre[rt].add_lazy = 0;
  //       // 
  //   

void build(int rt,int l ,int r)
    t[rt].l = l, t[rt].r = r;
    //t[rt].set_lazy = 1;

    if(l == r)
        t[rt].sum =  t[rt].maxx = a[l];
        t[rt].miax = -1;
        t[rt].set_lazy = 1;
       // cout <<"nbb  " <<t[rt].sum << " "<<rt << endl;
        return;
    
    int mid = (l + r) >> 1;
    build(rt <<1,l,mid);
    build(rt << 1|1,mid + 1,r);
    push_up(rt);


void up_date(int rt,int l,int r,int d)
    if(d >= t[rt].maxx) return;

    //push_down(rt);
    if(l <= t[rt].l && r >= t[rt].r && d > t[rt].miax)
     // t[rt].sum = (t[rt].r - t[rt].l + 1) * d;
     // t[rt].maxx = d;
     // t[rt].minn = d;
     // t[rt].set_lazy = d;
     dec_tag(rt,d);
     return;
 
 push_down(rt);
 int mid = (t[rt].l + t[rt].r) >> 1;
 if(r <= mid) 
    up_date(rt<<1,l,r,d);
 else if(l > mid) 
    up_date(rt<<1|1,l,r,d);
 else 
    up_date(rt<<1,l,mid,d);
    up_date(rt<<1|1,mid+1,r,d);

push_up(rt);






 ll query_sum(int rt,int l,int r)  ///sum

    if(l <= t[rt].l && t[rt].r <= r) 
        return t[rt].sum;
    
    push_down(rt);
    int mid = (t[rt].l + t[rt].r) >> 1;
    if(r <= mid) 
        return query_sum(rt<<1,l,r);
     else if(l > mid) 
        return query_sum(rt<<1|1,l,r);
     else 
        return query_sum(rt<<1,l,mid) + query_sum(rt<<1|1,mid+1,r);
    


    int query_max(int rt,int l,int r)  ///max

       //cout << t[rt].maxx  << endl;
        if(l <= t[rt].l && t[rt].r <= r) 
            return t[rt].maxx;
        
        push_down(rt);
        int mid = (t[rt].l + t[rt].r) >> 1;
        if(r <= mid) 
            return query_max(rt<<1,l,r);
         else if(l > mid) 
            return query_max(rt<<1|1,l,r);
         else 
            return max(query_max(rt<<1,l,mid), query_max(rt<<1|1,mid+1,r));
        
    
    // int query_min(int rt,int l,int r)  ///min
    //     push_down(rt);
    
    //     if(l <= t[rt].l && t[rt].r <= r) 
    //         return t[rt].minn;
    //     
    //     int mid = (t[rt].l + t[rt].r) >> 1;
    //     if(r <= mid) 
    //         return query_min(rt<<1,l,r);
    //      else if(l > mid) 
    //         return query_min(rt<<1|1,l,r);
    //      else 
    //         return min(query_min(rt<<1,l,mid), query_min(rt<<1|1,mid+1,r));
    //     
    // 


    int main(int argc, char const *argv[])
    
        int t;
        //scanf("%d",&t);
        t = read();
        while(t--)
            int n , q;
            //scanf("%d%d",&n,&q);
            n = read(),q = read();
            for(int i = 1;i <= n; i++) //scanf("%d",&a[i]);
                a[i] = read();
            build(1,1,n);
   // //0 cout << 1;
   //  for(int i = 1;i <= n; i++)
   //      cout << t[i].maxx ;
   //  
            while(q--)
                int a,b,c;
                //scanf("%d%d%d",&a,&b,&c);
                a = read() ,b = read() , c = read();
                if(a == 0)
                    int z;
                    //scanf("%d",&z);
                    z = read();
                    
                    up_date(1,b,c,z);
                
                else if(a == 1)
                    printf("%d\\n",query_max(1,b,c));
                
                else
                    printf("%lld\\n",query_sum(1,b,c));
                
            
        
        return 0;
    

View Code