《DSP using MATLAB》Problem 8.10
Posted ky027wh-sx
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《DSP using MATLAB》Problem 8.10相关的知识,希望对你有一定的参考价值。

代码:
%% ------------------------------------------------------------------------ %% Output Info about this m-file fprintf(‘\\n***********************************************************\\n‘); fprintf(‘ <DSP using MATLAB> Problem 8.10 \\n\\n‘); banner(); %% ------------------------------------------------------------------------ %a0 = 0.90; %a0 = 0.95; a0 = 0.99; % digital iir 1st-order allpass filter b = [a0 1]; a = [1 a0]; figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘Problem 8.10 Pole-Zero Plot‘) set(gcf,‘Color‘,‘white‘); zplane(b,a); title(sprintf(‘Pole-Zero Plot, r=%.2f‘,a0)); %pzplotz(b,a); [db, mag, pha, grd, w] = freqz_m(b, a); % --------------------------------------------------------------------- % Choose the gain parameter of the filter, maximum gain is equal to 1 % --------------------------------------------------------------------- gain1=max(mag) % with poles K = 1 [db, mag, pha, grd, w] = freqz_m(K*b, a); figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘Problem 8.10 IIR allpass filter‘) set(gcf,‘Color‘,‘white‘); subplot(2,2,1); plot(w/pi, db); grid on; axis([0 2 -60 10]); set(gca,‘YTickMode‘,‘manual‘,‘YTick‘,[-60,-30,0]) set(gca,‘YTickLabelMode‘,‘manual‘,‘YTickLabel‘,[‘60‘;‘30‘;‘ 0‘]); set(gca,‘XTickMode‘,‘manual‘,‘XTick‘,[0,0.25,0.5,1,1.5,1.75,2]); xlabel(‘frequency in \\pi units‘); ylabel(‘Decibels‘); title(‘Magnitude Response in dB‘); subplot(2,2,3); plot(w/pi, mag); grid on; %axis([0 1 -100 10]); xlabel(‘frequency in \\pi units‘); ylabel(‘Absolute‘); title(‘Magnitude Response in absolute‘); set(gca,‘XTickMode‘,‘manual‘,‘XTick‘,[0,0.25,0.5,1,1.5,1.75,2]); set(gca,‘YTickMode‘,‘manual‘,‘YTick‘,[0,1.0]); subplot(2,2,2); plot(w/pi, pha); grid on; %axis([0 1 -100 10]); xlabel(‘frequency in \\pi units‘); ylabel(‘Rad‘); title(‘Phase Response in Radians‘); subplot(2,2,4); plot(w/pi, grd*pi/180); grid on; %axis([0 1 -100 10]); xlabel(‘frequency in \\pi units‘); ylabel(‘Rad‘); title(‘Group Delay‘); set(gca,‘XTickMode‘,‘manual‘,‘XTick‘,[0,0.25,0.5,1,1.5,1.75,2]); %set(gca,‘YTickMode‘,‘manual‘,‘YTick‘,[0,1.0]); figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘Problem 8.10 IIR allpass filter‘) set(gcf,‘Color‘,‘white‘); plot(w/pi, -pha/w); grid on; %axis([0 1 -100 10]); xlabel(‘frequency in \\pi units‘); ylabel(‘Rad‘); title(‘Phase Delay in samples‘); % Impulse Response fprintf(‘\\n----------------------------------‘); fprintf(‘\\nPartial fraction expansion method: \\n‘); [R, p, c] = residuez(K*b,a) MR = (abs(R))‘ % Residue Magnitude AR = (angle(R))‘/pi % Residue angles in pi units Mp = (abs(p))‘ % pole Magnitude Ap = (angle(p))‘/pi % pole angles in pi units [delta, n] = impseq(0,0,50); h_chk = filter(K*b,a,delta); % check sequences % ------------------------------------------------------------------------------------------------ % gain parameter K % ------------------------------------------------------------------------------------------------ %h = -0.2111 * ((-0.9) .^ n) + 1.1111 * delta; %r=0.90 %h = -0.1026 * ((-0.95) .^ n) + 1.0526 * delta; %r=0.95 h = -0.0201 * ((-0.99) .^ n) + 1.0101 * delta; %r=0.99 % ------------------------------------------------------------------------------------------------ figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘Problem 8.10 IIR allpass filter, h(n) by filter and Inv-Z ‘) set(gcf,‘Color‘,‘white‘); subplot(2,1,1); stem(n, h_chk); grid on; %axis([0 2 -60 10]); xlabel(‘n‘); ylabel(‘h\\_chk‘); title(‘Impulse Response sequences by filter‘); subplot(2,1,2); stem(n, h); grid on; %axis([0 1 -100 10]); xlabel(‘n‘); ylabel(‘h‘); title(‘Impulse Response sequences by Inv-Z‘); [db, mag, pha, grd, w] = freqz_m(h, 1); figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘Problem 8.10 IIR filter, h(n) by Inv-Z ‘) set(gcf,‘Color‘,‘white‘); subplot(2,2,1); plot(w/pi, db); grid on; axis([0 2 -60 10]); set(gca,‘YTickMode‘,‘manual‘,‘YTick‘,[-60,-30,0]) set(gca,‘YTickLabelMode‘,‘manual‘,‘YTickLabel‘,[‘60‘;‘30‘;‘ 0‘]); set(gca,‘XTickMode‘,‘manual‘,‘XTick‘,[0,0.25,1,1.75,2]); xlabel(‘frequency in \\pi units‘); ylabel(‘Decibels‘); title(‘Magnitude Response in dB‘); subplot(2,2,3); plot(w/pi, mag); grid on; %axis([0 1 -100 10]); xlabel(‘frequency in \\pi units‘); ylabel(‘Absolute‘); title(‘Magnitude Response in absolute‘); set(gca,‘XTickMode‘,‘manual‘,‘XTick‘,[0,0.25,1,1.75,2]); set(gca,‘YTickMode‘,‘manual‘,‘YTick‘,[0,1.0]); subplot(2,2,2); plot(w/pi, pha); grid on; %axis([0 1 -100 10]); xlabel(‘frequency in \\pi units‘); ylabel(‘Rad‘); title(‘Phase Response in Radians‘); subplot(2,2,4); plot(w/pi, grd*pi/180); grid on; %axis([0 1 -100 10]); xlabel(‘frequency in \\pi units‘); ylabel(‘Rad‘); title(‘Group Delay‘); set(gca,‘XTickMode‘,‘manual‘,‘XTick‘,[0,0.25,1,1.75,2]); %set(gca,‘YTickMode‘,‘manual‘,‘YTick‘,[0,1.0]);
运行结果:
第1、2小题的图这里不放了。
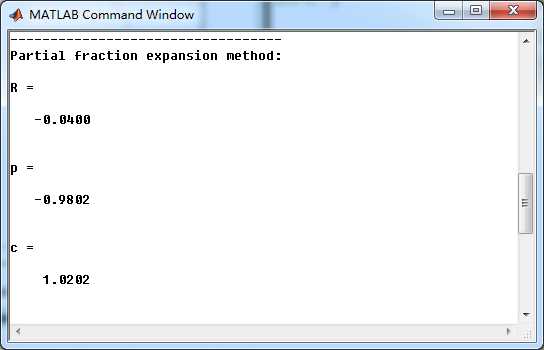
相位延迟phase-delay为0.01时对应的a 的值0.9802
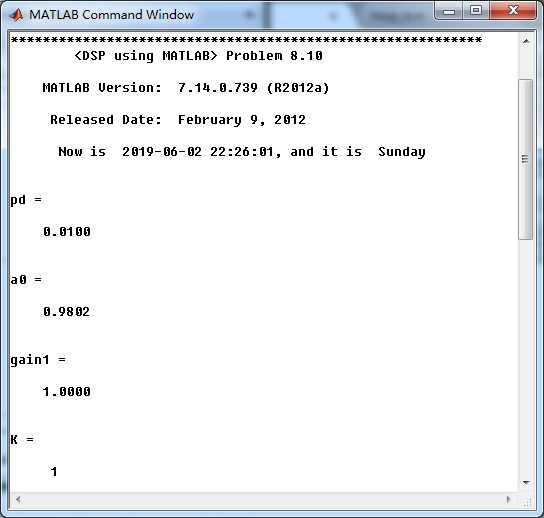
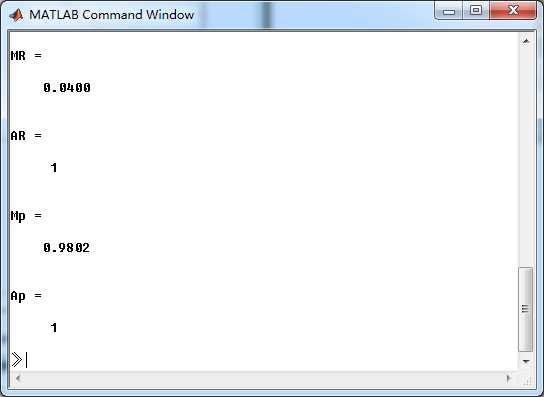
此时1阶全通系统的留数、极点为
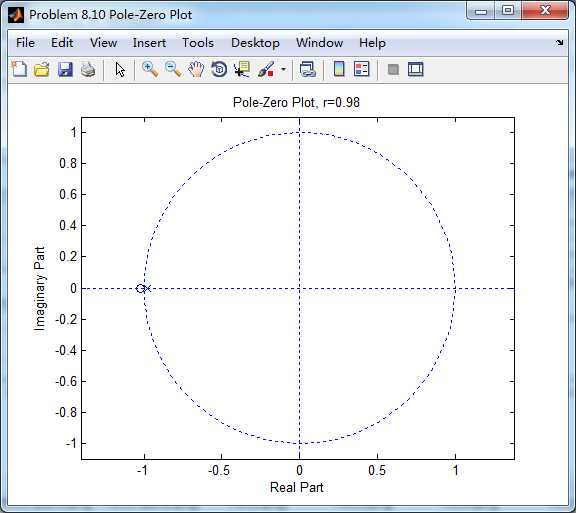
系统零极点图
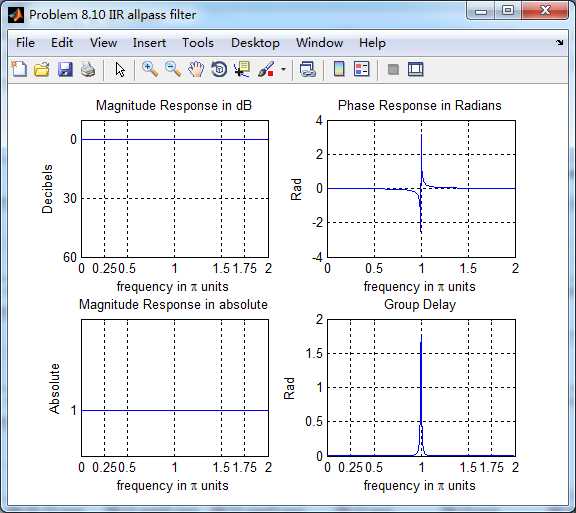
该系统部分分式展开后,求逆z变换得脉冲响应
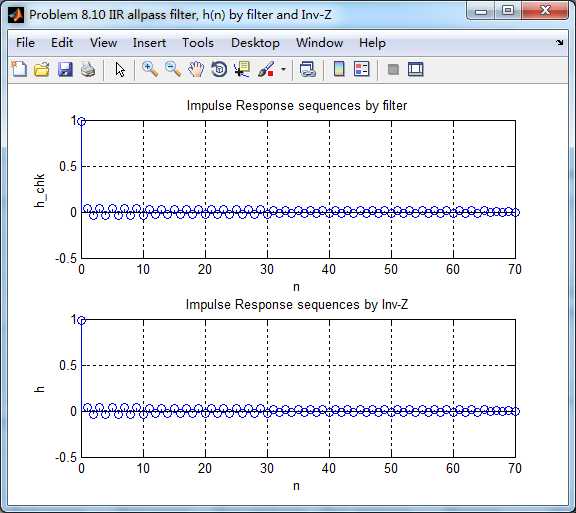
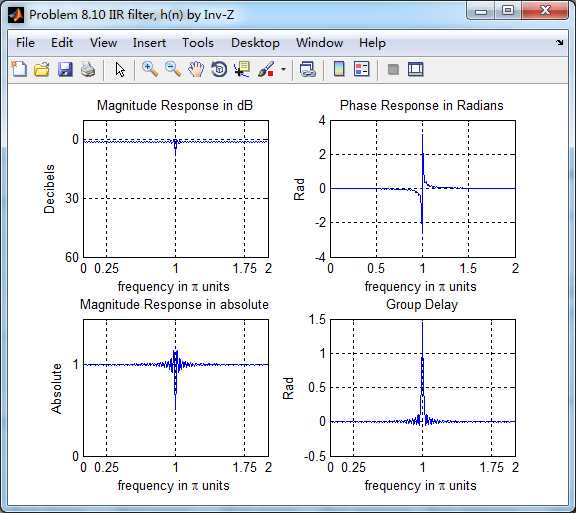
由下图知,两种方法得到的系统脉冲响应h的幅度谱、相位谱、群延迟大致类似(ω=π时不同)。
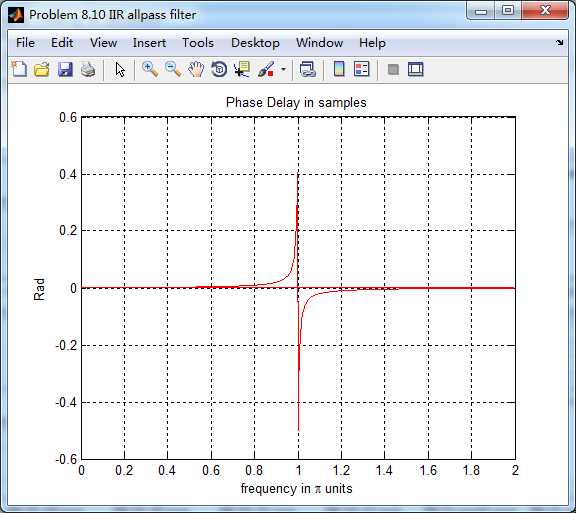
以上是关于《DSP using MATLAB》Problem 8.10的主要内容,如果未能解决你的问题,请参考以下文章
《DSP using MATLAB》Problem 3.12