第7章小结

Posted 2021-12-16 ilikezero

第七章小结 查找

 

   根据这一章的题目，显而易见，这一张讲的是查找。虽然在之前的学习中，我们已经解除了不少的查找功能，但事实上，查找是一个可复杂可简单的过程。我们之前接触的查找大多数都比较的简单，而在学习完这一章后，我们会发现，事实上查找有很多种办法，也会发现，不同的情况，不同的存储结构都需要不同的查找方法。

 

以下为一些查找的概念和术语：

①关键字：数据元素（记录）中某个数据项的值，用它可以表示一个数据元素。

 

②动态查找表/静态查找表：若在查找的过程中进行修改操作（插入或删除），则相应的表为动态查找表，否则为静态查找表。

 

③平均查找长度：为确定记录在查找表中的位置，需和给定值进行比较的关键字个数的期望值称为查找算法在查找成功时的平均查找长度。公式如下：ASL=∑PiCi (i=1,2,3,…,n),可以简单以数学上的期望来这么理解。其中：Pi 为查找表中第i个数据元素的概率，Ci为找到第i个数据元素时已经比较过的次数。

 

下图为本章的主要结构：

 

 

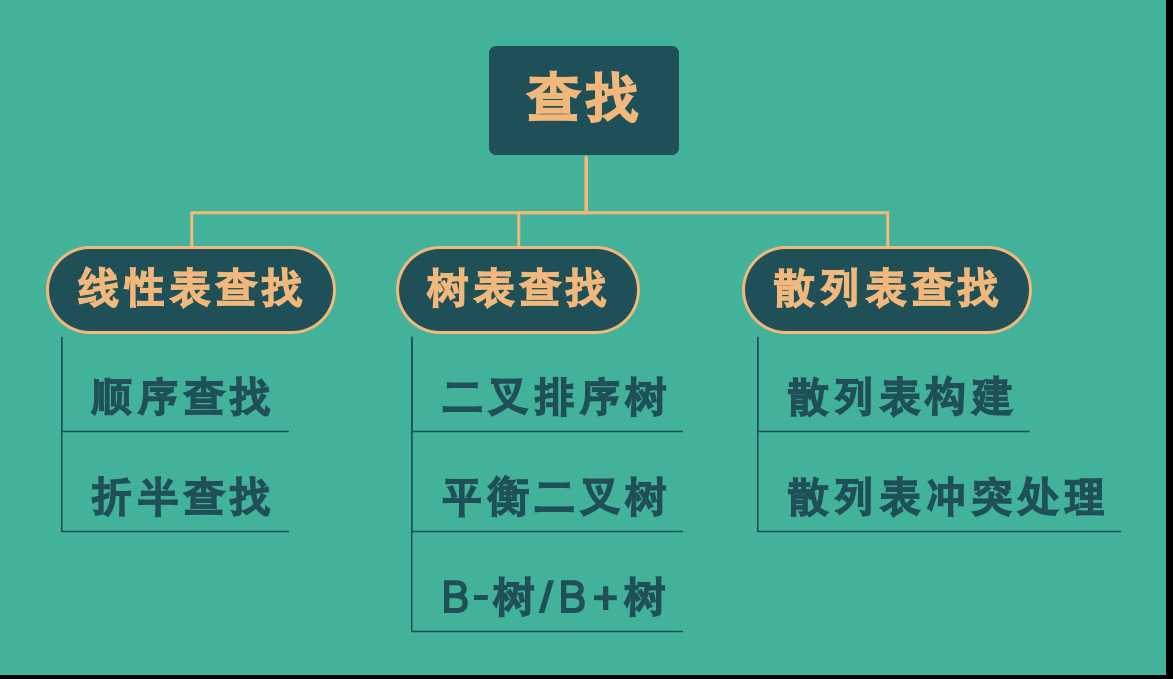
线性表查找：

 

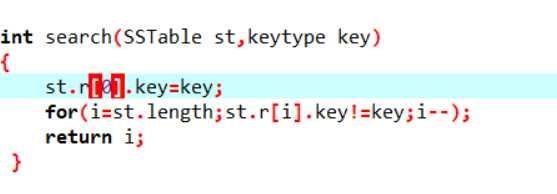
顺序查找：

从表的一端开始查找，依次将记录的关键字与给定的值进行比较，若有相等的则为成功，否则失败。这个是比较简单的。本章中引进了“哨兵”概念。可以免去查找过程中每一步都需要检测整个表是否查找完毕。

 

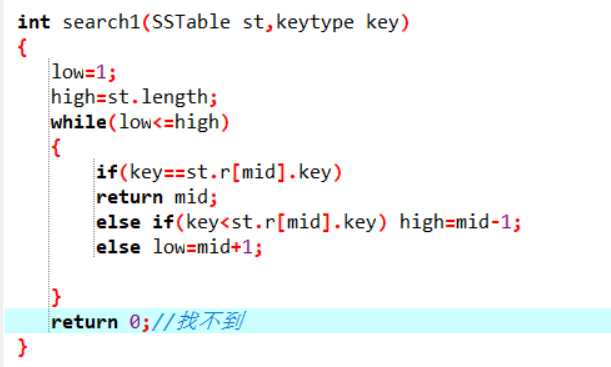
折半查找：搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

树表的查找：

 

二叉排序树：

性质：

（1）若左子树不空，则左子树上所有节点的值均小于它的根节点的值；

（2）若右子树不空，则右子树上所有节点的值均大于它的根节点的值；

（3）左、右子树也分别为二叉排序树；

 

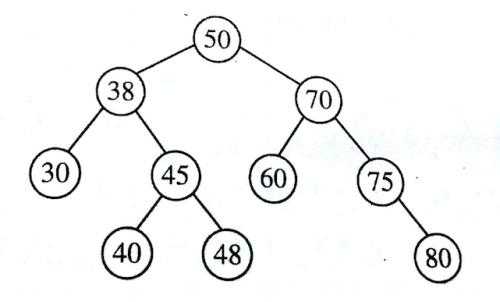
二叉树的查找和插入都比较的简单，采用递归的方法就可以实现了。比较难搞定的是删除的操作，由于有不同的情况，所以也要应不不同的对付措施。在二叉排序树删去一个结点，分三种情况讨论：

 

若*p结点为叶子结点，即PL(左子树)和PR(右子树)均为空树。由于删去叶子结点不破坏整棵树的结构，则可以直接删除此子结点。

若*p结点只有左子树PL或右子树PR，此时只要令PL或PR直接成为其双亲结点*f的左子树（当*p是左子树）或右子树（当*p是右子树）即可，作此修改也不破坏二叉排序树的特性。

若*p结点的左子树和右子树均不空。在删去*p之后，为保持其它元素之间的相对位置不变，可按中序遍历保持有序进行调整，可以有两种做法：

其一是令*p的左子树为*f的左/右(依*p是*f的左子树还是右子树而定)子树，*s为*p左子树的最右下的结点，而*p的右子树为*s的右子树；

其二是令*p的直接前驱（或直接后继）替代*p，然后再从二叉排序树中删去它的直接前驱（或直接后继）－即让*f的左子树(如果有的话)成为*p左子树的最左下结点(如果有的话)，再让*f成为*p的左右结点的父结点。

 

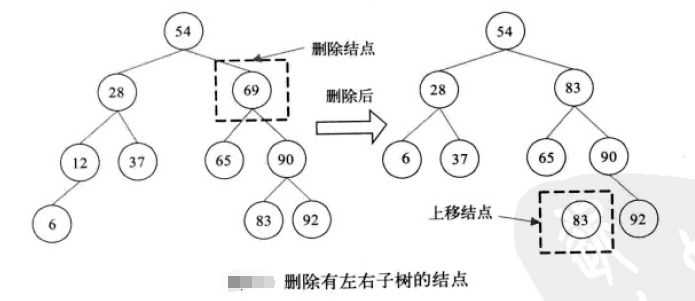
每个结点的C(i)为该结点的层次数。最坏情况下，当先后插入的关键字有序时，构成的二叉排序树蜕变为单支树，树的深度为其平均查找长度(n+1)/2(和顺序查找相同），最好的情况是二叉排序树的形态和折半查找的判定树相同，其平均查找长度和log 2 (n)成正比。

 

因此为了避免这种情况，引出了平衡二叉树的概念。

 

平衡二叉树：

它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

 

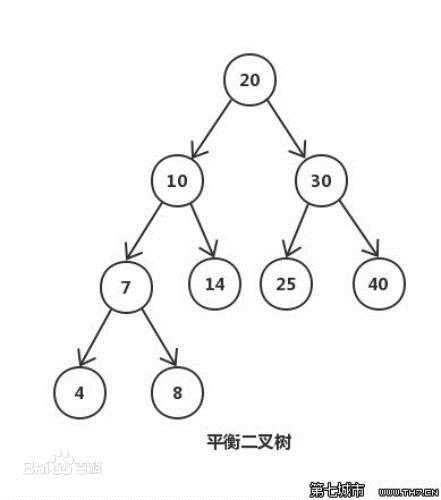
然而当数据量很大的时候，二叉树满足不了要求，这时候又提出了B树。

 

B树/B+树：

 

具体结构如下图：

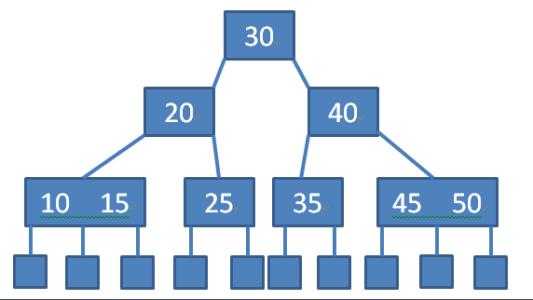
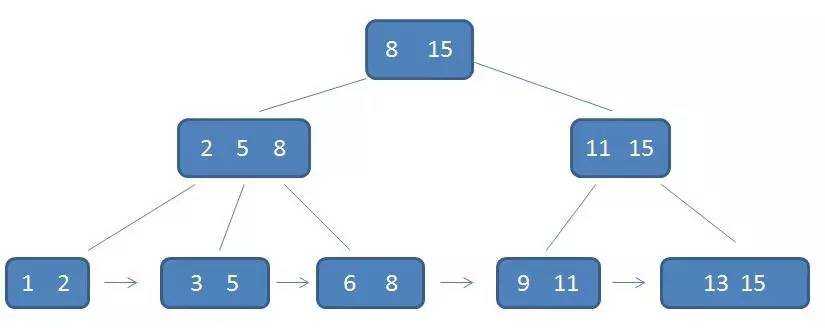
其中B+树的理解，这一篇博客以图文的形式很好地诠释了。https://blog.csdn.net/qq_26222859/article/details/80631121

 

 

最后还有散列表：

 

在进行查找时，在记录的存储位置与它的关键字之间建立一个确定的对应关系h,以线性表中每个元素的关键字K为自变量，通过函数h(K)计算出该元素的存储位置，我们将h函数称为散列函数或哈希函数。这种查找方法称为散列查找。

 

散列函数：

构造散列函数的目标是使散列地址尽可能均匀分布在散列空间上，同时使计算尽可能简单，以节省计算时间。

①直接定址法

以关键字K本身或关键字加上某个数值常量C作为散列地址的方法，对应的散列函数：

h(K)=K+C (C为常数)

②除留余数法

以关键字K除以散列长度m所得余数作为散列地址的方法，对应的散列函数：

h(K)=K%m

③数字分析法

当关键码的位数很多时，可以通过对关键码的各位进行分析，丢掉分布不均的位，留下分布均与的位作为散列值。

④平方取中法

取关键字平方的中间几位作为散列地址的方法，由平方取中法得到的散列地址同关键字的每一位都有关，使得散列地址有较好分散性。

⑤折叠法：

首先将关键字分割成位数相同的几段(最后一段位数可少一些)，然后将它们的叠加和(舍去最高位进位)作为散列地址的方法。

 

但是由于我们使用这些规则（函数）来获得相关下标的信息，难免就会有重复的时候。此时就会产生冲突。由此也有相应的措施来解决冲突的问题。

①开放定址法

思路：从发生冲突的那个单元开始，按照一定次序，从散列表中查找出一个空闲的存储单元，把发生冲突的待插入元素存入到该单元的一类处理冲突的方法：

 

1.线性探查法

是用开放定址法处理冲突的一种最简单的探查方法。

从发生冲突的d单元起,依次探查下一个单元,直到碰到一个空闲单元或探查完所有单元为止探查时,当达到下标为m-1的表尾单元时,下一个探查的单元是下标为0的表首单元。

探查序列为d,d+1,d+2……，表示为(d+i)%m (0≤i≤m-1)。

 

2.平方探查法

探查序列为d,d+1,d+2……,表示为(d+i2)%m(0≤i≤m/2)。

 

②链表地址法

链表地址法为散列表的每个表象建立一个单链表，用于链接同义词表，为此需要给每个表项增加一个指针域。

 

由于这一章的内容实在是太多了，还有很多的细节这里没有注意到。由于实践题最后一个测试点还没有顺利通过，所以这里也没办法进行讲述了。不过总体的思路也有了大概了，可能还是一些细节的问题没有找到。交了就回去看看了。

 

马上就要进入期末的复习阶段了。最近也有点忙。但是接下来的目标就是：

好好整理本学期学习过的内容，做一个比较完整的总结。准备迎接期末了。