SPOJDIVCNT2: Counting Divisors(莫比乌斯反演)

Posted 2020-07-27 GFY

http://acm.tzc.edu.cn/acmhome/vProblemList.do?method=problemdetail&oj=SPOJ&pid=DIVCNT2

给出n求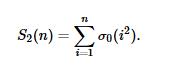

其中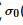是除数函数,0代表0次方.

 

 

 

 

 

 

 1 #include<algorithm>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<cstring>
 5 #include<iostream>
 6 #define ll long long
 7 ll n,sig[100000005],N,a[200005];
 8 int p[10000005];
 9 bool mark[100000005];
10 char mul[100000005];
11 int smu[100000005],L;
12 int read(){
13     int t=0,f=1;char ch=getchar();
14     while (ch<\'0\'||ch>\'9\'){if (ch==\'-\') f=-1;ch=getchar();}
15     while (\'0\'<=ch&&ch<=\'9\'){t=t*10+ch-\'0\';ch=getchar();}
16     return t*f;
17 }
18 ll Read(){
19     ll t=0,f=1;char ch=getchar();
20     while (ch<\'0\'||ch>\'9\'){if (ch==\'-\') f=-1;ch=getchar();}
21     while (\'0\'<=ch&&ch<=\'9\'){t=t*10+ch-\'0\';ch=getchar();}
22     return t*f;
23 }
24 void Init(int n){
25     sig[1]=1;smu[1]=1;mul[1]=1;
26     for (int i=2;i<=n;i++){
27         if (!mark[i]){
28             p[++p[0]]=i;
29             mul[i]=-1;
30             smu[i]=1;
31             sig[i]=2;
32         }
33         for (int j=1;j<=p[0]&&p[j]*i<=n;j++){
34             mark[p[j]*i]=1;
35             if (i%p[j]==0){
36                 sig[p[j]*i]=sig[i]/(smu[i]+1)*(smu[i]+2);
37                 smu[p[j]*i]=smu[i]+1;
38                 mul[p[j]*i]=0;
39                 break;
40             }
41             sig[p[j]*i]=sig[i]*2;
42             smu[p[j]*i]=1;
43             mul[p[j]*i]=-mul[i];
44         }
45     }
46     for (int i=1;i<=n;i++) sig[i]+=sig[i-1],smu[i]=smu[i-1]+std::abs((int)mul[i]);
47 }
48 
49 ll R(ll x){
50     if (x<=L) return sig[x];
51     ll res=0;
52     for (register ll i=1,j;i<=x;i=j+1){
53         j=(x/(x/i));
54         res+=(j-i+1)*(x/i);
55     }
56     return res;
57 }
58 ll Smu(ll x){
59     if (x<=L) return smu[x];
60     ll res=0;
61     for (register ll i=1;i*i<=x;i++)
62      if (mul[i]) res+=mul[i]*(x/(i*i));
63     return res; 
64 }
65 void solve(ll n){
66     int m=sqrt(n);
67     ll ans=0;
68     ll pre=smu[m],tt;
69     for (int i=1;i<=m;i++) if (mul[i]) ans+=R(n/i);
70     for (ll i=m+1,j;i<=n;i=j+1){
71         j=(n/(n/i));
72         tt=Smu(j);
73         ans+=(tt-pre)*(R(n/i));
74         pre=tt;
75     }
76     printf("%lld\\n",ans);
77 }
78 int main(){
79     int T=read();
80     ll mx=0;
81     N=1000000000000;
82     for (int i=1;i<=T;i++) 
83      a[i]=Read(),mx=std::max(mx,a[i]);
84     if (mx<=10000) L=10000;else L=pow(N,2.0/3.0);
85     Init(L);
86     for (int i=1;i<=T;i++){
87         solve(a[i]);
88     }
89 }