映射与函数
Posted liming19680104
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了映射与函数相关的知识,希望对你有一定的参考价值。
集合
不含任何元素的集合称为空集,记作![]()
元素a属于集合M,记作a∈M.
元素a不属于集合M,记作a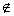 M
M
集合的表示法:

(1)列举法:按某种方式列出集合中的全体元素例:有限集合A={a1,a2…,an} ![]()
自然数集N={0,1,2…,n…} ={n}
(2)描述法:M={x | x所具有的特征}
例:整数集合 Z={x l x∈N 或 -x∈N+}
有理数集 Q={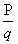 | p∈Z,q∈N+,p与q互质}
| p∈Z,q∈N+,p与q互质}
实数集合 R={x | x为有理数或无理数}

集合之间的关系与运算:
定义设有集合A、B,若x∈A必有x∈B,则称A是B的子集,或称B包含A,或称A包含于B,记作A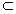 B.
B.
若A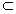 B且B
B且B A,则称A与B相等,记作A=B
A,则称A与B相等,记作A=B
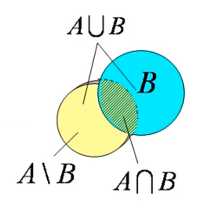
并集 AUB={x|x∈A或x∈B}
交集 A∩B={x|x∈A且x∈B}
差集 A\\B={x|x∈A且x B}
B}
区间与邻域:
区间:是指介于某两个实数之间的全体实数.这两个实数叫做区间的端点.
{x l a<x<b} 称为开区间,记作 (a,b)
![]()
{x l a≤x≤b}称为闭区间,记作[a,b]
![]()
{xla≤x<b}称为半开区间,记作[a,b)
无限区间: [a,+∞)={x|a≤x}
邻域:



映射:
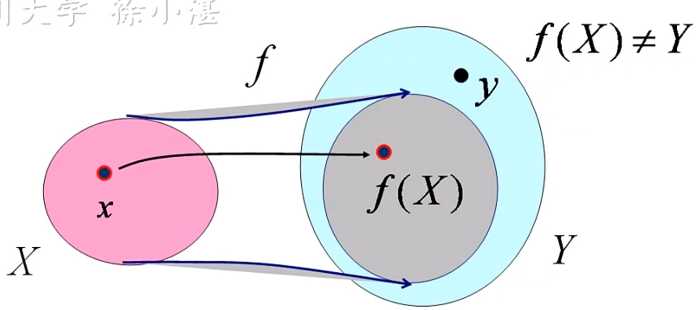
两个非空集合X与Y间存在着对应关系f,而且对于X中的每一个元素x,Y中总有有唯一的一个元素y与它对应,就这种对应称为从X到Y的映射,记作f:X→Y
y称为元素x在映射f下的象,记作:y=f(x)。x称为y关于映射f的原象。集合X中所有元素的象的集合称为映射f的值域,记作f(X)。
满射:Y中的所有元素都是映射f的象
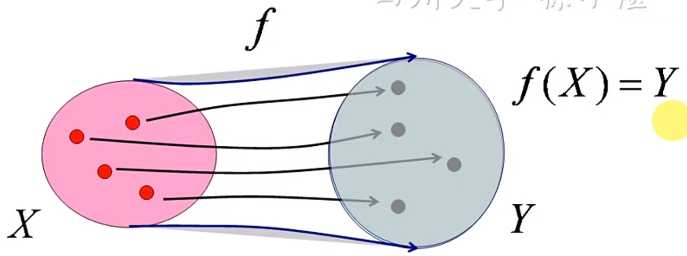
非满射:Y中的部分元素不是映射f的象
单射:X中的不同原象在Y中存在不同的象
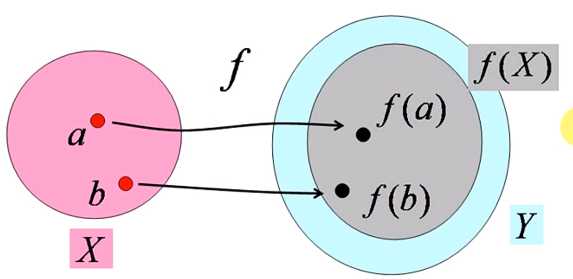
非单射:至少存在两个元素有相同的象
天子骄龙
以上是关于映射与函数的主要内容,如果未能解决你的问题,请参考以下文章