八大基本排序---堆排序堆结构

Posted 2021-11-28 yuange678

堆排序很重要，但是更重要的是堆这个结构

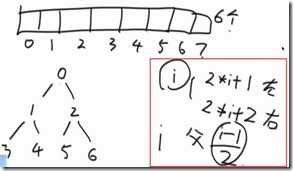
堆结构：实际上是一棵完全二叉树

一个数组可以根据父结点、左子结点、右子结点的关系，脑补出一棵完全二叉树

 

算法1：一个数组变为大顶堆 heapInsert()

数组：2、1、3、6、0、4

（1）只有2的时候

（2） 2、1【认为完全二叉树的范围是0~1的，超过1就越界】

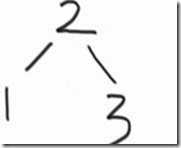
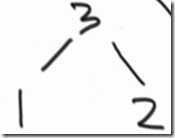
（3）2、1、3

3(下标2)找到自己的父结点：(2-1)/2=0

此时不满足大顶堆了，将2跟3交换

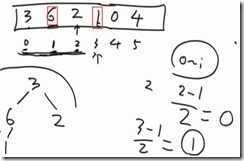
（4）2、1、3、6

6(下标3)找到它的父结点：(3-1)/2=1，发现6>1，将3位置上的数和1位置上的数交换

然后继续比较6所在的位置和它的父结点的大小

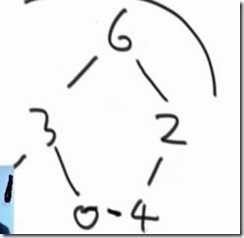
（5） 再看4位置：2、1、3、6、0

4位置的父结点是(4-1)/2=1，0(4位置)<3(1位置)，继续往下

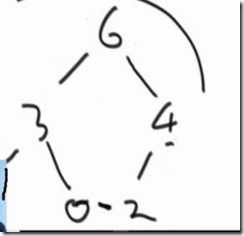
（6）再看5位置：2、1、3、6、0、4

这样每一步都会形成一个0~i的大顶堆，遍历完整个数组就形成了0~N-1的大顶堆

//一个数据插入已经是一个大顶堆的数组中，并且调整为新的大顶堆
    public static void heapInsert(int[] arr,int index) {
        while (arr[index]>arr[(index-1)/2]) {
            swap(arr, index, (index-1)/2);
            index = (index-1)/2;
        }
    }

    public static void main(String[] args) {
        int[] arr = {5,8,9,1,2} ;
        System.out.println(Arrays.toString(arr));
        for (int i = 0; i < arr.length; i++) {
            heapInsert(arr, i);
        }
        System.out.println(Arrays.toString(arr));
        
    }

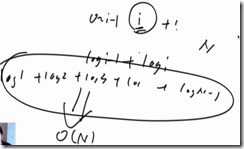
二叉树如果结点个数为N，树的高度logN，所以每加入一个结点、调整形成一个大顶堆的时间复杂度O(logN)【只需要比较自己的那个分支】

那么一个数组中一共N个结点，一个一个加入并且形成大顶堆的时间复杂度如下：

 

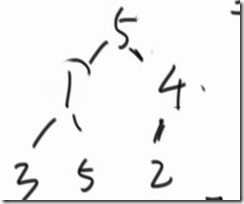
算法2：已经形成的大顶堆里有一个数字突然变小了，重新调整这个数组形成大顶堆 heapify()

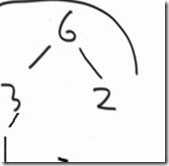
6变为1了

找到这个结点的左子结点、右子结点

左右两个结点之间先PK一下找到最大值

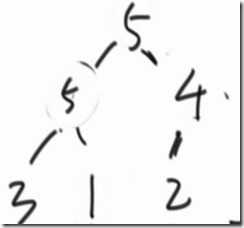
看左右两个结点之间的最大值比不比1大

1和5交换

再找1位置的左右孩子，找到一个最大值；如果没有左右孩子那就停住

 

//已经形成的大顶堆里，某一个数字(index位置的值)突然变小了，重新调整为一个大顶堆
    public static void heapify(int[] arr,int index, int heapSize){
        int left = 2*index+1;
        int largest;
        //如果当前结点的左子结点越界了，证明当前结点已经是叶结点了
        while (left<heapSize) {
            //找出左右孩子中的最大值的下标---largest
            //如果右子结点存在，那么取左右结点中的最大值；
            //如果右子结点不存在，那么取左结点就是唯一的最大值
            if (left+1<heapSize && arr[left]<arr[left+1]) {
                largest = left+1;
            }else {
                largest = left;
            }
            //父结点大于等于左右子结点中的最大值，不用动  
            if (arr[index]>=arr[largest]) {
                break;
            }else {
                swap(arr, largest, index);
                index = largest;
                left = 2*index+1;
            }
        }
    }

堆排序：

（1）先把数组调整为大顶堆

（2）把堆顶元素和最后一个位置的元素做交换

这事最大的数字换到了最后，然后让堆的大小-1（heapSize--），6就相当于永远不动了

然后从0位置开始做heapify()的调整；重新调整为大根堆

-----------------à

然后再把这个堆顶元素与堆中最后一个元素交换

import java.util.Arrays;

public class HeapSort {

    public static void main(String[] args) {
        int[] arr = {5,8,9,1,2} ;
        System.out.println(Arrays.toString(arr));
        heapSort(arr);
        System.out.println(Arrays.toString(arr));
        
    }
    
    public static void heapSort(int[] arr) {
        //1.形成大顶堆
        for (int i=0; i<arr.length; i++) {
            heapInsert(arr, i);
        }
        //2.堆顶元素跟最后一个数据交换位置，堆的大小-1
        int heapSize = arr.length;
        while (heapSize>0) {
            //恢复成大顶堆
            swap(arr, 0, --heapSize);
            heapify(arr, 0, heapSize);
        }
    }

    //之前已经是一个大顶堆了，将arr[index]加入后，调整为新的大顶堆
    public static void heapInsert(int[] arr,int index){
        //找到父结点，与父结点的值比较
        while (arr[index] > arr[(index-1)/2]) {
            swap(arr, (index-1)/2, index);
            index = (index-1)/2;
        }
    }
    
    //已经形成的大顶堆里，某一个数字(index位置的值)突然变小了，重新调整为一个大顶堆
    public static void heapify(int[] arr,int index, int heapSize){
        int left = 2*index+1;
        int largest;
        //如果当前结点的左子结点越界了，证明当前结点已经是叶结点了
        while (left<heapSize) {
            //找出左右孩子中的最大值的下标---largest
            //如果右子结点存在，那么取左右结点中的最大值；如果右子结点不存在，那么取左结点就是唯一的最大值
            if (left+1<heapSize && arr[left]<arr[left+1]) {
                largest = left+1;
            }else {
                largest = left;
            }
            //父结点大于等于左右子结点中的最大值，不用动  
            if (arr[index]>=arr[largest]) {
                break;
            }else {
                swap(arr, largest, index);
                index = largest;
                left = 2*index+1;
            }
        }
    }
    
    public static void swap(int[] arr,int i,int j){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}