八大内部排序算法之希尔堆排序插入排序算法

Posted 2021-09-06 踩踩踩从踩

前言

我们所知的八大内部的排序算法有冒泡排序、选择排序、快速排序、归并排序、链式基数排序、插入排序、希尔排序、堆排序、而这篇文章主要研究这其中的希尔排序和堆排序算法，之前的排序算法都在下面连接中介绍过，因此不在过多的赘述

线性表之顺序存储结构与链式存储结构 及 应用

五大经典算法-分治法 及其应用二分查找 、快速排序、递归排序

插入排序

插入排序顾名思义直接插入，打掉一个放一个在放数据时，直接进行排序，这样一描述是不是对于小数据量的数据排序效率还是很高的

• 首先拿出一个进行比较排序

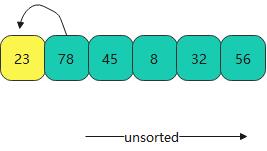
•  进行比较出来得到前两个顺序的值

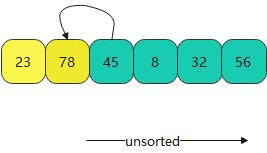
•  到第三轮时，45插入的点就在23前面

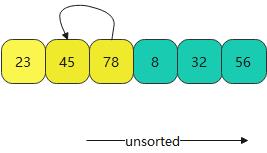
•  最后不断得到下面排序好的数据，这就是插入排序算法

这并不是一种数据交换的思维，而是直接插入移动数据的思想

代码实现

• 首先创建一个无序的数组

int[] array=new int[]{2,3,4,5,6,7,1,8,9};

• 从1开始只要 当前的点小于0，则赋值给当前值，然后 是不断插入的

int j=1;  
int target=array[j];
            while(j>0 && target<array[j-1]){
                array[j]=array[j-1];//
                j--;//这个地方是不断往遍历的，如果是1 则跳出去
            }
            array[j]=target;//如果1上的数据比0上的数据小，那这里的j已经变成了 0了，才插入

• 然后遍历所有的就是整个插入排序了

 for (int i = 1; i < array.length; i++) {
            int j=i;
            int target=array[j];
            while(j>0 && target<array[j-1]){
                array[j]=array[j-1];
                j--;
            }
            array[j]=target;
        }

这就是整个插入排序，是比较简单的，总的来说，只要比当前值小，就往后移动，然后直到移动完了，在放到插入的地方。这和冒泡排序算法和快速排序是两种思想，不要弄混了

希尔排序

运用在一些大量重复排序，自身有很多都是有序，然后采用该算法的话，效率是相当的高的

核心思想

取一个定长的值比如6，也就是固定长度数据之间进行使用插入排序进行排序好，直到全部固定长度数据进行排序，经过一轮；大部分数据就排序好了；然后继续定值去调整，  如果其中完成插入一次的操作，我们就可以完成了，就相当于排序成功了；如果固定长度取得好，可以减少非常多排序动作。

已知的最好步长序列由Marcin Ciura设计（1，4，10，23，57，132，301，701，1750，…）
 这项研究也表明“比较在希尔排序中是最主要的操作，而不是交换。” 用这样步长序列的希尔排序比插入排序和堆排序都要快，甚至在小数组中比快速排序还快， 但是在涉及大量数据时希尔排序还是比快速排序慢。

 

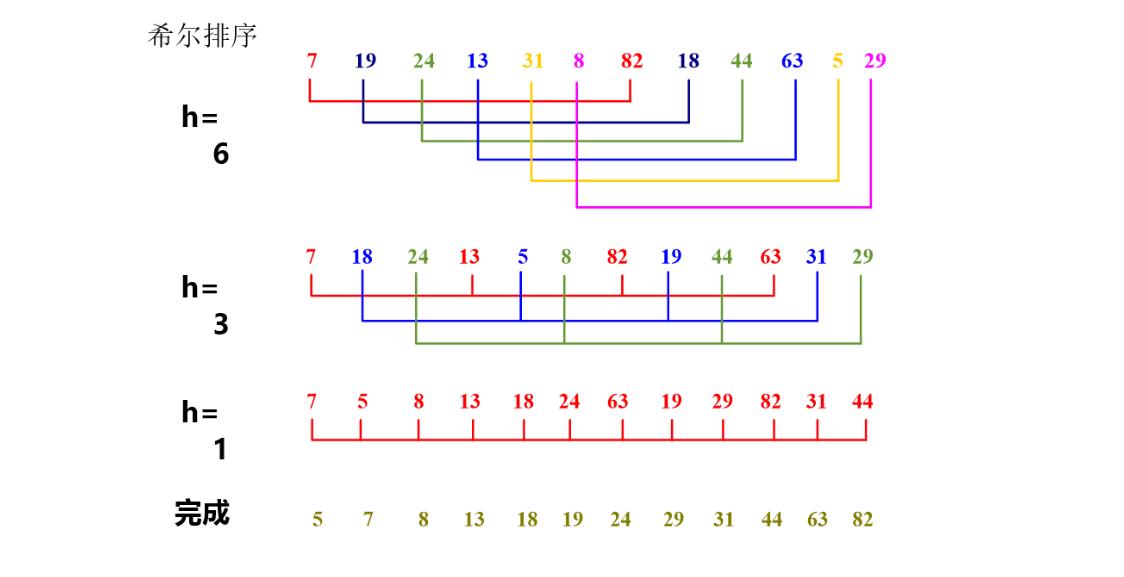
 很多数据已经排序好了数据，其他算法都会有很多不必要得逻辑运算。

代码实现

主要是在插入排序上进行改进，首先将插入排序进行复制过来

  for (int i = 1; i < array.length; i++) {
            int j=i;
            int target=array[j];
            while(j>0 && target<array[j-1]){
                array[j]=array[j-1];
                j--;
            }
            array[j]=target;
        }

• 然后进行改造，首先固定长度为3进行排序。

  //直接插入排序 step 为固定长度进行排序
            for (int i = 0 + step; i < array.length; i = i + step) {
                int j = i;
                int target = array[j];
                while (j > step - 1 && target < array[j - step]) {
                    array[j] = array[j - step];
                    j = j - step;
                }
                array[j] = target;
            }

• 而在整合起来完整得希尔排序

  public static void shellSort(int[] array,int step){
        for(int k=0;k<step;k++) {
            //直接插入排序
            for (int i = k + step; i < array.length; i = i + step) {
                int j = i;
                int target = array[j];
                while (j > step - 1 && target < array[j - step]) {
                    array[j] = array[j - step];
                    j = j - step;
                }
                array[j] = target;
            }
        }
    }

希尔排序适合小数组进行排序，需要进行多次排序

 shellSort(array,4);
        //2 3 1 5 6 7 4 8 9
        shellSort(array,1);

• 时间复杂度是非常难确定得，根据定长值来确定的

堆排序

 堆的概念

 近似于完全二叉树的概念，也就是

leftNo = [2n+1]
rightNo = [2（n+1）]；

堆排序是什么

堆排序（英语：Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。这就是最大顶堆，而我们在PriorityQueue 优先队列中采用最小顶堆排序

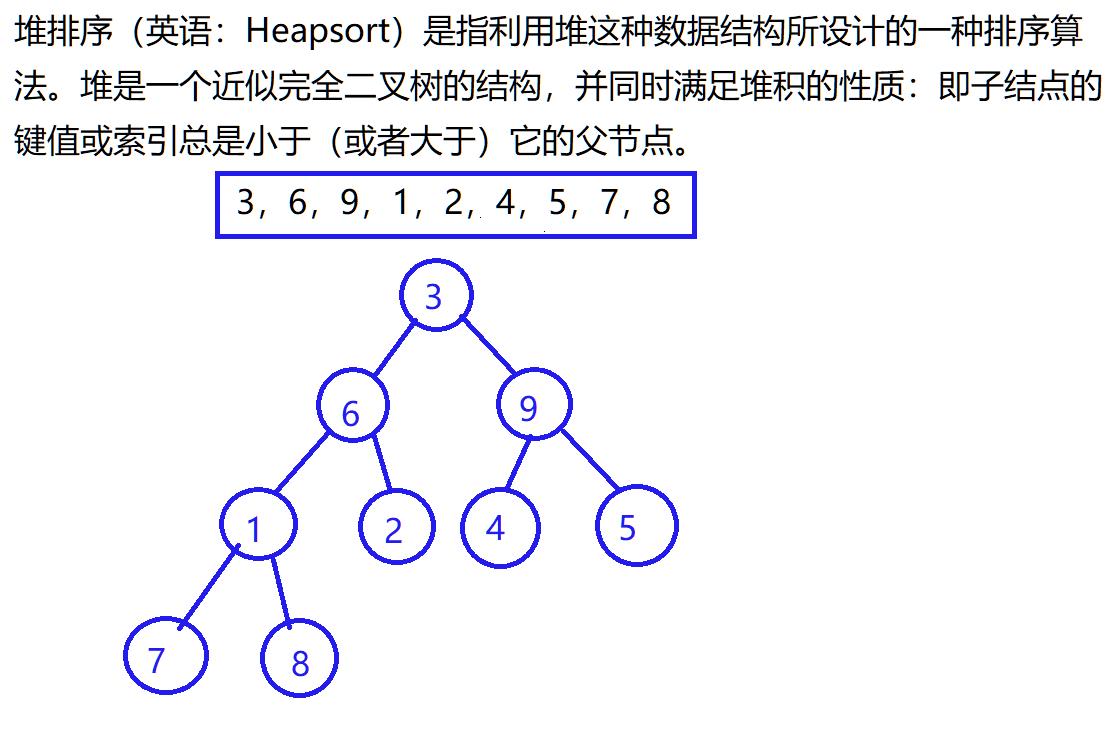
大家可以看看我分析的jdk中集合源码分析

Java 集合深入理解 （九） ：优先队列（PriorityQueue）之源码解读，及最小顶堆实现研究

我们继续分析堆排序的过程 大顶堆

• 从最后一个非叶子节点开始，每三个节点做一次大小比较，最小的做根如果移动过程中如果子树上的顺序被破坏了，子树上重新调整三个节点的位置      
• 取走整个树的根节点，把最后一个叶子做为根节点 
• 重复1和2，直到所有节点被取走了

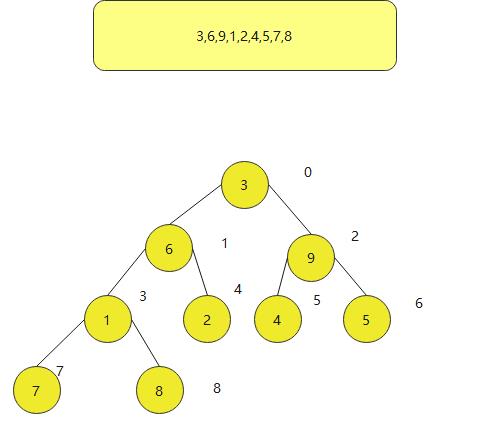
 这里怎么找到父节点和做节点和右节点

   父节点是: (n-1)/2

   左孩子是: 2*n+1

   右孩子是: 2*n+2

代码实现

• 首先创建一个调整堆的方法，并记录起始的位置 

  /**
     * 调整堆
     */
    void maxHeapify(int array[],int start,int end){
        //父亲的位置
        int dad=start;
        //儿子的位置
        int son=dad*2+1;
       
    }

• 当我们从中间进行调整时，包括子节点都有可能需要调整，如果子节点下标在可以调整的范围内就一直调整下去。

  /**
     * 调整堆
     */
    void maxHeapify(int array[],int start,int end){
        //父亲的位置
        int dad=start;
        //儿子的位置
        int son=dad*2+1;
       while(son<=end){//如果子节点下标在可以调整的范围内就一直调整下去
       
        }
       
    }

• 如果没有右孩子就不用比,有的话,比较两个儿子，选择最大的出来

  /**
     * 调整堆
     */
    void maxHeapify(int array[],int start,int end){
        //父亲的位置
        int dad=start;
        //儿子的位置
        int son=dad*2+1;
       while(son<=end){//如果子节点下标在可以调整的范围内就一直调整下去
           //如果没有右孩子就不用比,有的话,比较两个儿子，选择最大的出来
            if(son+1 <= end && array[son]<array[son+1]){
                son++;
            }
        }
       
    }

• 这里需要对进行调整

  /**
     * 调整堆
     */
    void maxHeapify(int array[],int start,int end){
        //父亲的位置
        int dad=start;
        //儿子的位置
        int son=dad*2+1;
       while(son<=end){//如果子节点下标在可以调整的范围内就一直调整下去
           //如果没有右孩子就不用比,有的话,比较两个儿子，选择最大的出来
            if(son+1 <= end && array[son]<array[son+1]){
                son++;
            }

              //和父节点比大小
            if(array[dad]>array[son]){
                return;
            }else{//父亲比儿子小，就要对整个子树进行调整
                int temp=array[son];
                array[son]=array[dad];
                array[dad]=temp;
                //递归下一层
                dad=son;
                son=dad*2+1;
            }
        }
       
    }

• 开始进行建堆

 void heapSort(int array[],int len){
//建堆  len/2-1最后一个非叶子节点
        for(int i=len/2-1;i>=0;i--){
            maxHeapify(array,i,len-1);
        }
}

•   排序,根节点和最后一个节点交换，换完以后，取走根，重新建堆，len-1 最后一个节点

 void heapSort(int array[],int len){ 
 for(int i=len-1;i>0;i--){
            int temp=array[0];
            array[0]=array[i];
            array[i]=temp;
            maxHeapify(array,0,i-1);
        }
}

• 最后完整的代码

 void heapSort(int array[],int len){
        for(int i=len/2-1;i>=0;i--){
            maxHeapify(array,i,len-1);
        }
        for(int i=len-1;i>0;i--){
            int temp=array[0];
            array[0]=array[i];
            array[i]=temp;
            maxHeapify(array,0,i-1);
        }
    }

应用场景

   在大数据情况下找到前n个数据

八大内部排序的各大应用场景

• 冒泡排序：针对8个以内的数据，速度是很快的

• 选择排序：针对8个以内的数据，速度也是很快的

• 快速排序：针对的是数据量大，并且是线性结构，但大量重复数据和链式结构不适合采用二分的思想

• 归并排序：针对大量排序方式，重复数据，链式结构，但是空间要求相当大

• 链式基数：有多关键字排序，可以考虑这种方式

• 插入排序：也是针对小数据量

• 希尔排序：针对比较多的重复数据 

• 堆排序：应用在大数据下找前n个数据

平常我们在算法的选择，根据业务场景和算法的特点来选择的。

总结

整篇文章我主要分析了各种不同排序方式的应用场景。然后 像希尔排序的核心还是在插入排序，然后冒泡和选择排序是一类的，而快排的基础是选择排序，归并和快排的核心思想来源于二分；堆排序则是来源与堆的特性 。各种排序都是有联系的。而在不同的业务场景选择不同的方法是主要思想。