用弦截法求一元三次方程的根x^3-5x^2+16x-80=0 ；带注释！

Posted 2020-07-20 海中月

//用弦截法求一元三次方程的根x^3-5x^2+16x-80=0
#include<stdio.h>
#include<math.h>
 float f(float x) //定义子函数f(x) = x^3-5x^2+16x-80，当f(x) →0时，则x即为所求的实数根；
 {
     float y;
     y=((x-5.0)*x+16.0)*x-80.0;
     return(y);          //返回f(x)的值
 }
 
  float xpoint( float x1,float x2)//定义子函数xpoint，求出弦与x轴的交点的x0值；
  {
      float x0;
      x0=(x1*f(x2)-x2*f(x1))/(f(x2)-f(x1));   //计算弦与x轴交点x0位置的值
      return(x0);                      //返回x0位置的值
  }
 
  float root(float x1,float x2) //定义子函数root，求近似实根
   {
       float x0;                 
       do      //关键循环步骤，未达到条件前一直do循环运算；
       {
         x0=xpoint(x1,x2);  //此处调用上面的子函数xpoint(x1,x2)，得到弦与x轴交点位置x0的值
         if(f(x0)*f(x1)>0)  //此处调用子函数f(x)，得到x轴x0位置的f(x0)值，得到x1位置的f(x1)值，如果f(x0)*f(x1)>0，即同符号的话；
              x1=x0;           //将x0赋值 →x1，则下次继续循环运算的区间为x0(x1)－x2
      else              //否则，如果f(x0)*f(x1)<0，即异号的话；
           x2=x0;          //将x0赋值 →x2 ，则下次继续循环运算的区间为x1－x0(x2)
       }
       while(fabs(f(x0))>=1e-6);//当型循环判断条件，1e-6为取值精度，f(x0)接近于0，即接近于x轴相交，如运算无结果可能循环次数太多，可减少幂的次数再试。
       return(x0);         //返回x0位置的值
   }
    
    main() //主函数
{
    float x1,x2,x0;
    do
    {
     printf("请输入预估的实根区间的两个数值x1,x2:\\n");
     scanf("%f,%f",&x1,&x2); //输入两个数x1,x2
     }
     while (f(x1)*f(x2)==0);//当循环运算到f(x1)*f(x2)>=0时(0是必要条件参数)，即f(x1)、f(x2)同符号，且任一个接近于0时，意味着与x轴接近相交，此时存在一个方程实根。
     x0=root(x1,x2);        //此处x0即为方程实根；
     printf("其中的一个方程实根为：%.4f",x0);
 }
 

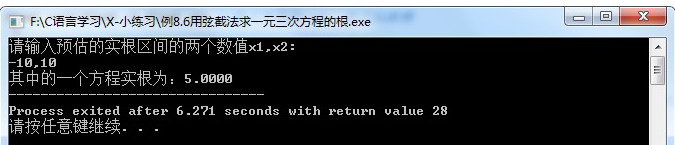
举个例子：x1=-10,x2=10,运算结果为：