python怎么求解一元二次方程的根?

Posted 2023-05-07

import numpy as np

def solve_quad(a,b,c):

if a == 0:

print('您输入的不是二次方程!')

else:

delta = b*b-4*a*c

x = -b/(2*a)

if delta == 0:

print('方程有惟一解，X=%f'%(x))

return x

elif delta > 0:

x1 = x-np.sqrt(delta)/(2*a)

x2 = x+np.sqrt(delta)/(2*a)

print('方程有两个实根:X1=%f,X2=%f'%(x1,x2))

return x1,x2

else:

x1 = (-b+complex(0,1)*np.sqrt((-1)*delta))/(2*a)

x2 = (-b-complex(0,1)*np.sqrt((-1)*delta))/(2*a)

print(x1,x2)

return x1,x2

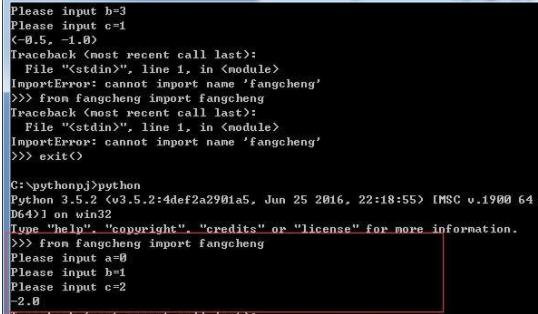
Python

是完全面向对象的语言。函数、模块、数字、字符串都是对象。并且完全支持继承、重载、派生、多继承，有益于增强源代码的复用性。Python支持重载运算符和动态类型。相对于Lisp这种传统的函数式编程语言，Python对函数式设计只提供了有限的支持。有两个标准库(functools, itertools)提供了Haskell和Standard ML中久经考验的函数式程序设计工具。

参考技术A 你可以得到最简单的代码求解
import math

a = 1
b = -90
c = 2025

delta=b ** 2 - 4 * a * c

print((-b + math.sqrt(delta)) / (2 * a))
print((-b - math.sqrt(delta)) / (2 * a))
可以用编辑器，交互环境不知道能不能用

112.求解非线性方程

#include "math.h"
#include "stdio.h"


int BinSearchRoot(a,b,h,eps,x,m) /*用二法计算非线性方程的实根*/
int m;
/*参数意义：
a    要求的根的下界
b    要求的根的上界，即：所求的根落在区间 [a,b]之内
h    递进的步长
eps  精度
x    根的值
m    预计的根的个数*/
double a,b,h,eps,x[];
 
	extern double Equation(); /*要求解的非线性方程*/
    int n,js;
    double z,y,z1,y1,z0,y0;
    n=0; z=a; y=Equation(z);
    while ((z<=b+h/2.0)&&(n!=m)) /*对给定步长的子区间进行搜索*/
	 
		if (fabs(y)<eps)  /*当前的判定点是方程的根*/
		 
			n=n+1; 
			x[n-1]=z;
            z=z+h/2.0; 
            y=Equation(z);
		
        else /*当前点不是方程的根*/
		 
			z1=z+h; 
			y1=Equation(z1);
			if (fabs(y1)<eps) /*下一个点是方程的根*/
			 
				n=n+1;
				x[n-1]=z1;
				z=z1+h/2.0;
				y=Equation(z);
			
			else if (y*y1>0.0) /*该区间内无根*/
			 y=y1; z=z1;
			else   /*该区间内有根*/
			 
				js=0;/*标志，0表示未找到根，1表示已经确定了根*/
				while (js==0)
				 
					if (fabs(z1-z)<eps) /*区间的长度小于给定的精度，可以当作已经找到了根*/
					 
						n=n+1;  
						x[n-1]=(z1+z)/2.0; /*把区间的中位值作为根*/
						z=z1+h/2.0; /*把寻找的位置放到下一个区间内*/
						y=Equation(z);
						js=1; /*在当前区间内已经找到了根*/
					
					else /*区间比给定的精度大，则进行二分*/
					 
						z0=(z1+z)/2.0;  /*区间二分*/ 
						y0=Equation(z0);
						if (fabs(y0)<eps) /*z0位置为根*/
						 
							x[n]=z0; 
							n=n+1; 
							js=1;
							z=z0+h/2.0; 
							y=Equation(z);
						
						else if ((y*y0)<0.0) /*[z,z0]内有根*/
						 z1=z0; y1=y0; 
						else  z=z0; y=y0;
					
				
			
		
	
    return(n); /*返回根的个数*/

main()

	int i,n;
    static int m=6;
    static double x[6];
    clrscr();
    puts("This is a program to solve Nonlinear function\\n   by Binary Divisive Procedure.");
    puts("\\n The Nonlinear function is:");
    puts("\\n f(x)=(((((x-5.0)*x+3.0)*x+1.0)*x-7.0)*x+7.0)*x-20.0\\n");
    n=BinSearchRoot(-2.0,5.0,0.2,0.000001,x,m);
    puts("\\n >> Solve successfully!\\n >> The results are:");
    printf(" >> The function has %d roots, they are:\\n",n);/*输出根的个数*/
    for (i=0; i<=n-1; i++)
		printf(" >> x(%d)=%13.7e\\n",i,x[i]);
    printf("\\n Press any key to quit...\\n");
    getch();



double Equation(x)
double x;

	double z;
	z=(((((x-5.0)*x+3.0)*x+1.0)*x-7.0)*x+7.0)*x-20.0;
	return(z);