[从头学数学] 第228节 函数与极限

Posted 2020-07-16 mwsister

剧情提要：
[机器小伟]在[工程师阿伟]的陪同下进入了元婴期的修炼。
这次要修炼的是数学分析（或称高等数学、或称微积分）。

正剧开始：

星历2016年05月28日 17:08:16, 银河系厄尔斯星球中华帝国江南行省。
[工程师阿伟]正在和[机器小伟]一起研究[函数与极限]。

<span style="font-size:18px;">###
# @usage   集合、函数映射
# @author  mw
# @date    2016年05月28日  星期六  13:14:05 
# @param
# @return
#
###


#集合、函数映射
class FunctionMap():
    def __init__(self):
        self._Expr = alg.AlgExpressionCalc();

    #把一个数组封装成一个字符串， 如=>[(3)*x^[1],(3)*y^[1],(1)*x^[2]]
    #由于使用目的单一，这个数组代表的是多项式
    #所以，必然只是一维的数组 
    def zipArray2String(self, array):
        s = '[';
        for i in range(len(array)):
            s+='\\''+array[i]+'\\',';
        #去除最后的加号
        s = s[:-1];
        s += ']';
        return s;

    
    #把一个表示数组的字符串拆分成数组
    #注意：这个字符串必然是由格式化后的数组封装成的
    #不要把任意字符串拿来处理，会出错的
    def zipString2Array(self, s):
        s = s.replace('\\'', '');
        #去除最外面的[]对
        s = s[1:-1];
        array = [];
        #记录加号的位置，这个加号必然后面紧跟一个(号，这是格式
        signIndex = s.find(',');
        if signIndex == -1: #原数组只有一个单项式
            pass;
        else:
            while (signIndex != -1):
                array.append(s[:signIndex]);
                s = s[signIndex+1:];
                signIndex = s.find(',');
            
        array.append(s);

        return array;

    #把一个字符串中的所有空格去除
    def removeSpaceInString(self, str1):
        return str1.replace(' ', '');
    
    #把一个字符串中的所有小括号的位置按层次返回一个标示数组
    #如'((0))(0)' = [-1, -2, 0, 2,1, -1, 0, 1];
    def bracketLevelIndexArray(self, str1):
        len_ = len(str1);
        array = [0]*len_;

        #初始化左、右括号为0级，遇左括号-1，遇右括号+1
        lLevel = rLevel = 0;

        for i in range(len_):
            if (str1[i] == '('):
                lLevel-=1;
                array[i] = lLevel;
            elif (str1[i] == ')'):
                rLevel = -lLevel;
                array[i] = rLevel;
                lLevel+=1;

        #左右括号匹配检查
        if abs(min(array)) != abs(max(array)):
            print('左右括号不匹配！');
            #括号不匹配，默认没有括号，这里可以作为函数式是否需要求解的一个判定
            #因为如果没有括号，可以认为没有函数映射
            return [0]*len_;

        return array;
            

    #输入函数和自表量[[名称，值代数式]...]的映射表，返回值代数式（可解）
    #或原样输出函数和自表量[[名称，值代数式]...]的映射表（不可解时）
    def functionMapCalc(self, fun, variableMap):
        #去掉多余的空格，这是格式化的一部分
        fun = self.removeSpaceInString(fun);
        #判断是否可计算
        if (not self.judgeEvalable(fun)):
            return [fun, variableMap];
        
        bracketArray = self.bracketLevelIndexArray(fun);
        maxBracketLevel = max(bracketArray);

        #没有括号，表示没有函数映射的存在，直接返回输入值
        if (maxBracketLevel <= 0):
            return [fun, variableMap];

        #到这里就确定函数可以计算了
        #每次取最里面的括号部分进行计算


        #把函数中的每个右括号都多加一层，这样是给'self._Expr.strPolyCombine('调用对上        
        funChanged = fun.replace(')', '))');

        for i in range(len(variableMap)):
            #映射表中的参数名称
            var = variableMap[i][0];
            #前后加限定防止过度匹配
            sL = '('+var+',';
            sR = ','+var+')';

            varValue = self.zipArray2String(variableMap[i][1]);
            funChanged = funChanged.replace(sL, '('+varValue+',');
            funChanged = funChanged.replace(sR, ','+varValue+')');

        #每一步操作后都后并一下同类项
        sFun = 'self._Expr.strPolyCombine(';

        #幂， 乘， 加， 减， 负
        sPow = 'self._Expr.strpow_n';
        sMul = 'self._Expr.strdot';
        sAdd = 'self._Expr.stradd';
        sSub = 'self._Expr.strsub';
        sMinus = 'self._Expr.strminus';
        
        
        funChanged = funChanged.replace('[POW]', sFun+sPow);
        funChanged = funChanged.replace('[MUL]', sFun+sMul);
        funChanged = funChanged.replace('[ADD]', sFun+sAdd);
        funChanged = funChanged.replace('[SUB]', sFun+sSub);
        funChanged = funChanged.replace('[MINUS]', sFun+sMinus);

        return [eval(funChanged), variableMap];        


    #判断关于多项式的函数式可否计算得出多项式解
    #只要含有下面所列函数，则认为不可以得出多项式解
    #这时的处理就会将原函数依样返回
    def judgeEvalable(self, fun):
        if (fun.find('[DIV]') != -1 or
            fun.find('[LOG]') != -1 or
            fun.find('[LN]') != -1 or
            fun.find('[EXP]') != -1 or
            fun.find('[SIN]') != -1 or
            fun.find('[COS]') != -1 or
            fun.find('[TAN]') != -1 or
            fun.find('[ASIN]') != -1 or
            fun.find('[ACOS]') != -1 or
            fun.find('[ATAN]') != -1):
            return False;

        return True;

def tmp():
    #代数式
    Expr = alg.AlgExpressionCalc();
    #函数映射
    Map = FunctionMap();

    #多项式拆装实验
    a = Expr.strPolyCombine(Expr.strPolyFormat(['x', 'y', '2x', '2y', 'x^[2]']));    
    print(a);

    s = Map.zipArray2String(a);
    print(s);

    a = Map.zipString2Array(s);
    print(a);

    b = Expr.strPolyFormat(['x']);
    c = Expr.strPolyFormat(['2']);
    print(b);
    print(c);
    #函数映射的格式化写法：[函数名](自变量多项式)
    fun = Map.removeSpaceInString('[MUL]([MUL]([POW](a, 2), b), c)');

    calc = Map.functionMapCalc(fun, [['a', a], ['b', b], ['c', c]]);
    print(calc);</span>

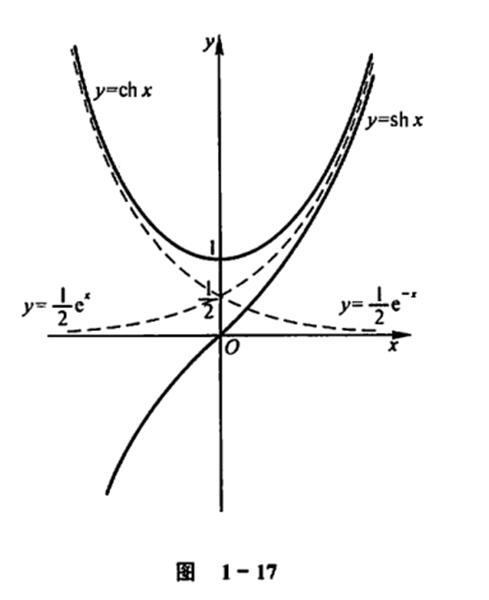
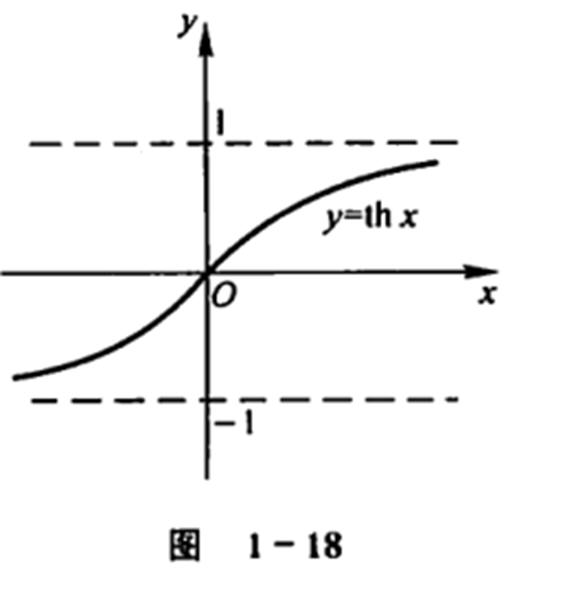
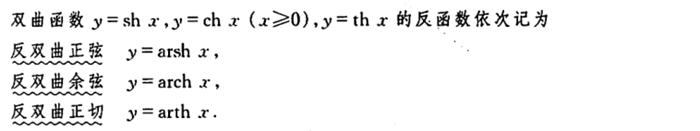
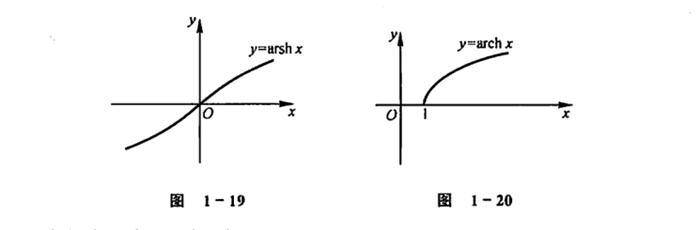
本节到此结束，欲知后事如何，请看下回分解。