Java 实现任意N阶幻方的构造

Posted 2020-07-15 CuriousZero

一、关于单偶数阶幻方和双偶数阶幻方

（一）单偶数阶幻方（即当n=4k+2时）

  　　任何4k+2 阶幻方都可由2k+1阶幻方与2×2方块复合而成，6是此类型的最小阶。

  　　以6阶为例，可由3阶幻方与由0,1,2,3组成的2×2的小方块拼成一个6×6的大方块复合而成。

       其中，3阶幻方（洛书）如下图1所示，

      

    （图1）

 将每一单元格分成4等块，各小块的值与单元格的值相同，则行和、列和、对角和均为30，（见图2），记为方阵M

（图2）

用由0,1,2,3组成的2×2的小方块拼成一个6×6的大方块，使其行和、列和、对角和均为9，记为方阵N，（见图3）

（图3）

故6阶幻方为方阵4M-N（见图4）

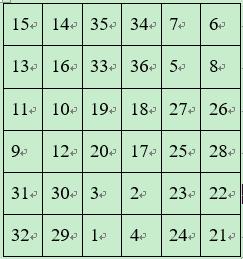
（图4）

流程图为：

（二）双偶数阶幻方（即当n=4k时）

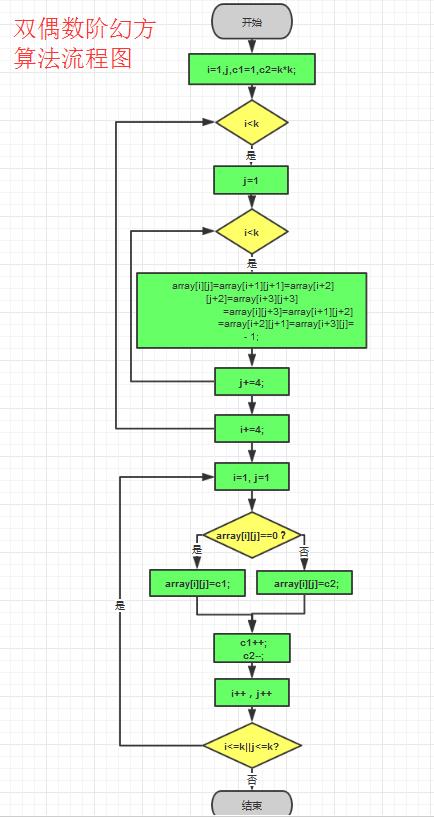
如上图所示，数字可分为有圈型和无圈型。对任意的4k阶幻方，可将其等分为k*k个如上图所示的4×4元组的结构。例如8阶幻方可分成4个上述结构，无圈的按照“自左至右、自上至下”的顺序把1~64个数填上，有圈的先放空；有圈的按照“自右至左，自下至上”的顺序把1~64个数填上，无圈处暂放空。这样即可生成8阶幻方。

流程图为：

二、具体代码

package MagicSquare;

import java.util.Scanner;

import javax.sql.rowset.FilteredRowSet;

public class MagicSquare {
    
    
    //奇数幻方的实现:
    //卢培步法求奇数阶幻方的函数，参数依次是储存幻方的数组的名称、幻方的阶数，
    //标志位flag(为1表示主函数直接调用求奇数阶幻方，为0表示SingleEven_Magic函数进行的调用)
    public static void  Odd_Magic(int array[][],int k ,int flag){
        int i=k,j=(k+1)/2,c=1;
        while (c<=k*k) {
            array[i][j]=c;
            if (c%k==0) {//若c是k的倍数，向上走
                i-=1;
            }
            else{//若c不是k的倍数，向右下走
                i+=1;
                j+=1;
                if (i>k) {
                    i=1;
                }
                if (j>k) {
                    j=1;
                }
            }
            c++;
        }
        if (flag==1) {
            outputArray(array);
        }
    }
    
    //双偶数幻方：
    //即：阶数能够被4整除的幻方构造函数，参数依次是储存幻方的数组的名称、幻方的阶数
    public static void  DoubleEven_Magic(int array[][],int k) {
        int i=1,j,c1=1,c2=k*k;
        while (i<k) {  //把4k阶看作k*k 个4*4 的方块，将主对角线和反对角线上的元素标记为 -1
            j=1;
            while (j<k) {
                array[i][j]=array[i+1][j+1]=array[i+2][j+2]=array[i+3][j+3]
                        =array[i][j+3]=array[i+1][j+2]
                        =array[i+2][j+1]=array[i+3][j]= - 1;
                j+=4;
            }
            i+=4;
        }
        
        for(i=1;i<=k;i++)
            for(j=1;j<=k;j++){
                
                //标记为0的进行正向依次赋值（java 在整型数组实例化时将所有元素初始化赋值为0）
                if (array[i][j]==0) {
                    array[i][j]=c1;
                }
                //否则，标记为-1 的进行反向依次赋值。
                else{
                    array[i][j]=c2;
                }
                c1++;
                c2--;
            }
            outputArray(array);//输出幻方
        
    }
    
    
    //单偶数幻方：
      //即：阶数被4除余2的幻方构造函数，参数依次是储存幻方的数组的名称、幻方的阶数
    public static void  SingleEven_Magic(int array[][],int k) {
        int a[][]=new int[k+1][k+1];
        int b[][]=new int [k+1][k+1];
        int m[][]=new int [k/2+1][k/2+1];
        int i,j;
        
        Odd_Magic(m, k/2, 0);
        
        //由k/2奇数阶幻方衍生出1比4的k阶方阵M
        for(i=1;i<=k/2;i++)
            for(j=1;j<=k/2;j++){
                a[2*i-1][2*j-1]=a[2*i-1][2*j]=a[2*i][2*j-1]=a[2*i][2*j]=m[i][j];
            }
        
        //构造方阵N
        i=1;j=1;
        while (i<k) {
            j=1;
            while (j<k) {
                //上半部分A型 1230
                if (i<k/2||i==k/2&&(j==k/2+2||j==k/2-2)||i==k/2+2&&j==k/2) {
                    b[i][j]=1;
                    b[i][j+1]=2;
                    b[i+1][j]=3;
                    b[i+1][j+1]=0;
                }
                //左半部分C型 3102
                else if(i==k/2&&j<k/2-2){
                    b[i][j]=3;
                    b[i][j+1]=1;
                    b[i+1][j]=0;
                    b[i+1][j+1]=2;
                }
                //右半部分D型 2013
                else if(i==k/2&&j>k/2+2){
                    b[i][j]=2;
                    b[i][j+1]=0;
                    b[i+1][j]=1;
                    b[i+1][j+1]=3;
                }
                //6*6 核心中央和两足 1203
                else if(i==k/2&&j==k/2||i==k/2+2&&(j==k/2+2||j==k/2-2)){
                    b[i][j]=1;
                    b[i][j+1]=2;
                    b[i+1][j]=0;
                    b[i+1][j+1]=3;
                }
                //下半部分B型 2103
                else {
                    b[i][j]=2;
                    b[i][j+1]=1;
                    b[i+1][j]=0;
                    b[i+1][j+1]=3;
                }
                j+=2;
            }
            i+=2;    
        }
        
        for(i=1;j<=k;i++)
        for(j=1;j<=k;j++){
            array[i][j]=4*a[i][j]-b[i][j];  //4*M-N 幻方形式
        }
        //outputArray(array);
        System.out.println();
        //两种幻方输出时中间间隔一行；
        for(i=1;i<=k;i++)
        for(j=1;j<=k;j++){
            array[i][j]=a[i][j]+(k/2)*(k/2)*b[i][j];   //M+(k/2)*(k/2)*N 幻方形式
           
        }
         outputArray(array);
    }
    
    //输出幻方的函数，参数是储存幻方的数组的名称
    public static void outputArray (int array[][]) {
        for(int row=1;row<array.length;row++){
            for (int column = 1; column < array[row].length; column++) {
                System.out.printf("%5d",array[row][column]);
            }
            System.out.println();
        }
    }
    
    
    
    //测试函数
    public static void  main(String args[]) {
        int a[][];
        System.out.println("请输入幻方阶数：");
        Scanner input =new Scanner(System.in);
        int k=input.nextInt();
        a=new int[k+1][k+1];
        
        //阶数为2的幻方不存在
        if (k==2) {
            System.out.println("不存在阶数为2的幻方，请重新输入！");
        }
        //奇数阶幻方
        else if (k%2!=0) {
            Odd_Magic(a, k, 1);
        }
        //4k型幻方（双偶数幻方）
        else if (k%4==0) {
            DoubleEven_Magic(a, k);
        }
        //4k+2型幻方（单偶数幻方）
        else {
            SingleEven_Magic(a, k);
        }
    }
}

 

三、结果截图

 

 

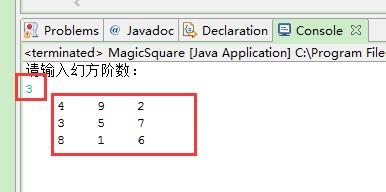
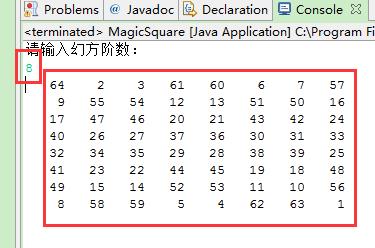
（相关源码详见：https://github.com/shenxiaolinZERO/Resources/tree/master/Resources/Magic_Test）

 

 

将每一单元格分成4等块，各小块的值与单元格的值相同，则行和、列和、对角和均为30，（见图2），记为方阵M