科普入门概率与分布密度 贝叶斯理论入门 数据挖掘基础入门
Posted pythonlearner
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了科普入门概率与分布密度 贝叶斯理论入门 数据挖掘基础入门相关的知识,希望对你有一定的参考价值。
概率Probability,先验概率Prior,后验概率Posterior
- 概率是一个衡量不确定性的工具。
一个例子:我们来估测某一个人的生日是十月份的概率,在没有任何数据样本的情况下,我们可以估计这个概率是(Pr(October) = frac{1}{12}approx8.3%).
现在假设我们有了几万个样本,通过统计这几万个样本的生日月份,绘制出数据分布图:

然后通过计算,根据这个数据样本,发现总共有7%的人的生日是十月份的,这就与没有数据的8.3%的估计不同了。(Pr(October|D)=7\%)。
- 这里的先验概率Prior,就是没有数据样本时候的估计概率,就是8.3%;
- 后验概率Posterior,就是有了数据样本的估计概率7%。
概率分布
- 概率分布就是probability distribution
- 如果这个随机变量X是离散的,就是像上面的例子一样,一月二月三月这样离散的,那么就叫做概率分布probability distribution
- 如果这个随机变量X是一个连续变量,那么就叫做概率密度分布probability density function
累积分布函数CDF
- Cumulative distribution function累积分布函数
- 按照上面生日的例子来说,累积分布函数就是前面概率的累加,(Pr(Xleq October)),就是这个人的出生的月份在1月到10月之间的概率,就是把概率分布累加起来了。
多元随机变量Multivariate Random Variable
- 对于多元随机变量,概率分布就叫做联合概率分布joint distribution。如果多元随机变量是连续的,那么就是联合概率密度分布Joint density distribution.
独立independent
对于多元随机变量而言,随机变量之间是要考虑是否独立。两个变量之间没有关系,就是独立。
- If there is no relationship between two random variables, they are called independent.

- 条件独立conditionally independent就是给定一个条件Z,X和Y才是独立的。
这里注意几个概念:
- Correlation和relationship不一样,relationship一般就是指是否独立independence。
- Correlation是指两个变量之间的相关性,与独立没有必然联系。
- 因果性causaation,一般也是指relationship和independence。
- Correlation可能存在,但是因果性不存在;correlation可能不存在,但是因果性存在,两者之间不存在必然关系。但是一般来说因果性存在,那么correlation应该是存在。
模型与样本

从数据挖掘的角度来说,我们并不是用线性回归、神经网络这些模型去拟合样本。上图中的MODEL不是指线性归回这些的模型,而是一种更加本质的东西,是万物运行的机理。我们这些样本就是从这万物机理中获得到的观测数据,我们无法直接获得到这个本质的机理,所以只能通过观测获取样本,然后用样本训练模型去拟合这个本质的机理。
每一个本质都看作一个概率密度,每一个样本其实可以看做从本质中的采样。样本通过概率从本质中进行采样,然后通过样本的数据描述Statistical inference来对本质进行描述。而这个Statistical inference就是我们使用的线性回归,贝叶斯理论,神经网络这些模型。
贝叶斯理论Bayes theorem
考虑上面的例子,想要判断一个人的生日是那个月份。我们提出了一个假设,假设这个人的生日是十月份的,如何验证这个假设呢?
- 通常我们使用贝叶斯理论Bayes theorem去验证一个假设,再给出一个数据库的情况下。
- 假设假设这个人的生日是十月份的用( heta)来表示,
- 所以之前提到的先验概率Prior:(Pr( heta)=frac{1}{12}approx8.3%)
- 后验概率Posterior:(Pr( heta|D)=7\%),就是给出了数据库的概率。
- 似然Likelihood:(Pr(D| heta)),就是后验概率的反过来的概率。
- 贝叶斯理论就是将上面三个概率结合起来:(Pr( heta|D)=frac{Pr(D| heta)*Pr( heta)}{Pr(D)})
按照上面的例子,这个人的生日的月份,我们给出的答案应该是(Pr( heta|D))最大的那个假设,(Pr(October|D)=7\%),所以生日是十月份的概率是7%。所以我们可以得到下面的公式,一般也叫做天真贝叶斯分类器:
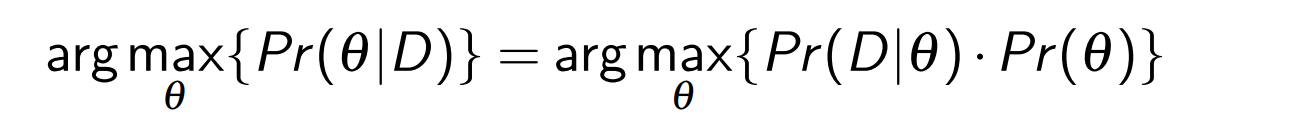
以上是关于科普入门概率与分布密度 贝叶斯理论入门 数据挖掘基础入门的主要内容,如果未能解决你的问题,请参考以下文章