区间dp

Posted 2020-11-30 s-gloria

后来我是发现还是区间dp最简单QwQ..

在区间dp中，一个状态由若干个比它小且包含它的区间所代表的状态转移而来，初态一般就由长度为1的‘元区间’构成。　——lyd《算法竞赛进阶指南》

 

 

大概就是将原本很长的一段区间不断细化，直到成为一个元区间可以求解为止。

 

举个栗子：

 

石子合并题目做了无数遍了，题意就不再赘余。

 

之前觉得它不太好理解，现在想来，不过就是一个区间不断分分分，直到成为两段相邻元区间。

see 图...

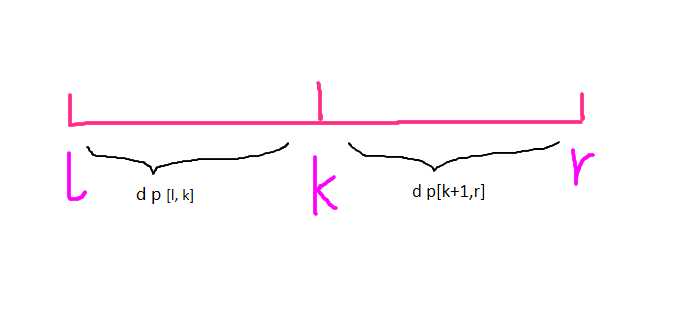
最后总会剩下两堆石子进行合并，那么就可以得到动态转移方程：

f[l,r]=max(f[l,r],f[l,k]+f[k+1,r]+合并代价）

初值：f[l][l]=A_l

目标：f[1][n]

合并代价怎么算呢，前缀和啊，说到这里应该很透彻了叭QwQ

 

 那么问题来了，这可是一堆石子围成了个圈a，这可怎么办呢？

还是啊，因为不知道从哪断开才是最合理的，于是就枚举啊，把一个圈拆开，拆成2n长度不就可以了，长度又不会变。

 1 #include<iostream>
 2 #define maxn 500
 3 using namespace std;
 4 int num[maxn],a[maxn];
 5 int dp1[maxn][maxn],dp2[maxn][maxn];
 6 int main()
 7 {
 8     int n;
 9     cin>>n;
10     for(int i=1;i<=n;i++)
11     {
12         cin>>a[i];
13         num[i]=num[i-1]+a[i];
14     }
15     for(int i=n+1;i<=2*n;i++)
16         num[i]=num[i-1]+a[i-n];
17     for(int ll=1;ll<n;ll++)
18     {
19         for(int i=1;i<2*n;i++)
20         {
21             int j=i+ll;
22             if(j<2*n)
23             {
24                 dp2[i][j]=9999999;
25                 for(int k=i;k<j;k++)
26                 {
27                     dp1[i][j]=max(dp1[i][j],dp1[i][k]+dp1[k+1][j]+num[j]-num[i-1]);
28                     dp2[i][j]=min(dp2[i][j],dp2[i][k]+dp2[k+1][j]+num[j]-num[i-1]);
29                 }
30             }
31         }
32     }
33     int maxx=0,minn=9999999;
34     for(int i=1;i<=n;i++)
35     {
36         maxx=max(maxx,dp1[i][i+n-1]);
37         minn=min(minn,dp2[i][i+n-1]);
38     }
39     cout<<minn<<endl<<maxx<<endl;
40     return 0;
41 } 

石子合并

 

于是区间dp思路就很明确了：

1.枚举区间长度

2.枚举左端点（通过左端点求长度）

3.枚举中间节点（中间决策状态）

阶段、状态、决策，三者应该按照从外到内的顺序依次循环。