数据结构（图的遍历和马踏棋盘算法）

Posted 2020-11-29 tianliang-2000

图的遍历

　　有两种方法：深度优先，广度优先

 

深度优先遍历

• 约定左手原则，在没有遇到重复顶点的情况下，分叉路口是从向右手边走，每走过一个顶点就做一个记号
• 如果分叉路所通向的结点已经全部走过，则返回上一个结点（回溯）
• 由此方法，直到返回这个顶点是结束

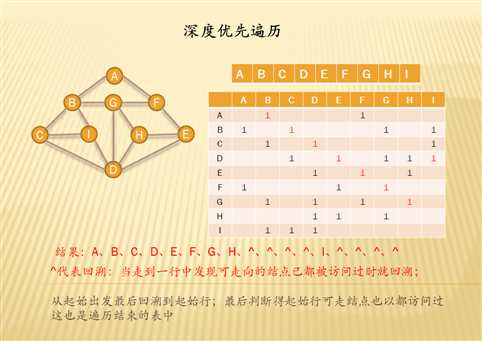
邻接矩阵中实现思路：

• 从A[0][0]开始，连向第一行中的第一个为1的元素A[ i ][ j ]；
• 然后跳到第 j 行继续找到第一个为1的元素，并确定这个元素是否走过，如果走过，则返回上一次跳转的行；第0行所对应结点全部走过

代码实现

 1 #include <stdio.h>
 2 #include <malloc.h>
 3 #define SIZE 9
 4 
 5 void user(char *lin,int n){
 6     printf("%c  ",lin[n]);
 7 }
 8 
 9 void depthTraversal(char *lin,int (*arr)[SIZE],int n){
10     int i=0,j=n;
11     static int tab[]={0,0,0,0,0,0,0,0,0};
12     tab[j]=1;
13     user(lin,j);
14     for(i=0;i<SIZE;i++){
15         if(i==j)
16             continue;
17         if(*(*(arr+j)+i)==1 && tab[i]==0)
18             depthTraversal(lin,arr,i);
19     }
20 }
21 
22 void main(){
23     char lin[]={‘A‘,‘B‘,‘C‘,‘D‘,‘E‘,‘F‘,‘G‘,‘H‘,‘I‘};
24     int arr[9][9]={
25            {0,1,0,0,0,1,0,0,0},
26            {1,0,1,0,0,0,1,0,1},
27            {0,1,0,1,0,0,0,0,1},
28            {0,0,1,0,1,0,1,1,1},
29            {0,0,0,1,0,1,0,1,0},
30            {1,0,0,0,1,0,1,0,0},
31            {0,1,0,1,0,1,0,1,0},
32            {0,0,0,1,1,0,1,0,0},
33            {0,1,1,1,0,0,0,0,0}
34         };
35     depthTraversal(lin,arr,0);
36     printf("
");
37 }

马踏棋盘算法

　　问题概述：在国际棋盘（8*8）中将‘马’放在任意指定的方框中，按照‘马’走‘日’的规则将马进行移动。要求每个方格只能进入一次，最终使马走遍棋盘64个方格。

　　解决方法：利用深度遍历的方法（回溯）；使马遇到死路时就回溯，直到走遍棋盘；

注：在(n*n)的棋盘上，当 n ≥ 5且为偶数时，以任一点都有解

  1 #include <stdio.h>
  2 #include <malloc.h>
  3 #define X 8
  4 #define Y 8
  5 
  6 int arr[X][Y];
  7 
  8 int nextxy(int *x,int*y,int count){
  9     switch(count){
 10         case 0:
 11             if(*x+2<=X-1 && *y-1>=0 && arr[*x+2][*y-1]==0){
 12                 *x+=2;
 13                 *y-=1;
 14                 return 1;
 15             }
 16             break;
 17         case 1:
 18             if(*x+2<=X-1 && *y+1<=Y-1 && arr[*x+2][*y+1]==0){
 19                 *x+=2;
 20                 *y+=1;
 21                 return 1;
 22             }
 23             break;
 24         case 2:
 25             if(*x+1<=X-1 && *y-2>=0 && arr[*x+1][*y-2]==0){
 26                 *x+=1;
 27                 *y-=2;
 28                 return 1;
 29             }
 30             break;
 31         case 3:
 32             if(*x+1<=X-1 && *y+2<=Y-1 && arr[*x+1][*y+2]==0){
 33                 *x+=1;
 34                 *y+=2;
 35                 return 1;
 36             }
 37             break;
 38         case 4:
 39             if(*x-2>=0 && *y-1>=0 && arr[*x-2][*y-1]==0){
 40                 *x-=2;
 41                 *y-=1;
 42                 return 1;
 43             }
 44             break;
 45         case 5:
 46             if(*x-2>=0 && *y+1<=Y-1 && arr[*x-2][*y+1]==0){
 47                 *x-=2;
 48                 *y+=1;
 49                 return 1;
 50             }
 51             break;
 52         case 6:
 53             if(*x-1>=0 && *y-2>=0 && arr[*x-1][*y-2]==0){
 54                 *x-=1;
 55                 *y-=2;
 56                 return 1;
 57             }
 58             break;
 59         case 7:
 60             if(*x-1>=0 && *y+2<=Y-1 && arr[*x-1][*y+2]==0){
 61                 *x-=1;
 62                 *y+=2;
 63                 return 1;
 64             }
 65             break;
 66         default:
 67             break;
 68     }
 69     return 0;
 70 }
 71 
 72 void Print(){
 73     int i,j;
 74     for(i=0;i<X;i++){
 75         for(j=0;j<Y;j++){
 76             printf("%d	",arr[i][j]);
 77         }
 78         printf("
");
 79     }
 80     printf("
");
 81 }
 82 
 83 //(x,y)为位置坐标
 84 //tag是标记变量，也用于记录步骤
 85 int TravelBoard(int x,int y,int tag){
 86     int x1=x,y1=y;
 87     int i=0;
 88     int flag=0;//记录当前位置的选者是否会导致失败
 89     arr[x][y]=tag;
 90     if(X*Y==tag){
 91         Print();//打印
 92         return 1;
 93     }
 94     //找到马下一个可走的坐标（x1,y1）,如果找到flag=1,否者为0
 95     flag=nextxy(&x1,&y1,i);
 96     while(0==flag &&i<8){
 97         i++;
 98         flag=nextxy(&x1,&y1,i);
 99     }
100 
101     while(flag){//这里的flag记录是否结束（失败）
102         if(TravelBoard(x1,y1,tag+1)){
103             return 1;
104         }
105 
106         //这个位置会导致后面碰壁失败，需要回溯到上个位置
107         x1=x;
108         y1=y;
109         i++;
110         flag=nextxy(&x1,&y1,i);
111         while(0==flag &&i<8){
112             i++;
113             flag=nextxy(&x1,&y1,i);
114         }
115     }
116     if(flag==0){
117         arr[x][y]=0;
118     }
119     return 0;
120 }
121 
122 void main(){
123     int i,j;
124     for(i=0;i<X;i++){
125         for(j=0;j<Y;j++){
126             arr[i][j]=0;
127         }
128     }
129     printf("请输入起始位置的行：");
130     scanf("%d",&i);
131     printf("请输入起始位置的列：");
132     scanf("%d",&j);
133     //建议用两行一列测试
134 
135     if(!TravelBoard(i,j,1)){
136         printf("马踏棋盘失败");
137     }
138 }

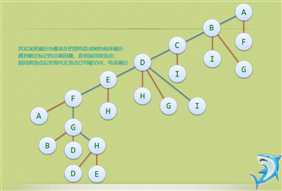
广度优先遍历

　　其实广度优先遍历，类似与树的层序遍历

　　方法：

• 任意选一顶点，放入队列中；
• 在队列中让第一个位置进行操作，遍历这个顶点的所有连接的顶点，依次加入到这个队列中（加入时做好标记以免重复添加）；删除刚刚操作的队头顶点
• 重复 ② 步骤，直到队列中全部结点出队列