华为云技术分享Rust 算法排位记 - 插入排序的图示和代码实现

Posted 2020-11-28 huaweicloud

Rust 代码在编写过程中与其它语言的略有不同，因为它的编译器不允许有任何不安全的写法，遂代码编写过程中花费时间最长的莫过于查找编译报错的原因。这样也有好处——代码写好之后，稳定性高得一笔！

以下是来自菜鸟教程中的排序定义和动图示意：

插入排序（英语：Insertion Sort）是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

我们来捋一捋，插入排序的主要逻辑为：

1. 外循环先指定一个数，通常是第一个数
2. 接着在内循环中将这个外循环指定数与左侧数逐个比较，并根据比较结果将外循环指定数插入在内循环数的左边或不动
3. 左侧为排序好的元素，遂内循环中的比较是外循环指定数不停地与左侧元素进行比较
4. 当外循环指定数小于左侧元素时交换位置，否则不动
5. 以此类推，直到外层循环结束

现在有一组需要排序的元素：

[7, 21, 9, 13, 109, 9, 2, 50, 33, -1, 20, 11]

按照插入排序的逻辑外循环指定第一个数 7，选定后 for 循环将从下标为 1 的元素开始循环。代码表现为：

for i in 1..vectors.len(){}

下标为 0 的第一个数 7 是排序好的，那么 for 循环从下标为 1 的第二个数 21 开始。在内循环中将这个外循环指定数与左侧数 [7] 逐个比较，当外循环指定数小于左边元素时交换位置，否则不动。

此时进入下一轮外循环，指定下标为 2 的第三个数 9。在内循环中将这个外循环指定数与左侧数 [7, 21] 逐个比较，当外循环指定数小于左边元素 21 时交换位置，遇到 7 不动。遂元素组变为 ：

[7, 9, 21, 13, 109, 9, 2, 50, 33, -1, 20, 11]

此时进入下一轮外循环，指定下标为 3 的第四个数 13。在内循环中将这个外循环指定数与左侧数 [7, 9, 21] 逐个比较，当外循环指定数小于左边元素 21 时交换位置，遇到 9 不动。遂元素组变为 ：

[7, 9, 13, 21, 109, 9, 2, 50, 33, -1, 20, 11]

依此类推 ...

此时进入第 N 轮外循环，指定下标为 5 的第六个数 9。在内循环中将这个外循环指定数与左侧数 [7, 9, 13, 21, 109] 逐个比较：

• 当外循环指定数小于左边元素 109 时交换位置；
• 当外循环指定数小于左边元素 21 时交换位置；
• 当外循环指定数小于左边元素 13 时交换位置；

遇到 9 不动。遂元素组变为 ：

[7, 9, 9, 13, 21, 109, 2, 50, 33, -1, 20, 11]

此时进入第 N 轮外循环，指定下标为 6 的第七个数 2。在内循环中将这个外循环指定数与左侧数 [7, 9, 9, 13, 21, 109] 逐个比较：

• 当外循环指定数小于左边元素 109 时交换位置；
• 当外循环指定数小于左边元素 21 时交换位置；
• 当外循环指定数小于左边元素 13 时交换位置；
• 当外循环指定数小于左边元素 9 时交换位置；
• 当外循环指定数小于左边元素 9 时交换位置；
• 当外循环指定数小于左边元素 7 时交换位置；

遍历至元素组左侧尽头，此时 j 不大于等于 0，内循环结束。遂元素组变为 ：

[2, 7, 9, 9, 13, 21, 109, 50, 33, -1, 20, 11]

在此之前，2 的左侧有很多元素，它需要与这些元素逐个比较并交换位置。数字 2 的位置变化过程如下：

1 [7, 9, 9, 13, 21, 2, 109, 50, 33, -1, 20, 11]
2 [7, 9, 9, 13, 2, 21, 109, 50, 33, -1, 20, 11]
3 [7, 9, 9, 2, 13, 21, 109, 50, 33, -1, 20, 11]
4 [7, 9, 2, 9, 13, 21, 109, 50, 33, -1, 20, 11]
5 [7, 2, 9, 9, 13, 21, 109, 50, 33, -1, 20, 11]
6 [2, 7, 9, 9, 13, 21, 109, 50, 33, -1, 20, 11]

从过程中可看到，内循环的每一轮，数字 2 都会往左移动，直到前面没有比 2 大的数字。

以此规则类推，元素排序的最终结果为：

[-1, 2, 7, 9, 9, 11, 13, 20, 21, 33, 50, 109]

具体代码实现

首先定义一组元素，并打印：

1 fn main() {
2     let mut vectors = vec![7, 21, 9, 13, 109, 9, 2, 50, 33, -1, 20, 11];
3     println!("vectors: {:?}", vectors);
4 }

然后定义排序方法：

1 fn insert_sort(vectors: &mut Vec<i32>) -> &Vec<i32>{
2         vectors
3 }

排序方法的外循环是 for 循环：

1 fn insert_sort(vectors: &mut Vec<i32>) -> &Vec<i32>{
2         for i in 1..vectors.len(){
3         
4     }
5         vectors
6 }

这里将外层元素赋值给可变变量 current，同时设定内循环左侧元素的下标：

1 fn insert_sort(vectors: &mut Vec<i32>) -> &Vec<i32>{
2         for i in 1..vectors.len(){
3             let mut current = vectors[i];
4             let mut j = i - 1;
5     }
6         vectors
7 }

在内循环中的将这个外循环指定数与左侧数逐个比较，当外循环指定数小于左侧元素时交换位置，否则不动。

与左侧元素比较用 j = i - 1, vectors[j] 表示；

不停地与左侧元素比较用 while j >= 0, j = j -1 表示；

比较用 current < vectors[j] 表示；

交换位置无法像 Python 那样 a, b = b, a，只能用 c = a, a = b, b = c 这种加入第三个数的方式倒腾。遂代码如下

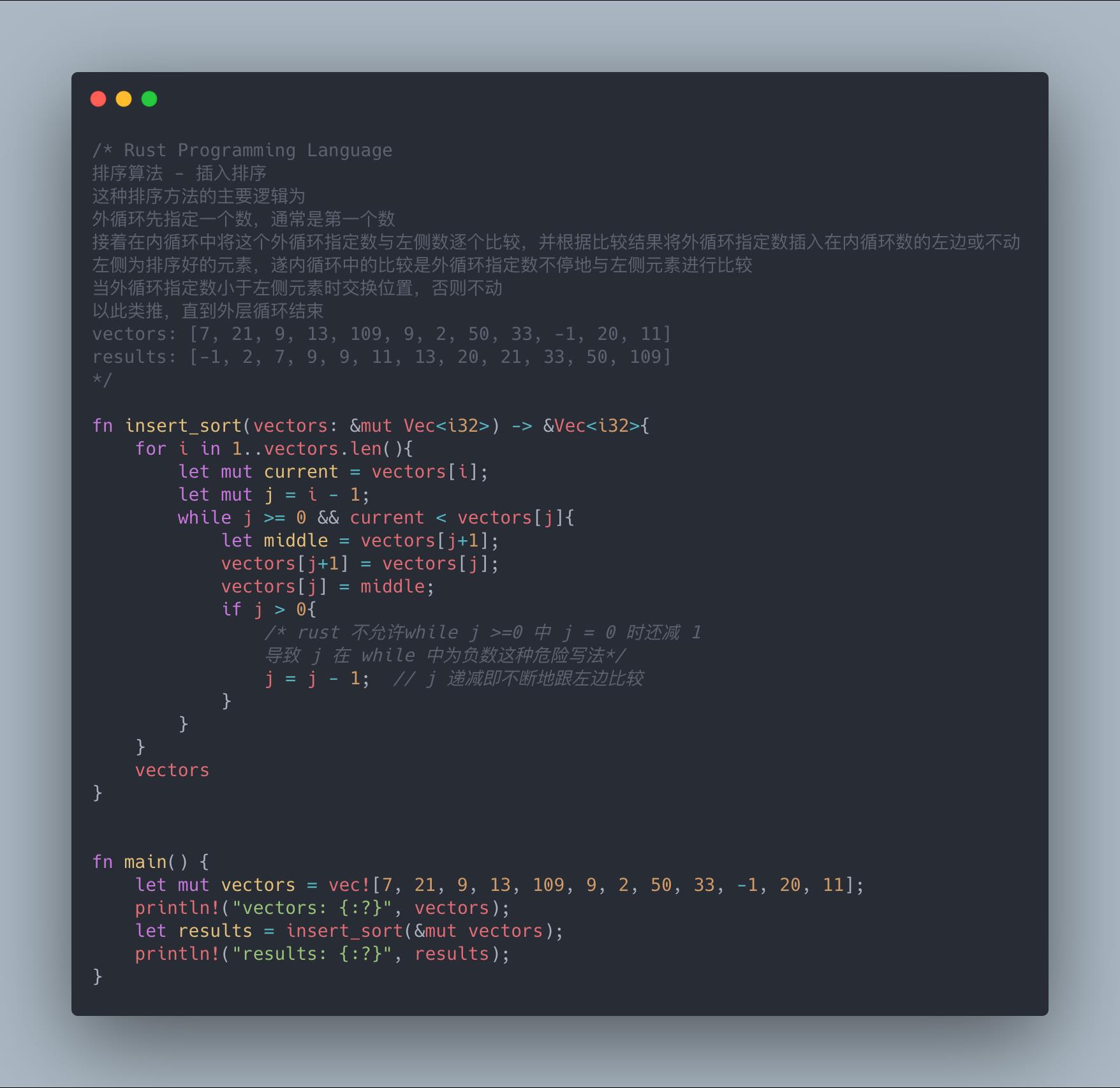
 1 fn insert_sort(vectors: &mut Vec<i32>) -> &Vec<i32>{
 2     for i in 1..vectors.len(){
 3         let mut current = vectors[i];
 4         let mut j = i - 1;
 5         while j >= 0 && current < vectors[j]{
 6             let middle = vectors[j+1];
 7             vectors[j+1] = vectors[j];
 8             vectors[j] = middle;
 9             j = j - 1;
10         }
11     }
12     vectors
13 }

不过这样写的话，外循环指定数为比左侧所有数都小的情况下会无法通过编译的。例如外循环指定数为 2 时需要与左侧所有数进行比较，直到 j = 0，但 while 中最后一句是 j = j - 1，运行到这里后 j = -1。按照正常运行流程，程序会进入到下一轮 while j >= 0 的内循环，但由于 j = -1，就不会进入 while 循环体。Python 语言这样写是没问题的，但 Rust 的编译器不允许，遂需要在 j = j - 1 外层增加控制语句 if j = 0。

理论的验证

上面的理论看似有理有据令人信服，但究竟对不对呢？

有没有可能分析错误呢？

虽然程序是对的，但万一描述出来的逻辑有误呢？

我们可以通过打印程序执行过程中的外循环指定数 current、内循环左侧第一个数和每次交换位置后元素组 vectors 来观察循环比较时元素位置的变化情况。添加了打印语句的代码如下：

 1 fn insert_sort(vectors: &mut Vec<i32>) -> &Vec<i32>{
 2     for i in 1..vectors.len(){
 3         let mut current = vectors[i];
 4         let mut j = i - 1;
 5         println!("current vectors: {:?}", vectors);
 6         println!("current: {} < vectors[j]: {}", current, vectors[j]);
 7         while j >= 0 && current < vectors[j]{
 8             let middle = vectors[j+1];
 9             vectors[j+1] = vectors[j];
10             vectors[j] = middle;
11             if j > 0{
12                 /* rust 不允许while j >=0 中 j = 0 时还减 1
13                 导致 j 在 while 中为负数这种危险写法*/
14                 j = j - 1;  // j 递减即不断地跟左边比较
15             }
16             println!("after vectors: {:?}", vectors);
17         }
18     }
19     vectors
20 }

代码运行后的打印结果如为：

 1 vectors: [7, 21, 9, 13, 109, 9, 2, 50, 33, -1, 20, 11]
 2 current vectors: [7, 21, 9, 13, 109, 9, 2, 50, 33, -1, 20, 11]
 3 current: 21 < vectors[j]: 7
 4 current vectors: [7, 21, 9, 13, 109, 9, 2, 50, 33, -1, 20, 11]
 5 current: 9 < vectors[j]: 21
 6 after vectors: [7, 9, 21, 13, 109, 9, 2, 50, 33, -1, 20, 11]
 7 current vectors: [7, 9, 21, 13, 109, 9, 2, 50, 33, -1, 20, 11]
 8 current: 13 < vectors[j]: 21
 9 after vectors: [7, 9, 13, 21, 109, 9, 2, 50, 33, -1, 20, 11]
10 current vectors: [7, 9, 13, 21, 109, 9, 2, 50, 33, -1, 20, 11]
11 current: 109 < vectors[j]: 21
12 current vectors: [7, 9, 13, 21, 109, 9, 2, 50, 33, -1, 20, 11]
13 current: 9 < vectors[j]: 109
14 after vectors: [7, 9, 13, 21, 9, 109, 2, 50, 33, -1, 20, 11]
15 after vectors: [7, 9, 13, 9, 21, 109, 2, 50, 33, -1, 20, 11]
16 after vectors: [7, 9, 9, 13, 21, 109, 2, 50, 33, -1, 20, 11]
17 current vectors: [7, 9, 9, 13, 21, 109, 2, 50, 33, -1, 20, 11]
18 current: 2 < vectors[j]: 109
19 after vectors: [7, 9, 9, 13, 21, 2, 109, 50, 33, -1, 20, 11]
20 after vectors: [7, 9, 9, 13, 2, 21, 109, 50, 33, -1, 20, 11]
21 after vectors: [7, 9, 9, 2, 13, 21, 109, 50, 33, -1, 20, 11]
22 after vectors: [7, 9, 2, 9, 13, 21, 109, 50, 33, -1, 20, 11]
23 after vectors: [7, 2, 9, 9, 13, 21, 109, 50, 33, -1, 20, 11]
24 after vectors: [2, 7, 9, 9, 13, 21, 109, 50, 33, -1, 20, 11]
25 current vectors: [2, 7, 9, 9, 13, 21, 109, 50, 33, -1, 20, 11]
26 current: 50 < vectors[j]: 109
27 after vectors: [2, 7, 9, 9, 13, 21, 50, 109, 33, -1, 20, 11]
28 current vectors: [2, 7, 9, 9, 13, 21, 50, 109, 33, -1, 20, 11]
29 current: 33 < vectors[j]: 109
30 after vectors: [2, 7, 9, 9, 13, 21, 50, 33, 109, -1, 20, 11]
31 after vectors: [2, 7, 9, 9, 13, 21, 33, 50, 109, -1, 20, 11]
32 current vectors: [2, 7, 9, 9, 13, 21, 33, 50, 109, -1, 20, 11]
33 current: -1 < vectors[j]: 109
34 after vectors: [2, 7, 9, 9, 13, 21, 33, 50, -1, 109, 20, 11]
35 after vectors: [2, 7, 9, 9, 13, 21, 33, -1, 50, 109, 20, 11]
36 after vectors: [2, 7, 9, 9, 13, 21, -1, 33, 50, 109, 20, 11]
37 after vectors: [2, 7, 9, 9, 13, -1, 21, 33, 50, 109, 20, 11]
38 after vectors: [2, 7, 9, 9, -1, 13, 21, 33, 50, 109, 20, 11]
39 after vectors: [2, 7, 9, -1, 9, 13, 21, 33, 50, 109, 20, 11]
40 after vectors: [2, 7, -1, 9, 9, 13, 21, 33, 50, 109, 20, 11]
41 after vectors: [2, -1, 7, 9, 9, 13, 21, 33, 50, 109, 20, 11]
42 after vectors: [-1, 2, 7, 9, 9, 13, 21, 33, 50, 109, 20, 11]
43 current vectors: [-1, 2, 7, 9, 9, 13, 21, 33, 50, 109, 20, 11]
44 current: 20 < vectors[j]: 109
45 after vectors: [-1, 2, 7, 9, 9, 13, 21, 33, 50, 20, 109, 11]
46 after vectors: [-1, 2, 7, 9, 9, 13, 21, 33, 20, 50, 109, 11]
47 after vectors: [-1, 2, 7, 9, 9, 13, 21, 20, 33, 50, 109, 11]
48 after vectors: [-1, 2, 7, 9, 9, 13, 20, 21, 33, 50, 109, 11]
49 current vectors: [-1, 2, 7, 9, 9, 13, 20, 21, 33, 50, 109, 11]
50 current: 11 < vectors[j]: 109
51 after vectors: [-1, 2, 7, 9, 9, 13, 20, 21, 33, 50, 11, 109]
52 after vectors: [-1, 2, 7, 9, 9, 13, 20, 21, 33, 11, 50, 109]
53 after vectors: [-1, 2, 7, 9, 9, 13, 20, 21, 11, 33, 50, 109]
54 after vectors: [-1, 2, 7, 9, 9, 13, 20, 11, 21, 33, 50, 109]
55 after vectors: [-1, 2, 7, 9, 9, 13, 11, 20, 21, 33, 50, 109]
56 after vectors: [-1, 2, 7, 9, 9, 11, 13, 20, 21, 33, 50, 109]
57 results: [-1, 2, 7, 9, 9, 11, 13, 20, 21, 33, 50, 109]

由此可见，理论部分的描述是正确的

完整的 Rust 插入排序代码如下：

Rust 算法代码仓库地址 github.com/asyncins/ac…

作者：华为云云享专家 韦世东