算法基础

Posted 2020-11-28 kai-

目录

• 算法
• 时间复杂度
• 空间复杂度
• 冒泡排序
• 选择排序
• 插入排序
• 快速排序

算法

时间复杂度

算法的时间复杂度是一个函数，它定量描述了该算法的运行时间，时间复杂度常用“O”表述，使用这种方式时，时间复杂度可被称为是渐近的，它考察当输入值大小趋近无穷时的情况

时间复杂度小结：

时间复杂度是用来估计算法运行时间的一个式子（单位）

一般来说，时间复杂度高的算法比复杂度低的算法慢

常见的时间复杂度（按效率排序）

O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n3)

不常见的时间复杂度（看看就好）

O(n!) O(2n) O(nn) …

如何一眼判断时间复杂度

循环减半的过程 O(logn)
几次循环就是 n 的几次方的复杂度

空间复杂度

空间复杂度：用来评估算法内存占用大小的一个式子

“空间换时间”

冒泡排序

思路：首先，列表每两个相邻的数，如果前边的比后边的大，那么交换这两个数

def bubble_sort(li):
    for i in range(len(li)-1):
        for j in range(len(li)-i-1):
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]

时间复杂度：O(n2)

冒泡排序优化

如果冒泡排序中执行一趟而没有交换，则列表已经是有序状态，可以直接结束算法

def bubble_sort(li):
    for i in range(len(li)-1):
        flag = True
        for j in range(len(li)-1-i):
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]
                flag = False
        if flag:
            return

选择排序

思路：一趟遍历记录最小的数，放到第一个位置；
再一趟遍历记录剩余列表中最小的数，继续放置；

def select_sort(li):
    for i in range(len(li)):
        minLoc = i
        for j in range(i+1, len(li)):
            if li[minLoc] > li[j]:
                li[minLoc], li[j] = li[j], li[minLoc]

时间复杂度：O(n2)

插入排序

列表被分为有序区和无序区两个部分。最初有序区只有一个元素。
每次从无序区选择一个元素，插入到有序区的位置，直到无序区变空

li = [5, 7, 4, 6, 3, 1, 2, 9, 8]
def insert_sort(li):
    for i in range(1, len(li)):  ### i=2
        tmp = li[i] ## tmp=li[2]=4
        j = i - 1  ### j = 1 li[1]=7

        while j >= 0 and li[j] > tmp:
            li[j+1] = li[j]  ### [5,7,7,6,3,8,2,9,1]  ==> [5,5,7,6,3,8,2,9,1]
            j = j - 1   ### j = 0  j= -1

        li[j+1] = tmp

时间复杂度：O(n2)

快速排序

快排思路：
取一个元素p（第一个元素），使元素p归位；
列表被 p 分成两部分，左边都比 p 小，右边都比 p 大；
递归完成排序。

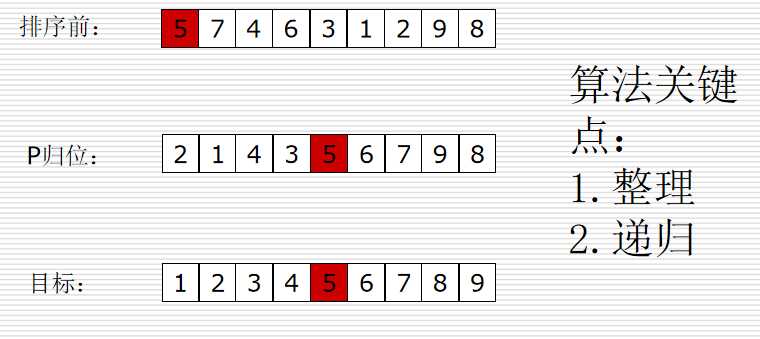
##### 时间复杂度是：O(nlogn)
def partition(li, left, right):  #### O(n)

    tmp = li[left]  # 把最左边的存到一个变量里

    while left < right:
        while left < right and li[right] >= tmp:  # 如果最右边的比最左边的大
            right = right - 1  # right 指针向左移 1，再继续下次比较，结果还是大，继续往左移1，如果比left小，跳出循环，移到最左边
        li[left] = li[right]

        while left < right and li[left] <= tmp:
            left = left + 1
        li[right] = li[left]

    li[left] = tmp  # 此时left和right重合到了一起，就可以让最开始的那个变量归位了

    return left

def quick_sort(li, left, right):

    if left < right:
        mid = partition(li, left, right)  ### 归位函数

        # 递归
        quick_sort(li, left, mid-1)     #### O(logn)
        quick_sort(li, mid+1, right)

时间复杂度是：O(nlogn)