盛最多水的容器
Posted pigdragon
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了盛最多水的容器相关的知识,希望对你有一定的参考价值。
给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。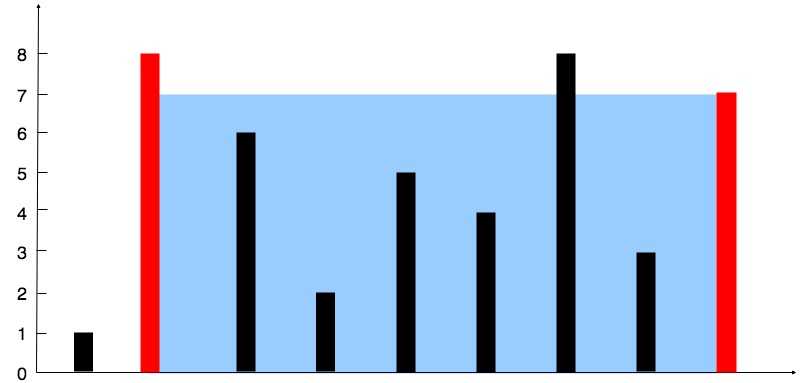
示例:
输入: [1,8,6,2,5,4,8,3,7]
输出: 49
方法一:
首先想到的肯定是暴力破解法,两层循环,算出所有可能的情况,找到最大值,时间复杂度是O(N^2),思路没什么值得解释的,代码如下:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MIN(x,y) (x<y?x:y)
int maxArea(int *height, int heightSize){
int max_area=0;
int i, j;
for(i=0;i<heightSize;i++){
for(j=i+1;j<heightSize;j++){
int high=MIN(height[i], height[j]);
int area=high*(j-i);
if(area>max_area)
max_area=area;
}
}
return max_area;
}
方法二:
该方法使用了双指针,用一句话概括双指针解法的要点:指针每一次移动,都意味着排除掉了一个柱子。
如下图所示,在一开始,我们考虑相距最远的两个柱子所能容纳水的面积。水的宽度是两根柱子之间的距离 d=8d = 8d=8;
如下图所示,在一开始,我们考虑相距最远的两个柱子所能容纳水的面积。水的宽度是两根柱子之间的距离 d=8d = 8d=8;
水的高度取决于两根柱子之间较短的那个,即左边柱子的高度 h=3h = 3h=3。水的面积就是 3×8=24。
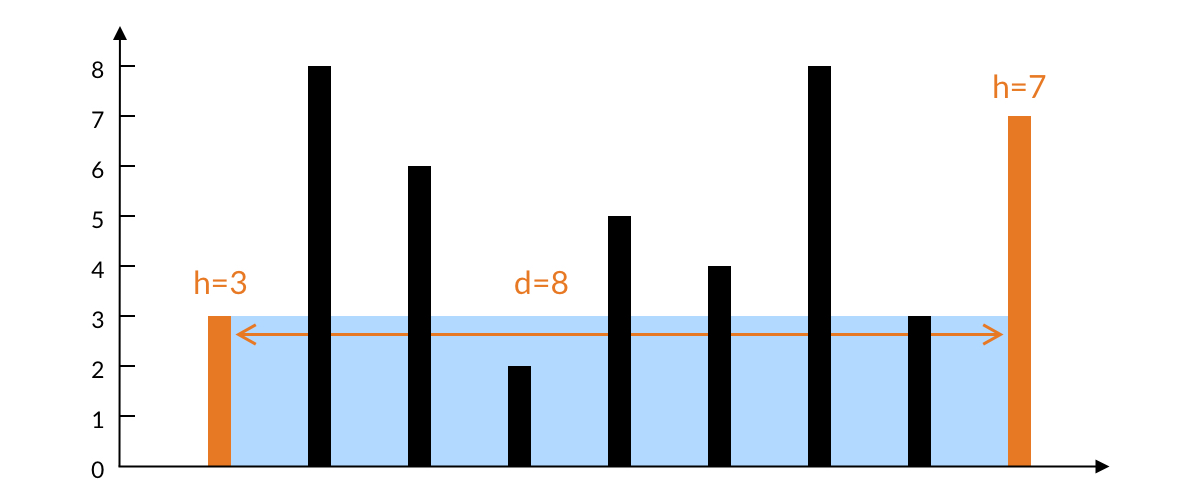
如果选择固定一根柱子,另外一根变化,水的面积会有什么变化吗?稍加思考可得:
当前柱子是最两侧的柱子,水的宽度 d 为最大,其他的组合,水的宽度都比这个小。
左边柱子较短,决定了水的高度为 3。如果移动左边的柱子,新的水面高度不确定,一定不会超过右边的柱子高度 7。
如果移动右边的柱子,新的水面高度一定不会超过左边的柱子高度 3,也就是不会超过现在的水面高度。
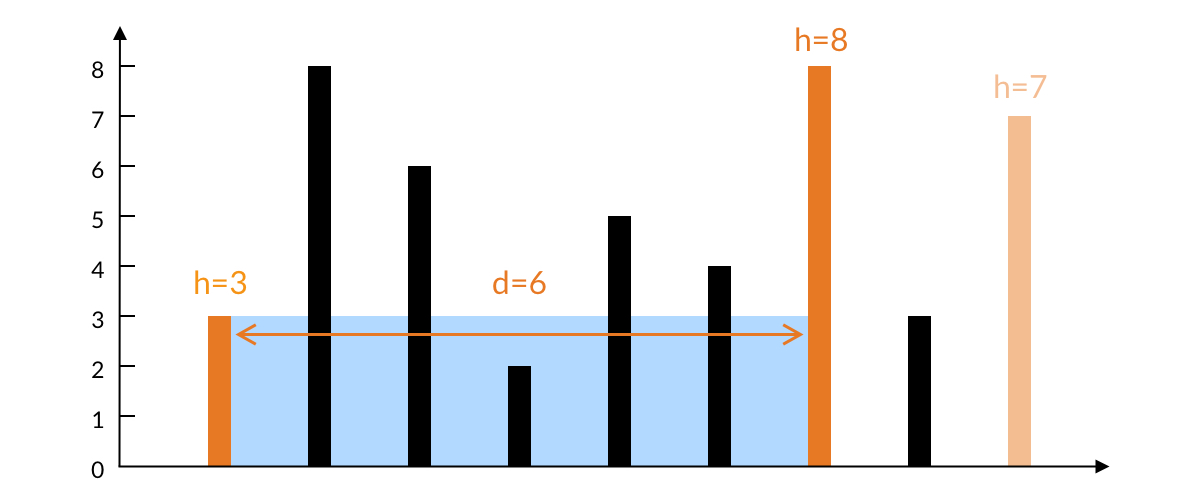
由此可见,如果固定左边的柱子,移动右边的柱子,那么水的高度一定不会增加,且宽度一定减少,所以水的面积一定减少。这个时候,左边的柱子和任意一个其他柱子的组合,其实都可以排除了。也就是我们可以排除掉左边的柱子了。
这个排除掉左边柱子的操作,就是双指针代码里的 i++。i 和 j 两个指针中间的区域都是还未排除掉的区域。随着不断的排除,i 和 j 都会往中间移动。当 i 和 j 相遇,算法就结束了。
图解双指针解法的原理
下面我们用更直观的方法来看看“排除掉一根柱子”、“指针移动”究竟代表着什么。
在这道题中,假设一共有 n根柱子,编号 0,1,…,n−1,高度分别为 H0?,H1?,…,Hn−1。我们要寻找的是两根柱子 i,j,它们需要满足的约束条件是:
i、j 都是合法的柱子下标,即 0≤i<n,0≤j<n
i 在 j的左边,即 i<j
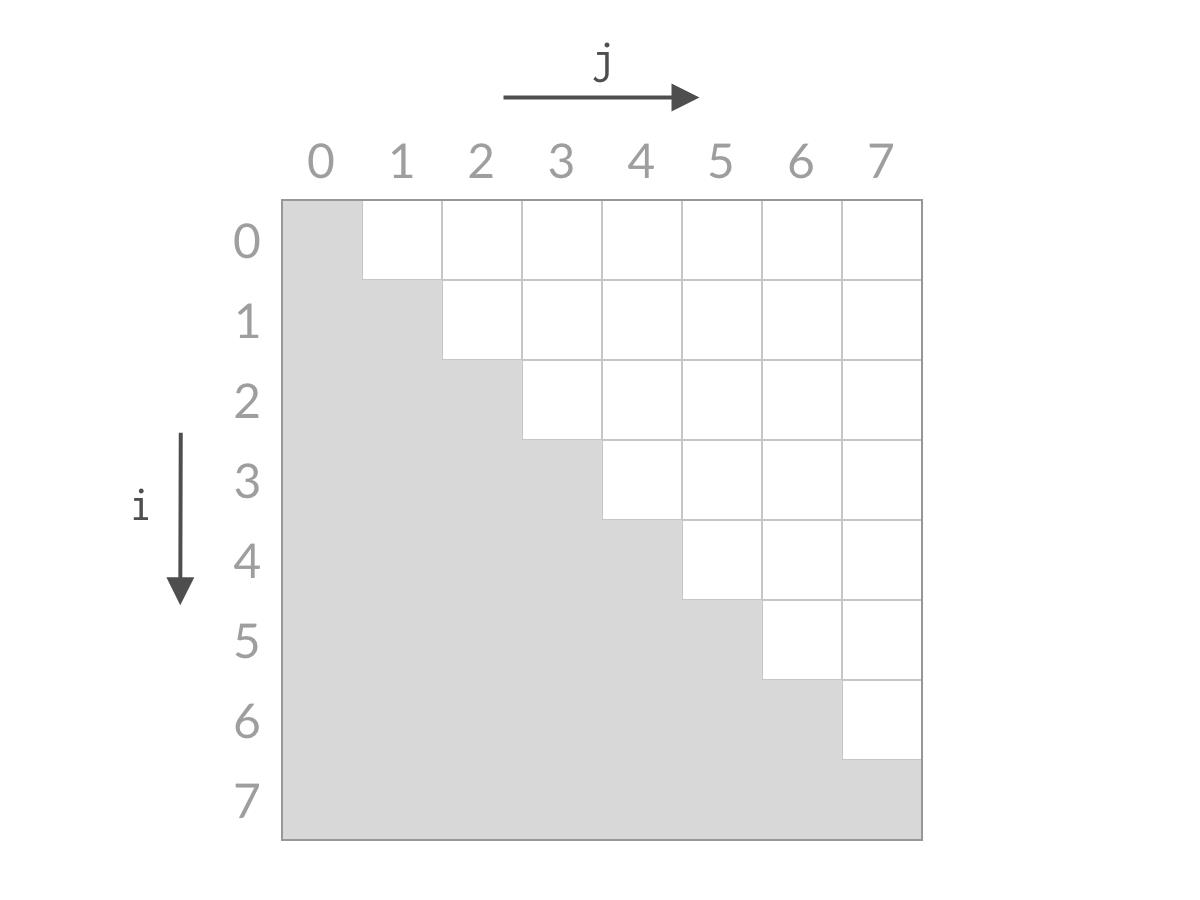
而我们希望从中找到容纳水面积最大的柱子 (i,j)。以 n=8 为例,这时候全部的搜索空间是:
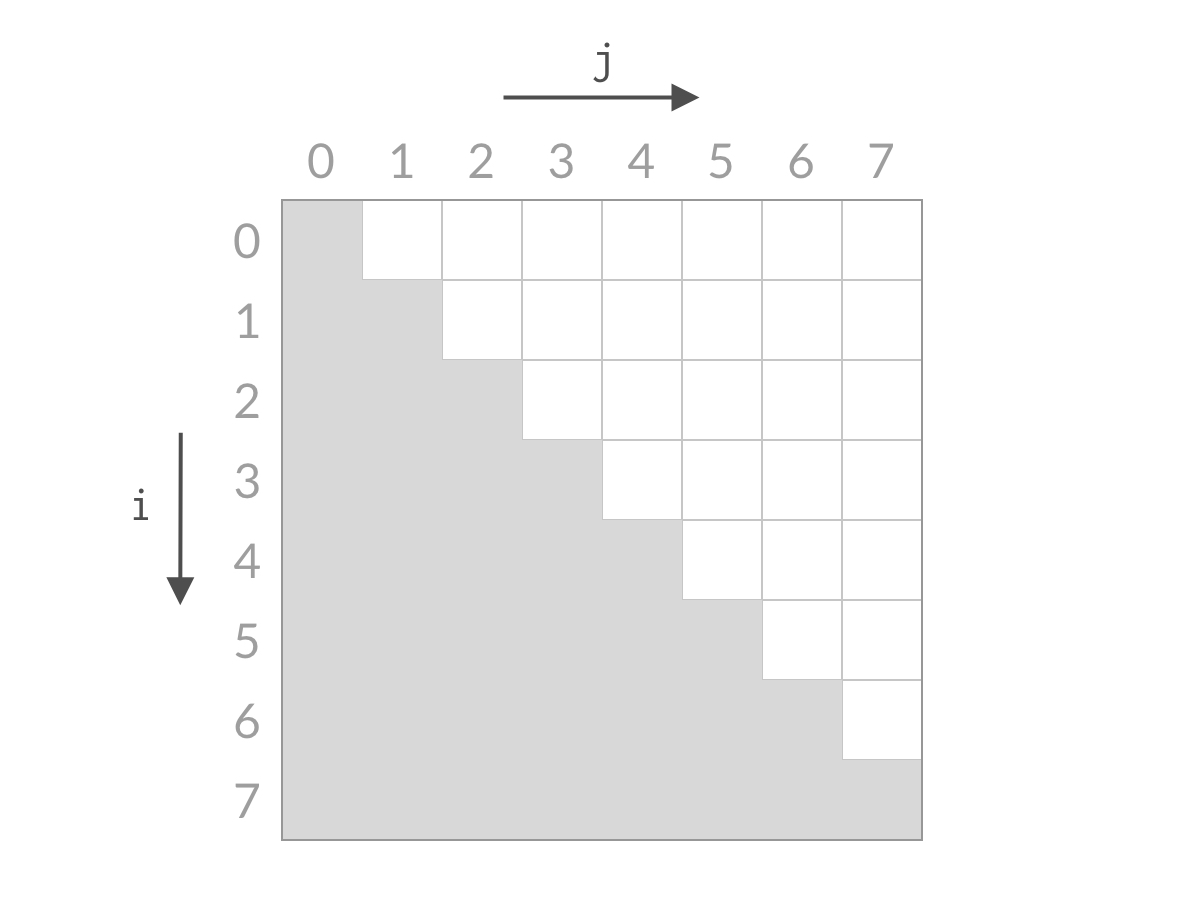
由于 i、j 的约束条件的限制,搜索空间是白色的倒三角部分。可以看到,搜索空间的大小是 O(n^2)数量级的。如果用暴力解法求解,一次只检查一个单元格,那么时间复杂度一定是 O(n^2)。要想得到 O(n)的解法,我们就需要能够一次排除多个单元格。那么我们来看看,本题的双指针解法是如何削减搜索空间的:
一开始,我们检查右上方单元格 (0,7),即考虑最左边的 0 号柱子和最右边的 7号柱子,计算它们之间容纳水的面积。然后我们比较一下两根柱子的高度,关注其中较短的一根。
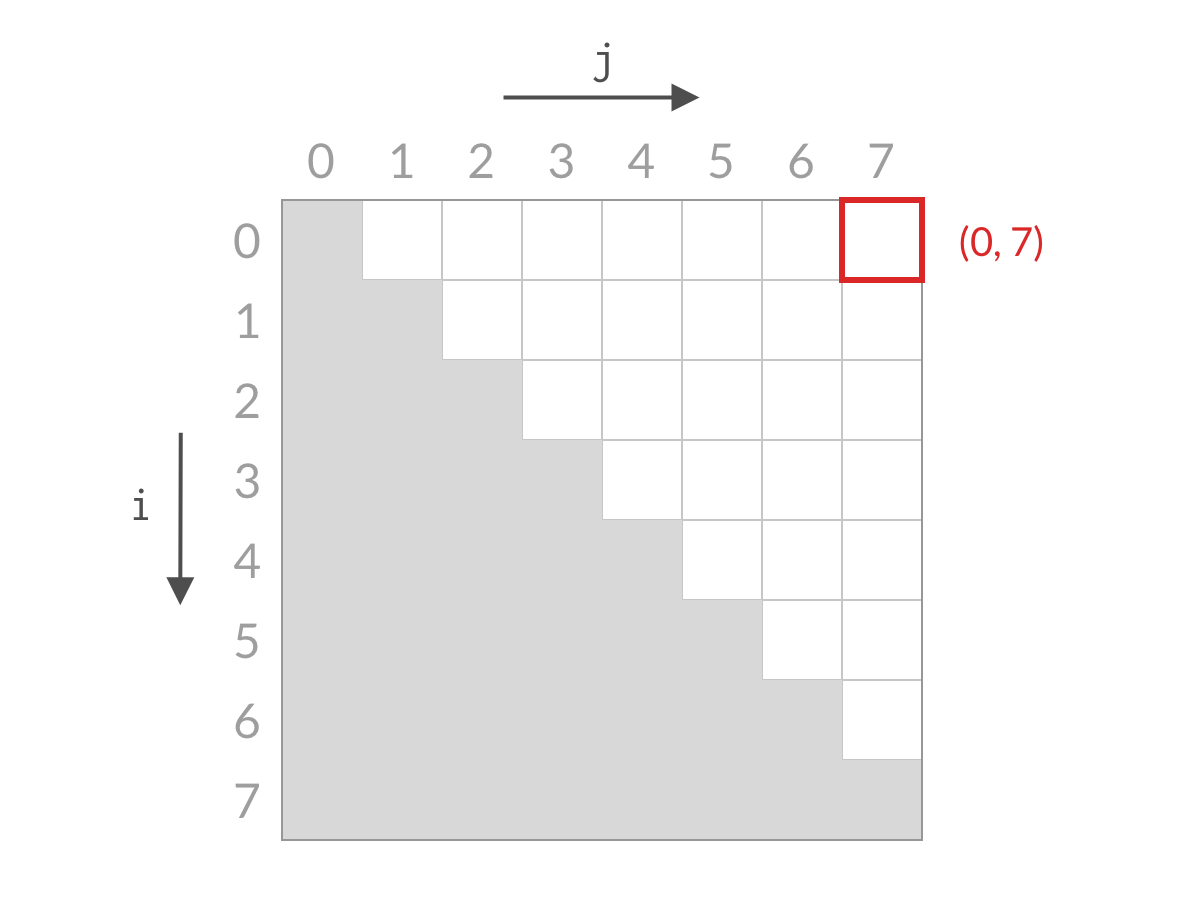
假设左边的 0 号柱子较短。根据刚才的推理,0号柱子目前的水面高度已经到了上限。由于 7号柱子已经是离 0 号柱子最远的了,水的宽度也最大。

如果选择固定一根柱子,另外一根变化,水的面积会有什么变化吗?稍加思考可得:
当前柱子是最两侧的柱子,水的宽度 d 为最大,其他的组合,水的宽度都比这个小。
左边柱子较短,决定了水的高度为 3。如果移动左边的柱子,新的水面高度不确定,一定不会超过右边的柱子高度 7。
如果移动右边的柱子,新的水面高度一定不会超过左边的柱子高度 3,也就是不会超过现在的水面高度。

由此可见,如果固定左边的柱子,移动右边的柱子,那么水的高度一定不会增加,且宽度一定减少,所以水的面积一定减少。这个时候,左边的柱子和任意一个其他柱子的组合,其实都可以排除了。也就是我们可以排除掉左边的柱子了。
这个排除掉左边柱子的操作,就是双指针代码里的 i++。i 和 j 两个指针中间的区域都是还未排除掉的区域。随着不断的排除,i 和 j 都会往中间移动。当 i 和 j 相遇,算法就结束了。
图解双指针解法的原理
下面我们用更直观的方法来看看“排除掉一根柱子”、“指针移动”究竟代表着什么。
在这道题中,假设一共有 n根柱子,编号 0,1,…,n−1,高度分别为 H0?,H1?,…,Hn−1。我们要寻找的是两根柱子 i,j,它们需要满足的约束条件是:
i、j 都是合法的柱子下标,即 0≤i<n,0≤j<n
i 在 j的左边,即 i<j
而我们希望从中找到容纳水面积最大的柱子 (i,j)。以 n=8 为例,这时候全部的搜索空间是:

由于 i、j 的约束条件的限制,搜索空间是白色的倒三角部分。可以看到,搜索空间的大小是 O(n^2)数量级的。如果用暴力解法求解,一次只检查一个单元格,那么时间复杂度一定是 O(n^2)。要想得到 O(n)的解法,我们就需要能够一次排除多个单元格。那么我们来看看,本题的双指针解法是如何削减搜索空间的:
一开始,我们检查右上方单元格 (0,7),即考虑最左边的 0 号柱子和最右边的 7号柱子,计算它们之间容纳水的面积。然后我们比较一下两根柱子的高度,关注其中较短的一根。

假设左边的 0 号柱子较短。根据刚才的推理,0号柱子目前的水面高度已经到了上限。由于 7号柱子已经是离 0 号柱子最远的了,水的宽度也最大。
如果换其他的柱子和 0 号柱子配对,水的宽度只会更小,高度也不会增加,容纳水的面积只会更小。
也就是说,0 号柱子和 6,5,…,1 号柱子的配对都可以排除掉了。记录了 (0,7)这组柱子的结果之后,就可以排除 0 号柱子了。这相当于 i=0的情况全部被排除。
对应于双指针解法的代码,就是 i++;对应于搜索空间,就是削减了一行的搜索空间,如下图所示。
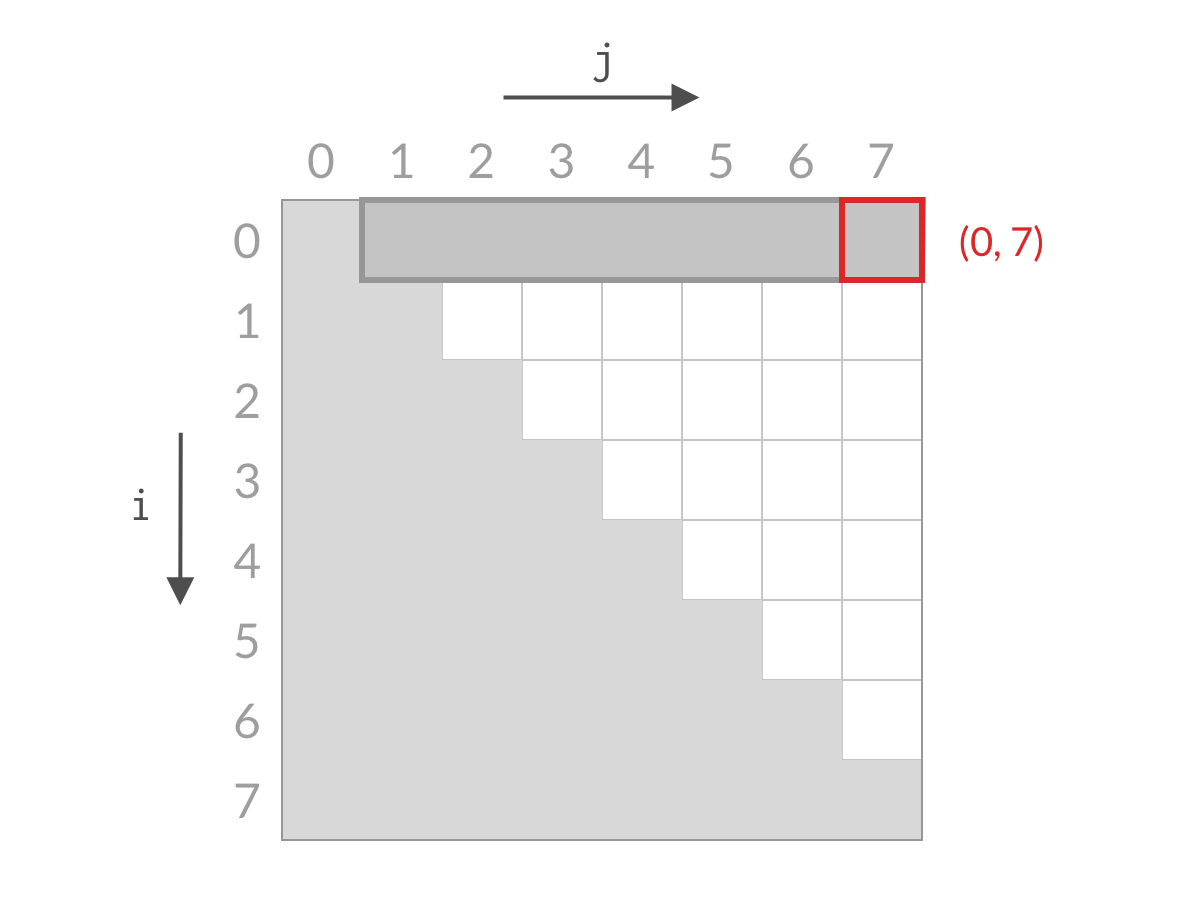
排除掉了搜索空间中的一行之后,我们再看剩余的搜索空间,仍然是倒三角形状。

排除掉了搜索空间中的一行之后,我们再看剩余的搜索空间,仍然是倒三角形状。
我们检查右上方的单元格 (1,7),即考虑 1号柱子和 7 号柱子,计算它们之间容纳水的面积。
然后,比较两根柱子的高度。
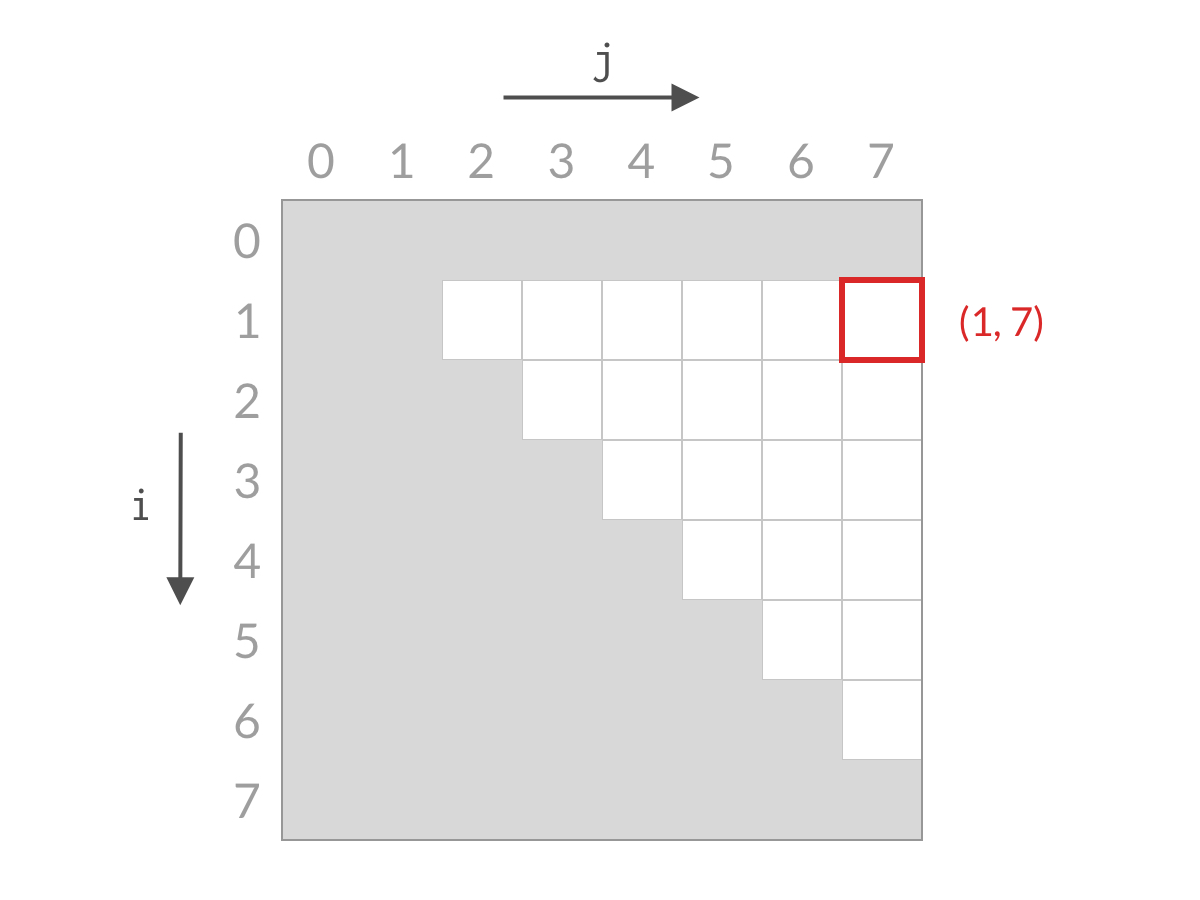
假设此时 7 号柱子较短。同理, 7 号柱子已经是离 1 号柱子最远的了,如果换其他的柱子和 7 号柱子配对,水的宽度变小,高度也不会增加,容纳水的面积只会更小。

假设此时 7 号柱子较短。同理, 7 号柱子已经是离 1 号柱子最远的了,如果换其他的柱子和 7 号柱子配对,水的宽度变小,高度也不会增加,容纳水的面积只会更小。
也就是说,7 号柱子和 2,3,…,6 号柱子的配对都可以排除掉了。
记录了 (1,7) 这组柱子的结果之后,就可以排除 7 号柱子了。这相当于 j=7的情况全部被排除。
对应于双指针解法的代码,就是 j--;对应于搜索空间,就是削减了一列的搜索空间,如下图所示。
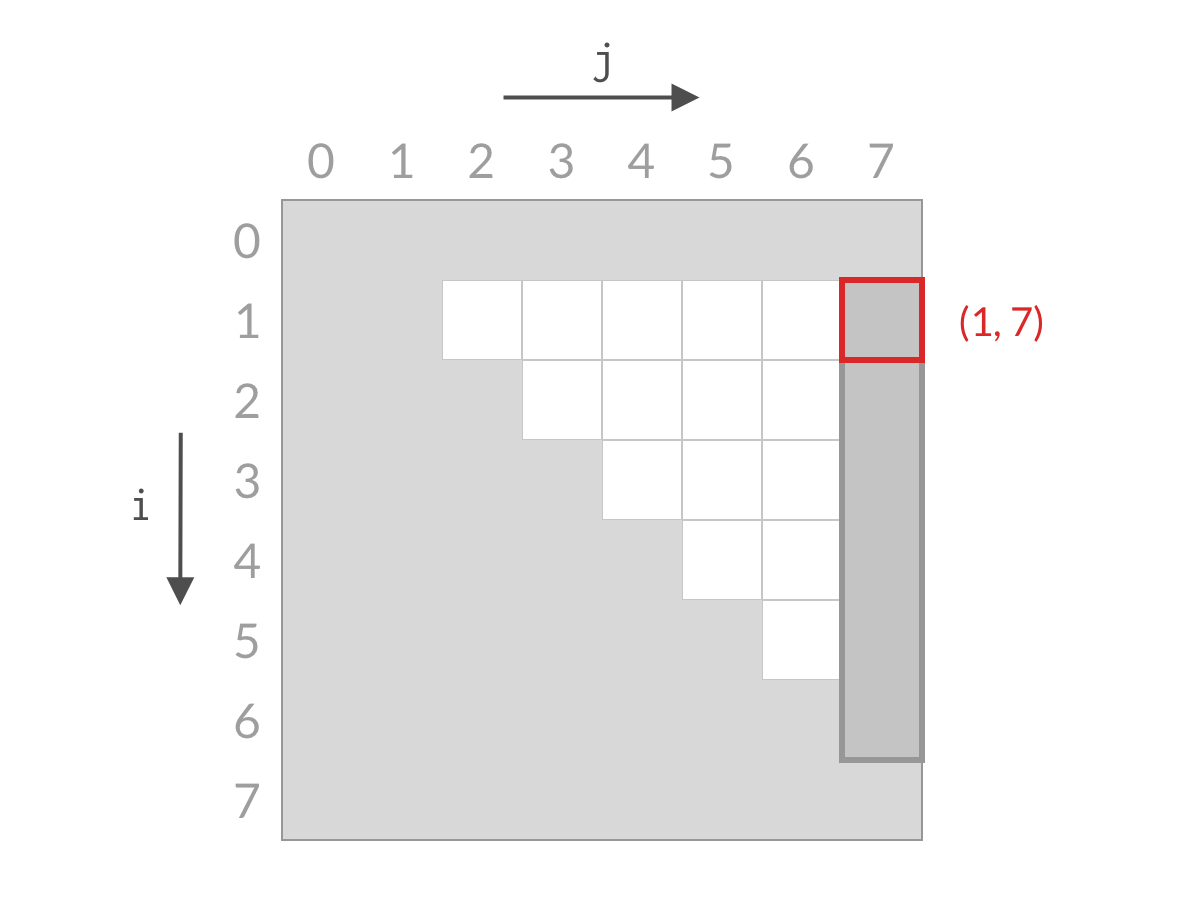
可以看到,无论柱子 i 和 j 哪根更长,我们都可以排除掉一行或者一列的搜索空间。经过 n 步以后,就能排除所有的搜索空间,检查完所有的可能性。搜索空间的减小过程如下面动图所示:
代码实现:

可以看到,无论柱子 i 和 j 哪根更长,我们都可以排除掉一行或者一列的搜索空间。经过 n 步以后,就能排除所有的搜索空间,检查完所有的可能性。搜索空间的减小过程如下面动图所示:

代码实现:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MIN(x,y) (x<y?x:y)
int maxArea(int *height, int heightSize){
int left=0;
int right=heightSize-1;
int max_area=0;
while(left<right){
int high=MIN(height[left], height[right]);
int wide=right-left;
int area=high*wide;
max_area=area>max_area?area:max_area;
if(height[left]<height[right]){
left++;
}else{
right--;
}
}
return max_area;
}
实际上还有几道题也是用到了这样的缩减搜索空间的思想:
167. Two Sum II - Input array is sorted
240. Search a 2D Matrix II
如果你觉得本文对你有帮助,欢迎关注我的公众号《面向大象编程》,其中的《LeetCode 例题精讲》系列文章正在写作,不仅有题解,更能让你学会解题的通用思路,举一反三!
作者:nettee
链接:https://leetcode-cn.com/problems/container-with-most-water/solution/on-shuang-zhi-zhen-jie-fa-li-jie-zheng-que-xing-tu/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
#include <stdlib.h>
#include <string.h>
#define MIN(x,y) (x<y?x:y)
int maxArea(int *height, int heightSize){
int left=0;
int right=heightSize-1;
int max_area=0;
while(left<right){
int high=MIN(height[left], height[right]);
int wide=right-left;
int area=high*wide;
max_area=area>max_area?area:max_area;
if(height[left]<height[right]){
left++;
}else{
right--;
}
}
return max_area;
}
实际上还有几道题也是用到了这样的缩减搜索空间的思想:
167. Two Sum II - Input array is sorted
240. Search a 2D Matrix II
如果你觉得本文对你有帮助,欢迎关注我的公众号《面向大象编程》,其中的《LeetCode 例题精讲》系列文章正在写作,不仅有题解,更能让你学会解题的通用思路,举一反三!
作者:nettee
链接:https://leetcode-cn.com/problems/container-with-most-water/solution/on-shuang-zhi-zhen-jie-fa-li-jie-zheng-que-xing-tu/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/container-with-most-water
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
以上是关于盛最多水的容器的主要内容,如果未能解决你的问题,请参考以下文章