最近公共祖先

Posted 2020-11-26 cutepota

tarjan算法：离线处理询问，核心思想是并查集。 如该图，现有4个询问：6-7，6-9，7-10，2-11

 

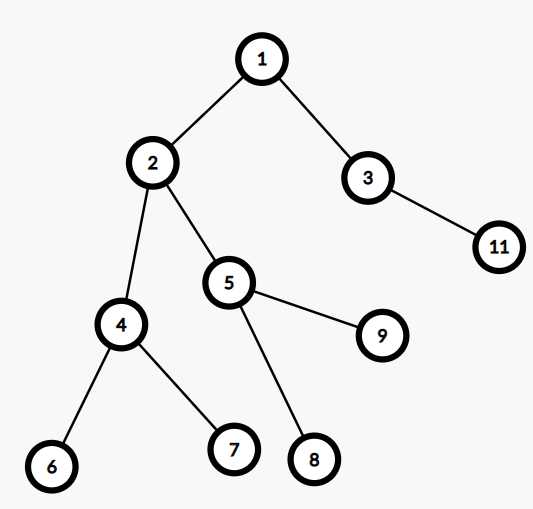
实现：1.先把询问数翻倍，除了本身的询问，还要增加两个点反过来的询问，即7-6，9-6，10-7，11-2。为什么要这样？因为在询问时，不知道两个点的先后顺序。

2.从根结点出发，做dfs遍历，遍历到第一个叶子结点时开始回退。每个结点回退前，查询该点有无询问，有则处理。回退时，进行并查集的合并操作。如上图，从1开始遍历，1-2-4-6，6准备回退前，查询有无6的询问，有6-7，6-9，看另一点是否访问，7和9均未访问，回退，1-2-4-6-4，此时fa（6）=4，继续遍历与4连接的点，1-2-4-6-4-7，此时查找有无关于7的询问，查询到7-6，6已访问，此时fa（6）=4，4即为7-6的最近公共祖先。fa（7）=4，继续回退，1-2-4-6-4-7-4，......，1-2-4-6-4-7-4-2-5-8-5-9，遍历到9时，回退前查询询问，有关于9的询问，9-6，此时6已遍历，查6此时的父亲点2即为9-6的最近公共祖先。

代码如下：

 1 #include <vector>
 2 #include <cstdio>
 3 using namespace std;
 4 inline int read()
 5 {
 6     int x = 0, f = 0;
 7     char c = getchar();
 8     for (; c < ‘0‘ || c > ‘9‘; c = getchar()) if (c == ‘-‘) f = 1;
 9     for (; c >= ‘0‘ && c <= ‘9‘; c = getchar()) x = (x << 1) + (x << 3) + (c ^ ‘0‘);
10     return f ? -x : x;
11 }
12 
13 const int N = 5e5 + 7;
14 
15 int n, m, u, v, s;
16 int tot = 0, st[N], to[N << 1], nx[N << 1], fa[N], ans[N], vis[N];
17 struct note { int node, id; }; //询问以结构体形式保存
18 vector<note> ques[N];
19 
20 inline void add(int u, int v) 
21 { to[++tot] = v, nx[tot] = st[u], st[u] = tot; 
22 }
23 inline int getfa(int x) 
24 { return fa[x] == x ? x : fa[x] = getfa(fa[x]); } 
25 //并查集的getfa操作，路径压缩
26 
27 void dfs(int u, int from)
28 //u代表目前所在的点,from代表u的父亲点 
29 {
30     for (int i = st[u]; i; i = nx[i]) //遍历与u相连的所有的边 
31          if (to[i] != from) 
32              dfs(to[i], u), fa[to[i]] = u; //将u的儿子合并到u
33     int len = ques[u].size(); //处理与u有关的询问
34     for (int i = 0; i < len; i++) 
35     if (vis[ques[u][i].node]) 
36          ans[ques[u][i].id] = getfa(ques[u][i].node); 
37     //处理与u相关的第i个询问，如果对应的v已访问 
38     //找此时v的father，即为u，v的最近公共祖先 
39     vis[u] = 1; //访问完毕回溯
40 }
41 
42 int main()
43 {
44     n = read(), m = read(), s = read();
45     //n个点，m条询问，s为root 
46     for (int i = 1; i < n; i++) //n-1条边 
47     u = read(), v = read(), 
48     add(u, v), add(v, u);
49     for (int i = 1; i <= m; i++)  //m个询问 
50     u = read(), v = read(), 
51     ques[u].push_back((note){v, i}), 
52     ques[v].push_back((note){u, i}); 
53     //记下询问编号便于输出
54     for (int i = 1; i <= n; i++) 
55           fa[i] = i;
56     dfs(s, 0); //从s出发，访问 
57     for (int i = 1; i <= m; i++) 
58     printf("%d
", ans[i]); //输出答案
59     return 0;
60 }