梯度下降法以及实现

Posted 2020-11-26 xiuercui

1.梯度下降的场景假设：

假如你想从山顶下山，但是迷雾重重，你看不清楚前方的路，假设你每一步走的距离是一样的，你想要尽快下山，那么你该怎么走？

这个问题就相当于梯度下降，每走一步，直接找坡度最大的方向，在步长一定的情况下，下降的高度是最多的，所以下山最快。

这里坡度最大的方向其实就是梯度下降的方向。

2.梯度下降法使用的场景

在机器学习中，其实我们主要的目的一直都是建模，将误差，损失降到最小，那就会有损失函数，就是求损失函数的最小值，也就是上边所说的到达山底，主要运用到特征值比较多的情况下，因为我们也知道损失函数直接求导等于0就可以得到最小值，但是当特征值多的时候，计算太过繁琐，复杂度太大，所以我们选用梯度下降法，比较简单，得到一个近似值。

3.梯度下降的相关概念

（1）步长（Learning rate）：步长决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度。用上面下山的例子，步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。

（2）特征（feature）：指的是样本中输入部分，比如2个单特征的样本（x(0),y(0)）,（x(1),y(1)）（x(0),y(0)）,（x(1),y(1)）,则第一个样本特征为x(0)x(0)，第一个样本输出为y(0)y(0)。

（3）假设函数（hypothesis function）：在监督学习中，为了拟合输入样本，而使用的假设函数，记为hθ(x)hθ(x)。比如对于单个特征的m个样本（x(i),y(i)）(i=1,2,...m)（x(i),y(i)）(i=1,2,...m),可以采用拟合函数如下：假设函数（hypothesis function）：在监督学习中，为了拟合输入样本，而使用的假设函数，记为hθ(x)hθ(x)。比如对于单个特征的m个样本（x(i),y(i)）(i=1,2,...m)（x(i),y(i)）(i=1,2,...m),可以采用拟合函数如下：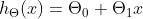

（4）损失函数（loss function）：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平方（最小二乘法）。比如对于m个样本（xi,yi）(i=1,2,...m)（xi,yi）(i=1,2,...m),采用线性回归，损失函数为：

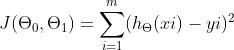
4.梯度下降具体使用

# 导包
import numpy as np

import matplotlib.pyplot as plt
%matplotlib inline

# 定义函数，也就是损失函数
f = lambda x : (x - 3)**2 + 2.5*x -7.5

# 求解导数令导数等于0求解最小值
2*(x - 3)*1 + 2.5 = 0
2*x - 3.5 = 0
x = 1.75

# 画出函数图
x = np.linspace(-2,5,100)

y = f(x)

plt.plot(x,y)

# 梯度下降求解最小值
# 导数函数
d = lambda x : 2*(x - 3) + 2.5

# 学习率，每次改变数值的时候，改变多少，就是步长
learning_rate = 0.1

# min_value瞎蒙的值，方法，就是个初始值，最快的速度找到最优解（梯度下降）
min_value = np.random.randint(-3,5,size = 1)[0]
print(‘-------------------‘,min_value)
# 记录数据更新了，原来的值，上一步的值,退出条件，其实就是保证下边死循环的时候第一步不退出
min_value_last = min_value + 0.1
# tollerence容忍度，误差，在万分之一，任务结束
tol = 0.0001
count = 0
while True:
    if np.abs(min_value - min_value_last) < tol:
        break
#梯度下降
    min_value_last = min_value
#更新值:梯度下降
    min_value = min_value - learning_rate*d(min_value)
    count +=1
    print(‘+++++++++++++++++++++%d‘%(count),min_value)
print(‘**********************‘,min_value)

5.梯度上升

# 定义函数
f2 = lambda x : -(x - 3)**2 + 2.5*x -7.5

x = np.linspace(-2,10,100)
y = f2(x)
plt.plot(x,y)

# 梯度提升 导数函数
result = []
d2 = lambda x : -2*(x - 3) + 2.5
learning_rate = 10
# max_value瞎蒙的值，方法，最快的速度找到最优解（梯度下降）
# 梯度消失，梯度爆炸（因为学习率太大）
max_value = np.random.randint(2,8,size = 1)[0]
# max_value = 1000

result.append(max_value)

print(‘-------------------‘,max_value)
# 记录数据更新了，原来的值，上一步的值,退出条件
max_value_last = max_value + 0.001
# tollerence容忍度，误差，在万分之一，任务结束
# precision精确度，精度达到了万分之一，任务结束
precision = 0.0001
count = 0
while True:
    if count >3000:
        break
    if np.abs(max_value - max_value_last) < precision:
        break
#     梯度上升
    max_value_last = max_value
#     更新值:梯度上升
    max_value = max_value + learning_rate*d2(max_value)
    result.append(max_value)
    count +=1
    print(‘+++++++++++++++++++++%d‘%(count),max_value)
print(‘**********************‘,max_value)

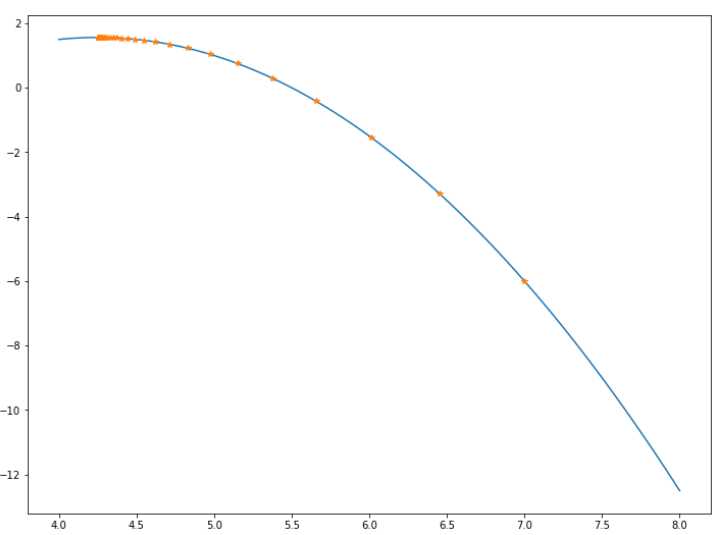
# 观察一下变化
plt.figure(figsize=(12,9))
x = np.linspace(4,8,100)
y = f2(x)
plt.plot(x,y)
result = np.asarray(result)
plt.plot(result,f2(result),‘*‘)

最后一个图

6.梯度消失和梯度爆炸(神经网络训练中会出现)

这里只是简单参考

梯度爆炸的原因：

梯度爆炸一般出现在深层网络和权值初始化比较大的情况下，其实就是学习率太大，步长太大，比如即将到达山底，结果步长太大，就会越来越大，不是越来越小.